
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Статистическое определение вероятности
|
|
Будем фиксировать число испытаний, в результате которых появилось некоторое событие А. Пусть было проведено N испытаний, в результате которых событие А появилось ровно nN раз. Тогда число nN называется частотой события, а отношение nN \ N - частyостью (относительной частотой) события.
Замечательным экспериментальным фактом является то, что частyость события при большом числе повторений испытания начинает мало изменяться и стабилизируется около некоторого определенного значения, в то время как при малом числе повторений она принимает различные, совершенно случайные значения. Поэтому интуитивно ясно, что если при неограниченном повторении испытания частyость события будет стремиться к вполне определенному числовому значению, то это значение можно принять и качестве объективной характеристики события А. Такое число Р(А), связанное с событием А, называется вероятностью события А.
Математически неограниченное число повторений испытания записывается в виде предела (lim) при N, стремящемся к бесконечности (∞): P(A) = limn->∞ nN\N.
Поскольку nN никогда не может превзойти N, то вероятность оказывается заключенной в интервале 0≤P(A)≤1.
Следует отметить, что приведенное определение вероятности является абстрактным, оно не может быть экспериментально проверено, так как на практике нельзя реализовать бесконечно большое число повторений испытания.
Пусть проводятся независимые испытания, при каждом из которых вероятность события А неизменна. Справедливо утверждение, называемое законом больших чисел или теоремой Бернулли: если N достаточно велико, то с вероятностью сколь угодно близкой к единице, отличие nN\N от Р(А) меньше любого наперед заданного положительного числа или, в символьной записи, p(| nN\N-P(A)|>G)=1. (G-сигма) Т.е. много раз бросая монету, мы “почти наверняка” будем получать примерно равные частоты выпадения герба и цифры.
Вопрос 6 Совместные и несовместные события.
События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий. Р(А+В)=р(А)+р(В)
Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
р(А)+р(не А)=1
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. р(А+В)=Р(а)+р(В)-р(А и В)
Формула умножения вероятностей
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место. Для совместных, зависимых событий: P(AB) = P(A)×P(B/A) = P(B)×P(A/B).
для несовместных, независимых: P(AB) = P(A)×P(B).
Вопрос 7 Правило исчисления теоретико-множественной суммы событий.
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий. Р(А+В)=р(А)+р(В)
Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице. р(А)+р(не А)=1
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. р(А+В)=Р(а)+р(В)-р(А и В).
Вопрос8 Теорема сложения вероятностей.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е. если AB=0, то P(A+B)=P(A)+P(B).
Доказательство: Пусть n-общее число всех возможных и равновозможных элементарных исходов испытания m 1 сумме вероятностей благоприпятствующих событию А, а m 2 событию B. Т.к. событие А и В несовместны, то появление события А исключает появление события В и обратно; следовательно число благоприятных исходов события А+В равно m 1+ m 2, т.о.:P(A+B)= m 1+ m 2\ n= m 1\ n + m 2\ n=P(A)+P(B).
Пример: В урне 2 белых 3красных и 5 синих шаров. Какова вероятность, что шар, случайным образом извлечём из урны будет цветным(не белым)? Пусть А-событие при извлечении красного шара из урны, а событие В-извлечение синего шара. Тогда А+В-извлечение цветного шара из урны. Итак,
1) n=10; 2)случайным выбором } =>P(A)=m \ n
3)выбираем не белый шар; 4) m 1 =3 , m 2 =5; 5)P(A)=3 \ 10, P(B)=3 \ 5; 6) P(A+B)=P(A)+P(B)=3 \ 5+3 \ 10=0,8
Вопрос 9 Условная вероятность.
Вероятность события А при условии, что произошло событие В называется условной вероятностью события А и обозначается: P(A \ B)=P B (A).
Пример: В урне 7 белых и 3 черных шара. Какова вероятность:1)извлечение из урны белого шара(событие А); 2)извлечение из урны белого шара после удаления из неё одного шара, который является белым(событие В) или чёрным (событие С). P(A)=7 \ 10; P B (A)=6 \ 9; P c (A)=7 \ 9.
Вопрос 10 Независимые и зависимые события.
Два события А и В называется независимыми, если вероятность каждого из них не зависит от появления или не появления другого, т.е. P(A)=P B (A)=P B-- (A);и P(B)=P A (B)=P A --(B). В противном случае событие называется зависимым.
Вопрос 11 Правило исчисления теоретико-множественной произведения событий.
Формула умножения вероятностей
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место. Для совместных, зависимых событий: P(AB) = P(A)×P(B/A) = P(B)×P(A/B).
для несовместных, независимых: P(AB) = P(A)×P(B)
Вопрос 12 Теорема умножения вероятностей.
Вероятность произведения двух событий А и В равна произведению вероятности одного из них на условную вероятность другого в предположении, что первое событие произошло: P(A*B)=P(A)*P A (B).
Вопрос 13 Формула полной вероятности.
P(A)=P(B 1)*P B1 (A)+P(B 2)*P B2 (A)+….+P(B n)*P Bn (A).
Вопрос 14 Формула Байеса.
Условная вероятность — вероятность одного события при условии, что другое событие уже произошло. В некоторых случаях ее можно рассчитать, используя формулу Байеса.
Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H1, H2,..., Hn, образующих полную группу. Событие A уже произошло. Требуется вычислить условные вероятности гипотез (при условии, что событие А произошло).
Формула Байеса P(A|B)=P(B|A)*P(A)\P(B), где P(A).
Вопрос 15 Случайная величина как функция от элементарных исходов опыта.
Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной величины образуют множество, которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z.
В зависимости от вида множества случайные величины могут быть дискретными и недискретными. СВ Х называется дискретной, если множество ее возможных значений - счетное или конечное. Если множество возможных значений СВ несчетно, то такая СВ является недискретной.
В теоретико-множественной трактовке основных понятий теории вероятностей случайная величина Х есть функция элементарного события: X=φ(ω), где ω - элементарное событие, принадлежащее пространству Ω. При этом множество Ξ возможных значений СВ Х состоит из всех значений, которые принимает функция φ(ω).
Вопрос 16 Функция распределения случайной величины.
Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x: F(x)=P{X<x}.
Функция распределения любой случайной величины обладает следующими свойствами: 1) F(x) определена на всей числовой прямой R; 2) F(x) не убывает, т.е. если x1 ≤ x2, то F(x1) ≤ F(x2); 3) F(-∞)=0, F(+∞)=1, т.е. lim x →-∞F(x)=0 и lim x →+∞F(x)=1; 4) F(x) непрерывна справа, т.е. lim x→x0+0 F(x)=F(x 0).
Вопрос 17 Дискретные случайные величины. = Вопрос 18 Непрерывные случайные величины.
Дискретные СВ принимают в результате испытания одно из изолированного дискретного множества значений. Они хорошо подходят для описания результатов значений, связанных с подсчётом и выражаемых целыми числами. (счётное и конечное значение). Вероятность принятия дискретной СВ каждого из возможных её значений больше нуля. P(x;xi);Pi, где i=..-1,0,1..(-∞;+∞). Непрерывные СВ в результате испытания могут принимать любые значения из некоторого интервала. Поскольку число возможных значений непрерывной СВ бесконечно велико и чаще всего нет оснований предположить, что одни значения появляются чаще других, то вероятность принятия непрерывной СВ каждого отдельного значения равна нулю. По этой причине нельзя описать распределение непрерывной СВ в виде вероятностей её отдельных значений.
Вопрос 19 Функция плотностей распределения вероятностей.
Плотность вероятностей – это производная от функции распределения непрерывной СВ т.е. f(x)=df(x) \ dx. Вероятность попадания непрерывной СВ в интервале между значениями х 1 и х 2 пропорциональная площади под кривой плотности вероятностей, заключенной между точками х 1 и х 2. Эта вероятность математически записывается в виде интервала от f(x) в пределах х 1 и х 2. p(х 1≤ X≤ х 2)=∫х 2 х 1 f(x)dx. Свойства f(x): 1) f(x)≥0; 2) f(x)=0, при х<x min; 3) f(x)=0, при х>x max.; 4) ∫+∞-∞ f(x)dx=1.
Вопрос 20 - Последовательности испытаний.
Если события независимы, то последовательность независимых испытаний называют схемой независимых испытаний или полиномиальной схемой, частным случаем которой (испытания с двумя исходами) является схема Бернулли.
Последовательностью независимых испытаний называется конечная вероятностная схема, в которой вероятности элементарных событий определяется формулой: P(ω)=P х1 P х2.. P хn, как произведение вероятностей исходов отдельных испытаний.
Пусть проводится конечное число n последовательных испытаний, в каждом из которых некоторое событие A может либо наступить (успех) либо не наступить (неудача), причём эти испытания удовлетворяют следующим условиям:
1) каждое испытание случайно относительно события A, т. е. до проведения испытания нельзя сказать, появится A или нет;
2) испытания проводятся в одинаковых, с вероятностной точки зрения, условиях, т. е. вероятность успеха в каждом отдельно взятом испытании равна P и не меняется от испытания к испытанию;
3) испытания независимы, т. е. события A1,A2,K,A n, где A i состоит в успехе на i-м испытании (i=1,2,..,n), независимы в совокупности. Такая последовательность испытаний называются схемой Бернулли или биномиальной схемой, а сами испытания - испытаниями Бернулли.
4) вероятность наступления определенного события А одна и та же и равна Р.
последовательность испытания Бернулли. P(A)=P; P(A -)=q=1-p.
Вопрос 21 Случайная величина Бернули.
Случайная величина Х имеет распределение Бернули, если она принимает всего 2 значения 1 и 0 с вероятностями p и q=1-р соответственно. Таким образом: P(x=1)=p; P(x=0)=q. Принято говорить, что событие {x=1} соответствует успеху, а {x=0} – неудаче. (P n (m)=C nm p m q n-m), где n – число испытаний в серии; m - случайная величина(число появления числа А); P n (m) – вероятность того, что А произойдёт именно m раз; q=1-p (вероятность того, что m не появится в испытании).
Вопрос 22 Схема независимых испытаний Бернули.
n – количество испытаний; p – успех; q=1-p – неудача; k – количество успехов. (P n (k)=C nk *p k *q n-k ).
Вопрос 23 Биноминальная случайная вероятность.
Биноминальное распределение. Дискретная случайная величина Х имеет биноминальное распределение, если её закон распределения описывается формулой Бернулли: P(X=K)=P(n,k)=C nk p k q n-k. На практике биноминальное распределение возникает при следующих условиях; Пусть проводится серия из n-испытаний, в каждом из которых некоторое событие появляется с вероятностью p. Случайная величина Х, равная числу наступлений события в n-опытах, имеет биноминальное распределение MX=n; DX=npq. Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона: (p+q) n =C nk p 0 q n +C n1 pq n-1 +..+C nk p k q n-k +C nm p n q 0 =1; p+q=1 т.е. Σ nk=0 P n (k)= Σ nk=0 C nk p k q n-k =1.
Дискретная случайная величина, принимающие любые целые неотрицательные значения от 0 до n с вероятностями C nk p k q n-k называется биноминальной случайной величиной.
Вопрос 24 Локальная предельная и интегральная теорема Муавра-Лапласа.
Применяются в случае, когда p и q не малы, а npq>9. Локальная. Если вероятность появляния события А в каждом из n (n→∞) независимых испытаний равна одной и той же постоянной p=const (0<p<1) то вероятность p(n,k) того, что во всех этих испытаниях событие А появится ровно k-раз, приближен, но вычисляется формулой: P(n,k)=1 \ √npq * φ(x), где х=k-np \ √npq; φ(x)= 1 \ √2п е- х2\2 – кривая Гаусса.
Интегральная. Пусть вероятность появления события А в каждом из n(n→∞) независимых испытаний равна одной и той же постоянной p(0<p<1), то вероятность Р(n,k) того, что во всех этих испытаниях событие А появится не менее k 1 раз и не более k 2 раз, приближённо вычисляется формулой: P(n, k1≤k≤ k 2) (Ф(х 2) - Ф(х 1)), где Ф(х) = 2 \ √2п ∫ 0х ехр(- х 2\ 2)dx.- формула Лапласа. Х 1 =k 1 -np \ √npq; x 2 =k 2 -np \ √npq. (p(k 1 ≤x≤k 2)=∫ u1u2 f(u)du).
Вопрос 25 Предельная теорема Пуассона и случайная величина Пуассона.
Распределение Пуассона. Соотношениями, описывающими биноминальное распределение, удобно пользоваться в тех случаях, если величина и достаточно мала, а р велико.
Теорема: Если, n→∞, а p→0 так, что np=a(0<a<∞), то P{X=k}=C nk p k q n-k =a k\ k! * e -a при любом k=0,1,…. Числовые характеристики: М[Х] = α, D[X] = α. Закон Пуассона зависит от одного параметра α, смысл которого заключается в следующем: он является одновременно и математическим ожиданием и дисперсией случайной величины Х.
Вопрос 26 Предельные теоремы Муавра-Лапласа и случайная величина Гаусса.
Пусть событие 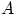 может произойти в любом из n независимых испытаний с одной и той же вероятностью P и пусть V n (А)- числоосуществлений события А в n испытаниях. Тогда V n (А)-np \ √np(1-p)=> N 0,1 при n→∞, т.е. для любых вещественных x<y имеет место сходимость P(x≤ V n (А)-np \ √np(1-p)≤y)→Ф 0,1 (y)- Ф 0,1 (x)=∫ xy 1 \ √2п *e-t 2 / 2 dt.
может произойти в любом из n независимых испытаний с одной и той же вероятностью P и пусть V n (А)- числоосуществлений события А в n испытаниях. Тогда V n (А)-np \ √np(1-p)=> N 0,1 при n→∞, т.е. для любых вещественных x<y имеет место сходимость P(x≤ V n (А)-np \ √np(1-p)≤y)→Ф 0,1 (y)- Ф 0,1 (x)=∫ xy 1 \ √2п *e-t 2 / 2 dt.
Доказательство. Величина V n (A) есть сумма независимых, одинаково распределённых случайных величин, имеющих распределение Бернули с параметром, равным вероятности успеха р: V n (A)=ξ 1 +…+ ξ n, где ξ i =I i (A)={1, если А произошло в i-м испытании; 0, если А не произошло в i-м испытании. Еξ 1 =р, Dξ 1 =p(1-p). Нормальный закон распределения (закон Гаусса). Плотность вероятности нормально распределённой случайной величины X выражается формулой φ(х)=1\√2п * е – х2\2.
Нормальный закон распределения широко применяется в задачах практики. Объяснить причины этого впервые удалось Ляпунову. Он показал, что если случайная величина может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. А так как практически случайные величины в большинстве случаев бывают результатом действия множества причин, то нормальный закон оказывается наиболее распространённым законом распределения. Укажем числовые характеристики нормально распределённой случайной величины (математическое ожидание и дисперсия): M(X)=a; D[X]= σ 2. Характеристическая функция нормального распределения случайной величины задаётся формулой g(s)=exp(ias-1\σ 2 s 2).
Вопрос 27 Равномерное и нормальное распределения.
Нормальное распределение. Нормальное распределение вероятностей особенно часто используется в статистике. Нормальное распределение дает хорошую модель для реальных явлений, в которых: 1) имеется сильная тенденция данных группироваться вокруг центра; 2) положительные и отрицательные отклонения от центра равновероятны; 3) частота отклонений быстро падает, когда отклонения от центра становятся большими.
Идея состоит в том, что при суммировании большого числа независимых величин в определенных разумных условиях получаются именно нормально распределенные величины. И это происходит независимо, то есть инвариантно, от распределения исходных величин. Иными словами, если на некоторую переменную воздействует множество факторов, эти воздействия независимы, относительно малы и слагаются друг с другом, то получаемая в итоге величина имеет нормальное распределение.
Формально плотность нормального распределения записывается так: φ(x,a,σ 2)=1\√2п σ * e (- (x-a)2\2σ2) (-(x-a) 2 \2σ 2), где а и σ 2 - параметры закона, интерпретируемые соответственно как среднее значение и дисперсия данной случайной величины (ввиду особой роли нормального распределения мы будем использовать специальную символику для обозначения его функции плотности и функции распределения).
Равномерное распределение. Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение (f(x) = const при a ≤ x ≤ b, f(x) = 0 при x < a, x > b.
Из условия нормировки следует, что ∫ ab f(x)dx=∫ ab cdx=c(b-a)=1, откуда f(x)=c=1\b-a. Вероятность попадания равномерно распределенной случайной величины равна при этом ∫ αβ 1\b-a dx=β-α\b-a.Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.
Ниже приведены формулы плотности и функции распределения равномерной случайной величины, принимающей значения на отрезке [а, b]. f ξ (x)= {1\b-a, при а≤х≤b; 0, при x<а и b>x/. F ξ (x)={0, при x≤a; x-a\b-a, при a<x≤b; 1, при b>x. Из этих формул легко понять, что вероятность того, что равномерная случайная величина примет значения из множества [с, d] [а, b], равна (d — c)/(b — a).
Вопрос 28 Предельные теоремы о связи биномиальной и случайной величины со случайными величинами Пуассона и Гаусса (предельная теорема Пуассона в схеме Бернулли, локальная и интегральная теоремы Муавра - Лапласа).
Теорема Пуассона в схеме Бернулли. При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 0,97 999 вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона: P n (k)=ᴧ k \k! *e -ᴧ,ᴧ=np (ᴧ-лямбда) – среднее число появлений события в n испытаниях. Эта формула дает удовлетворительное приближение для p<=0,1 и np<=10. При больших np рекомендуется применять формулы Лапласа (Муавра-Лапласа). События, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).Пусть P n - вероятность успеха в серии из n испытаний и при и n→∞ np n =ᴧ - остается постоянным. Тогда P n (k)→e -ᴧ ᴧ k \k!
Локальная формула Лапласа. Пусть в каждом из n независимых испытаний событие A может произойти с вероятностью P, q=1-p.Обозначим как и раньше, через P n (k) вероятность ровно k появлений события А в n испытаниях. кроме того, пусть P n (k 1;k 2) вероятность того, что число появлений события А находится между k1 и k2. Локальная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то P n (k)≈1\√npq φ(k-np\√npq), где φ(x)=1\√2п *e x2\2 - функция Гаусса.
Интегральная формула Муавра-Лапласа. Пусть в каждом из n независимых испытаний событие A может произойти с вероятностью P, q=1-p.Обозначим как и раньше, через P n (k) вероятность ровно k появлений события А в n испытаниях. кроме того, пусть P n (k 1;k 2)– вероятность того, что число появлений события А находится между k1 и k2. Интегральная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то P(n; k1, k2) P n (k 1;k 2)≈φ(k 2 -np\√npq)-φ(k 1 -np\√npq), где φ(x)=1\√2п ∫ ax e -t2\2 dt - функция Лапласа.
Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций: а) φ(-x)= φ(x),Ф(-х)=-Ф(х) б) при больших x верно φ(х)≈0, Ф(х)≈0,5. Теоремы Лапласа дают удовлетворительное приближение при npq>=9. Причем чем ближе значения q,p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).
Вопрос 29 Правило «три сигма» для нормальной случайной величины.
Вероятность того, что случайная величина отклонится от своего математического ожидания на большую величину, чем утроенное среднее квадратичное отклонение, практически равна нулю. Правило справедливо только для случайных величин, распределенных по нормальному закону. Например, пусть имеется выборка наблюдений за ежедневными продажами в магазине. Значения их распределены по нормальному закону с математическим ожиданием 150000 руб. и среднеквадратическим отклонением 20000 руб. Тогда в соответствии с правилом 3-х сигм продажи ниже, чем 150 000 - 20 000 x 3 = 90 000, и выше, чем 150 000 + 20 000 х 3 = 210 000, являются практически невозможными событиями. Фактически это означает, что рассматривать данные объемы продаж как потенциально возможные не имеет смысла.
Вопрос 30 таблица стандартного нормального распределения.
Нормальное распределение, также называется гауссовым распределением или распределением Гаусса – распределение вероятностей, которое задаётся функцией плотности распределения: φ(х)=1\√2п *е х2\2. В следующей таблице приведены значения функции стандартного нормального распределения Φ(х) для значений аргумента в интервале от 0 до 4 с шагом 0.01. Каждый элемент матрицы представляет значение функции Φ в точке x, равной сумме заголовков строки и столбца. Например, для нахождения значения Φ в точке 0.26, достаточно взять число из строки 0.2 и столбца 0.06, то есть, Φ(0.26) = 0.6026. Аналогично, Φ(2.31) = Φ(2.3 + 0.01) = 0.9896. Для отрицательных x можно вычислить значение функции по формуле Φ(x) = 1 - Φ(-x). Например, Φ(-1.67) = 1 - Φ(1.67) = 1 - 0.9525 = 0.0475.
| 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | |
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
Date: 2015-06-05; view: 892; Нарушение авторских прав