Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Функция, заданная параметрически
|
|
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
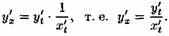
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть 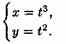
Найти у'х.
Решение: Имеем x't=3t2, y't=2t. Следовательно, у'х=2t/t2, т. е. 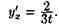
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно,  Тогда
Тогда 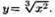 Отсюда
Отсюда 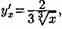 т. е.
т. е. 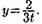
30) Дифференциал функции
Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства: 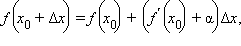 где α – бесконечно малая в окрестности
где α – бесконечно малая в окрестности 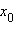 функция. Для приближенного вычисления значения функции f в точке x 0 + Δ x эту бесконечно малую функцию можно отбросить:
функция. Для приближенного вычисления значения функции f в точке x 0 + Δ x эту бесконечно малую функцию можно отбросить:
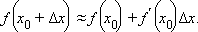
|
Линейную функцию  называют дифференциалом функции f в точке
называют дифференциалом функции f в точке 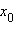 и обозначают df. Для функции x производная в каждой точке
и обозначают df. Для функции x производная в каждой точке 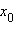 равна 1, то есть
равна 1, то есть 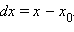 Поэтому пишут:
Поэтому пишут:
|
Приближенное значение функции вблизи точки 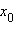 равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
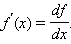
|
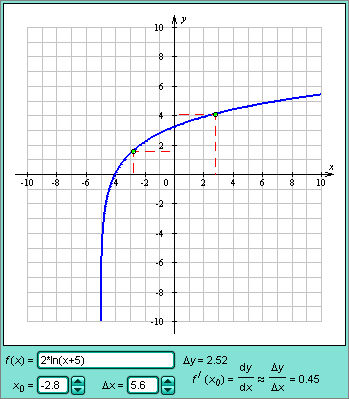
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
|
31) Исследование функции при помощи первой производной
Под интервалом мы будем подразумевать или конечный интервал, или один из
следующих числовых промежутков:, или. Заметьте, что внутри
интервала нет выколотых точек. Таким образом, если, то.
Определение 1.1. Говорят, что функция строго монотонно возрастает в интервале,
если при всех таких, что, т.е. бóльшим значениям
независимой переменной соответствуют бóльшие значения функции. Далее, строго
монотонно убывает в, если при.
В дальнейшем, говоря, что возрастает (или убывает) на, мы будем иметь в виду
возрастание (убывание) в строго монотонном смысле.
Теорема 1.2 (признак возрастания функции). Дифференцируемая функция
возрастает в интервале, если для всех.
Доказательство: Пусть и — любые две точки в такие, что. Надо
доказать, что. По теореме Лагранжа, примененной к функции на отрезке
, существует точка такая, что,
откуда, потому что и. ■
Теорема 1.3 (признак убывания функции). Дифференцируемая функция убывает в
интервале, если для всех.
Доказательство: Аналогично доказательству предыдущей теоремы. ■
Пример 1.4. Определить промежутки возрастания и убывания функции
.
Рис. 1. Диаграмма возрастания и убывания функции.2
Решение:. Исследование представлено
диаграммой на рис. 1, где плюсы и минусы означают знаки производной, а стрелки —
возрастание или убывание данной функции на соответствующих интервалах. ■
Следствие 1.5 (признаки максимума и минимума в терминах первой производной).
Пусть — критическая точка дифференцируемой функции, т.е..
а) Если меняет знак в точке с плюса на минус, то — локальный
максимум.
б) Если меняет знак в точке с минуса на плюс, то — локальный
минимум.
в) Если не меняет знак в точке, то локального экстремума в точке не
имеет. ■
Пример 1.6. Найти локальные экстремумы функции из примера 1.4.
Решение: В силу предыдущей теоремы, из диаграммы на рис. 1 видно, что значения
и являются локальными минимумами, а локальным
32)
Формула Тейлора
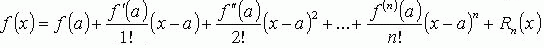
Date: 2015-06-05; view: 1323; Нарушение авторских прав