Числовые последовательности

Числовой последовательностью называется числовая функция, заданная на множестве натуральных чисел или на множестве 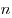первых натуральных чисел.

Для числовых последовательностей вместо 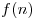обычно пишут 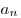, саму последовательность обозначают 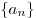, общий член последовательности обозначают 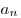. Числа 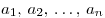называются членами последовательности: 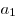— первый член последовательности, 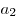— второй член последовательности, 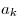— 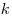-ый член последовательности и т.д.

Числовая последовательность определена, если указан закон, по которому каждому натуральному числу 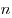ставиться в соответствие действительное число .

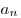Числовая последовательность может быть определена заданием ее 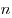-го члена формулой, позволяющей найти любой член последовательности простой подстановкой номера искомого члена в эту формулу. Такой способ задания последовательности называется явным.

Закон образования числовой последовательности может состоять в задании нескольких первых членов последовательности и рекуррентной формулы, с помощью которой каждый следующий член выражается через предыдущий (или несколько предыдущих). Такой способ задания последовательности называется рекуррентным.

Числовая последовательность называется возрастающей, если в ней каждый следующий член больше предыдущего.

Числовая последовательность называется убывающей, если в ней каждый следующий член меньше предыдущего.

Числовая последовательность называется ограниченной, если существует такое натуральное числ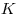о , что для любого натурального .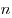

ПредеЕсли каждому натуральному числу n поставлено в соответствие некоторое вещественное число 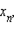то говорят, что задана числовая последовательность 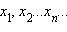Кратко она обозначается символом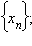 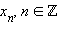называют n-м членом последовательности. Совокупность этих чисел называют множеством значений последовательности.

Существует несколько способов задания числовых последовательностей.

1. Последовательность может быть задана при помощи формулы, позволяющей вычислить каждый ее член по номеру (например, ).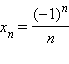

2. Часто последовательность задается при помощи рекуррентной формулы, позволяющей определить каждый член последовательности по одному или нескольким предыдущим; при этом необходимо задание одного или нескольких первых членов последовательности. К таковым относятся арифметическая и геометрическаяпрогрессии или, например, последовательность Фибоначчи, задаваемая формулой

3. и условиями x ₁ = 1, x ₂ = 1.

4. Иногда последовательность задается описанием ее членов, например, последовательность, у которой x_n равен n -му знаку после запятой в десятичной записи числаπ = 3,14159265358979323..., задается следующим образом: x ₁ = 1, x ₂ = 4, x ₃ = 1, x ₄ = 5, x ₅ = 9, x ₆ = 2, x ₇ = 6, x ₈ = 5, x ₉ = 3, x ₁₀ = 5 и т. д.

Число a называется пределом последовательности { x_n }, если для каждого ε > 0 существует такой номер N _ε, что для всех n ≥ N _ε выполняется неравенство

т. е. 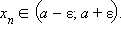При этом пишут, что 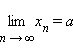или 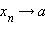при n → ∞. Кратко это определение можно записать так:

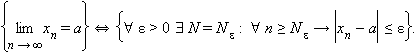
Интервал (a – ε; a + ε) называют ε-окрестностью точки a.

25) БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА

Функция y=f(x) называется бесконечно малой при x→a или при x →∞, ес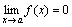ли или 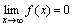, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

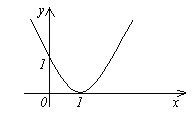
1. Функция f(x) =(x -1)² является бесконечно малой при x →1, так как 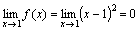(см. рис.).

2. Функция f(x) = tg x – бесконечно малая при x →0.

3. f(x) = ln (1+ x)– бесконечно малая при x →0.

4. f(x) = 1/ x – бесконечно малая при x →∞.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→a в виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Доказательство.

1. Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|< ε. Тогда |f(x) – b|< ε. А это и значит, что .

2. Если , то при любом ε >0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначим f(x) – b= α, то |α(x)|< ε, а это значит, что a – бесконечно малая.

Рассмотрим основные свойства бесконечно малых функций.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где 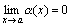и 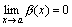. Нам нужно доказать, что при произвольном как угодно малом ε > 0 найдется δ> 0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.

Итак, зафиксируем произвольное число ε > 0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ₁ > 0, что при |x – a|< δ₁ имеем |α(x)|< ε / 2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ₂ > 0, что при |x – a|< δ₂ имеем | β(x)|< ε / 2.

Возьмем δ=min{ δ₁, δ₂ }. Тогда в окрестности точки a радиуса δ будет выполняться каждое из неравенств |α(x)|< ε / 2 и | β(x)|< ε / 2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x) | ≤ |α(x)| + | β(x)| < ε /2 + ε /2= ε,

т.е. |f(x)|< ε, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε > 0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε /M. Тогда в меньшей из этих окрестностей имеем | αf|< ε /M = ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

Из доказанной теоремы вытекают:

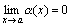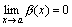Следствие 1. Если и , то .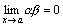

Следствие 2. Если 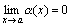и c= const, то .

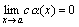Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство. Пусть 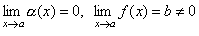. Тогда 1 /f(x) есть ограниченная функция. Поэтому дробь 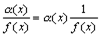есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

26)Непрерывность функции в точке

Непрерывность функции в точке.

Определение. Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

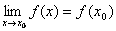
Тот же факт можно записать иначе: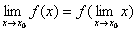

Определение. Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Функциональные ряды Примеры решения задач математика

Пример непрерывной функции:

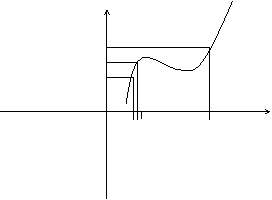y

f(x₀)+e

f(x₀)

f(x₀)-e

0 x₀-D x₀ x₀+D x

Date: 2015-06-05; view: 1042; Нарушение авторских прав