Окружность. Простейшей кривой второго порядка является окружность

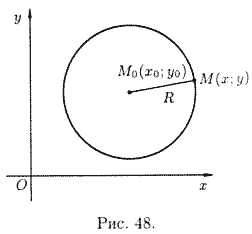Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R с центром в точке 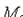называется множе­ство всех точек Μ плоскости, удовлетворяющих условию 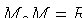. Пусть точка 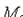в прямоугольной системе координат 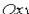имеет координаты x₀, y₀ а 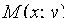— произвольная точка окружности (см. рис. 48).

Тогда из условия 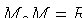получаем уравнение

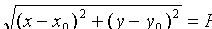, то есть

(11.2)

Уравнению (11.2) удовлетворяют координаты любой точки 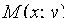данной окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.

Уравнение (11.2) называется каноническим уравнением окружности

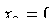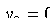В частности, полагая и , получим уравнение окружности с центром в начале координат .

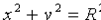Уравнение окружности (11.2) после несложных преобразований примет вид 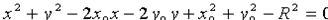. При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:

1) коэффициенты при x² и у² равны между собой;

2) отсутствует член, содержащий произведение xу текущих координат.

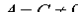Рассмотрим обратную задачу. Положив в уравнении (11.1) значения и , получим

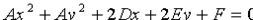(11.3)

Преобразуем это уравнение:

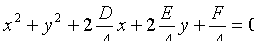
т.е.

,

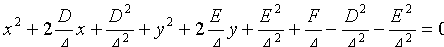т.е.

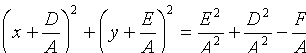
Отсюда следует, что уравнение (11.3) определяет окружность при условии 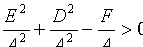. Ее центр находится в точке 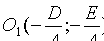, а радиус

.

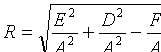Если же 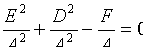, то уравнение (11.3) имеет вид

.

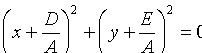Ему удовлетворяют координаты единственой точки 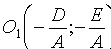. В этом случае говорят: "окружность выродилась в точку” (имеет нулевой радиус).

Если ,;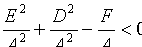

16) Уравнение плоскости в пространстве: 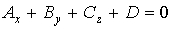- общее ур-е пл-ти в пространстве

17)Уравнение прямой в пространстве:

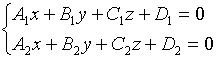- общее ур-е прямой в пространстве

18) Прямая и плоскость в пространстве.

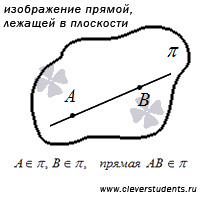
Во-первых, прямая может лежать в плоскости. В этом случае, в плоскости лежат хотя бы две точки этой прямой. Это устанавливается аксиомой: если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. Для краткой записи принадлежности некоторой прямой данной плоскости пользуются символом «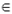». Например, запись 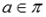означает, что прямая а лежит в плоскости .

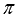Во-вторых, прямая может пересекать плоскость. При этом прямая и плоскость имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости. При краткой записи пересечение обозначаю символом «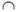». К примеру, запись 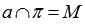означает, что прямая а пересекает плоскость 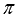в точке М. При пересечении плоскости некоторой прямой возникает понятие угла между прямой и плоскостью.

Отдельно стоит остановиться на прямой, которая пересекает плоскость и перпендикулярна любой прямой, лежащей в этой плоскости. Такую прямую называют перпендикулярной к плоскости. Для краткой записи перпендикулярности используют симовл «». Для более глубокого изучения материала можете обратиться к статье перпендикулярность прямой и плоскости.

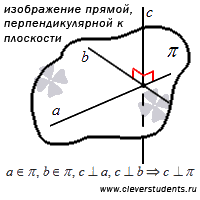
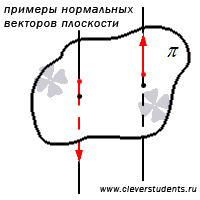
Особую значимость при решении задач, связанных с плоскостью, имеет так называемый нормальный вектор плоскости. Нормальным вектором плоскости является любой ненулевой вектор, лежащий на прямой, перпендикулярной этой плоскости.

В-третьих, прямая может быть параллельна плоскости, то есть, не иметь в ней общих точек. При краткой записи параллельности используют символ «». Например, если прямая а параллельна плоскости 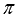, то можно записать 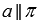. Рекомендуем подробнее изучить этот случай, обратившись к статье параллельность прямой и плоскости.

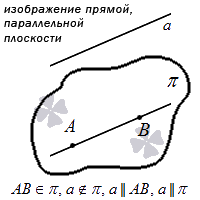
Следует сказать, что прямая, лежащая в плоскости, делит эту плоскость на две полуплоскости. Прямая в этом случае называется границей полуплоскостей. Любые две точки одной полуплоскости лежат по одну сторону от прямой, а две точки разных полуплоскостей лежат по разные стороны от граничной прямой.

рямая и плоскость в пространстве

19) Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.

Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит).
Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).

Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.

Например, перечислением заданы следующие множества:

• А={1,2,3,5,7} — множество чисел
• Х={x₁,x₂,...,x_n} — множество некоторых элементов x₁,x₂,...,x_n
• N={1,2,...,n} — множество натуральных чисел
• Z={0,±1,±2,...,±n} — множество целых чисел

Множество (-∞;+∞) называется числовой прямой, а любое число — точкой этой прямой. Пусть a — произвольная точка числовой прямой иδ — положительное число. Интервал (a-δ; a+δ) называется δ-окрестностью точки а.

Множество Х ограничено сверху (снизу), если существует такое число c, что для любого x ∈ X выполняется неравенство x≤с (x≥c). Число с в этом случае называется верхней(нижней) гранью множества Х. Множество, ограниченное и сверху и снизу, называется ограниченным. Наименьшая (наибольшая) из верхних (нижних) граней множества называется точной верхней (нижней) гранью этого множества.

Окрестность точки. 1. На числовой оси окрестность точки – любой интервал (открытый промежуток), содержащий данную точку. В частности открытый (не содержащий границ) промежуток (а – δ; а + δ) с центром в точке а называется δ-окрестностью точки а (положительное число δ – радиус δ-окрестности).
2. В n -мерном пространстве окрестность точки – любая область, содержащая данную точку. В частности совокупность точек М (х ₁; х ₂; …; х_n), координаты которых удовлетворяют неравенству
,
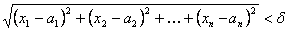называется шаровой (сферической) δ-окрестностью точки А (а ₁; а ₂; …; а_n) – окрестностью радиуса δ. Иначе говоря, указанное множество точек М образует в n -мерном пространстве (открытый) шар радиуса δ с центром в точке А.
Множество точек М (х ₁; х₂; …; х _n), координаты которых удовлетворяют системе неравенств

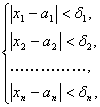
называется параллелепипедальной окрестностью точки А (а 1; а 2; …; аn). Иначе: указанное множество точек М образует в n -мерном пространстве параллелепипед с центром в точке А.
3. Окрестность точки А в метрическом пространстве – любая область, содержащая точку А. В частности все точки М, расстояние от которых до точки А меньше некоторого положительного числа δ, образуют ее (т.е. точки А) сферическую окрестность радиуса δ с центром в точке А.

20) Функции и способы их задания

Date: 2015-06-05; view: 804; Нарушение авторских прав