Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Производная. Исследование функции с помощью производной. Физический и геометрический смысл производной

⇐ ПредыдущаяСтр 8 из 22Следующая ⇒

Физический и геометрический смысл производной.

Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная 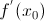– скорость изменения переменной y относительно переменной x в точке .

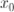Исследование функции с помощью производной.

a. ·
Найти ОДЗ и точки разрыва функции.

b. Найти точки пересечения графика функции с осями координат.

· Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.

· Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

· Найти асимптоты графика функции: а) вертикальные, b) наклонные.

· На основании проведеьнного исследования построить график функции.

 

Физический и геометрический смысл производной.

Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке


⇐ Предыдущая3456789101112Следующая ⇒





Date: 2015-06-05; view: 517; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.006 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию