Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решение. · Данная величина Х является дискретной, а ее эмпирическая функция распределения - ступенчатой
|
|
· Данная величина Х является дискретной, а ее эмпирическая функция распределения - ступенчатой. Приближенно можно представить данные обследования в следующем виде:
Таблица 1
| Выборочные значения | 1,5 | 4,5 | 7,5 | 10,5 | 13,5 | 16,5 | 19,5 | 22,5 | 25,5 | 28,5 | Итого |
| Частоты |
В качестве выборочных значений взяты середины интервалов.
Для каждого выборочного значения х найдем кумулятивную частоту nх - сумму частот для выборочных значений £ х, и эмпирическую функцию распределения
F*(x) = nx /n, где n = 100
Таблица 2
| х | 1,5 | 4,5 | 7,5 | 10,5 | 13,5 | 16,5 | 19,5 | 22,5 | 25,5 | 28,5 |
| nх | ||||||||||
| F*(х) | 0,06 | 0,15 | 0,30 | 0,49 | 0,69 | 0,83 | 0,92 | 0,97 | 0,99 |
Построим график функции F*{х), исходя из полученной таблицы 2:
 |
· пусть х1,...,х10, - выборочные значения, а n1,...,n10 - ихчастоты (из табл.1).
Найдем выборочную среднюю:
Так как значение n=100 достаточно велико, то генеральную дисперсию оценим по формуле
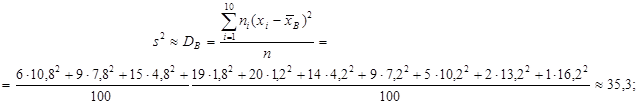откуда s» 5,9.
Задачу построения доверительного интервала решим приближенно, считая, что оценка 
распределена по нормальному закону (для этого n=100 достаточно велико).
В этом случае доверительный интервал покрывающий неизвестный параметр a =mx c вероятностью 0,95 равен
,
где значение tg ищется по таблице 3 приложений tg=t(g,n) по заданным g и n.
Имеем, tg=t(0,95,100)=1,984.
Тогда
.
Отсюда получаем доверительный интервал
.
Таким образом, в среднем в 95 случаях из 100 интервал (11,13; 13,47) накрывает среднее число поездок в месяц для случайно выбранного жителя поселка.4
3Пример 11. Выборочная проверка стоимости двухкомнатных квартир (тыс.руб.) дала следующие результаты.
| 78,0 | 76,5 | 78,5 | 83,5 | 81,0 | 84,5 | 79,0 | 87,0 | 80,5 | 78,5 |
| 83,0 | 81,0 | 80,5 | 78,0 | 83,0 | 89,0 | 89,3 | 85,0 | 82,0 | 84,0 |
| 79,0 | 82,5 | 83,0 | 79,5 | 78,5 | 79,5 | 81,1 | 89,0 | 91,0 | 83,0 |
| 84,5 | 86,0 | 84,0 | 83,0 | 84,5 | 82,5 | 87,0 | 84,5 | 85,0 | 80,5 |
| 84,0 | 83,5 | 84,5 | 85,5 | 87,0 | 83,5 | 85,0 | 78,5 | 86,0 | 82,5 |
| 82,0 | 83,0 | 80,0 | 82,0 | 79,0 | 82,5 | 87,0 | 84,0 | 85,5 | 83,0 |
Требуется:
· Составить статистическое распределение выборки.
· Разбив выборку на k классов (k=1+3,22 ×lgn), построить вариационный ряд, соответствующий этому разбиению. Построить гистограмму относительных частот.
· Вычислить для данной выборки несмещенные оценки математического ожидания, дисперсии, показателей асимметрии и эксцесса, коэффициент вариации.
· С помощью критерия Пирсона проверить гипотезу о нормальном распределении случайной величины Х – стоимости квартиры при уровне значимости a=0,05.
· Построить график плотности нормального распределения с параметрами 
и s на том же чертеже, где и гистограмма.
· Найти доверительные интервалы для математического ожидания и среднего квадратического отклонения с надежностью g=0,95.
Date: 2015-06-05; view: 1722; Нарушение авторских прав