Решение. Случайная величина Х - число полученных поставок может принимать значения: 0,1,2,3

Случайная величина Х - число полученных поставок может принимать значения: 0,1,2,3. Найдем вероятности принятия каждого из этих значений.

Обозначим через А_i (независимые события) – получение поставки товара с i-ой фирмы, где i=1,2,3, через p_i-вероятность события A_i.

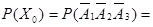| т.к. события А₁,А₂,А₃ независимы, то и события 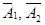, 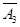независимы | 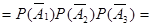(1-p₁)(1-p₂)(1-p₃)=q₁q₂q₃= (1-0,4)(1-0,3)(1-0,6)=0,168.

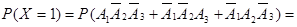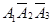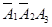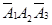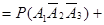
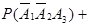
| события , , несовместны| 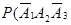)=p₁q₂q₃+q₁q₂p₃+q₁p₂q₃=

=0,4×(1-0,3)×(1-0,6)+(1-0,4)×(1-0,3)×0,6+(1-0,4)×0,3×(1-0,6)=0,436.

Р(Х=2)=Р(А₁А₂ 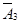)+Р(А₁ 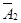А₃)+Р( 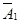А₂А₃)=р₁р₂q₃+р₁q₂р₃+q₁р₂р₃=

=0,4×0,3×(1-0,6) + 0,4×(1-0,3)×0,6+(1-0,4)×0,3×0,6=0,324.

Р(Х=3)=Р(А₁А₂А₃)=Р(А₁)×Р(А₂)×Р(А₃)=0,4×0,3×0,6=0,072.

Следовательно,

Проверим условие нормировки: .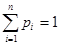

Действительно, 0,168+0,436+0,324+0,072=1.

Найдем М[X] и D[X].

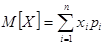=0×0,168+1×0,436+2×0,324+3×0 072=1,3.

D_x=M[X²]-m²_x = 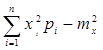=0×0,168+1×0,436+4×0,324+9×0,072-1,3² = 0,69.

s_х= 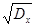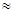0,83.

Найдем функцию распределения F(x).

Т.к. F(x)= 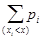, то

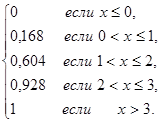F(x)= 4

Вопросы для самопроверки.

· Случайная величина. Спектр. Дискретная случайная величина.

· Закон распределения дискретной случайной величины. Условие нормировки. Многоугольник распределения.

· Функция распределения. Вероятность попадания случайной величины на промежуток и в точку.

· Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины; формулы для их нахождения.

· Биноминальное распределение и его числовые характеристики.

· Распределение Пуассона и его числовые характеристики.

Тема 4. Непрерывная случайная величина

Литература

Забейворота В.И., Волохова К.И. Математика в экономике (Теория вероятностей). Учебное пособие (параграфы 9-11). УрСЭИ, Челябинск, 2001

Законом распределения непрерывной случайной величины является плотность вероятности

f(x)=F¢(x).

Числовые характеристики непрерывной случайной величины:

математическое ожидание ,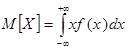

дисперсия D_x=M[X²]-m²_x= ,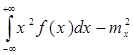

среднее квадратическое отклонение s_х= .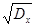

Функция распределения .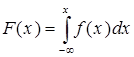

3Пример 7. Случайная величина Х – годовой доход наугад взятого лица, облагаемого налогом. Плотность распределения этой случайной величины имеет вид:

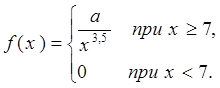
Требуется:

· определить значение параметра а,

· найти функцию распределения F(x),

· вычислить математическое ожидание m_х и среднее квадратическое отклонение 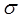_х,

· определить размер годового дохода х₁, не ниже которого с вероятностью 0,6 окажется годовой доход случайно выбранного налогоплательщика.

Date: 2015-06-05; view: 1164; Нарушение авторских прав