
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. В условиях данной задачи естественно исходить из того, что наблюдаемая случайная величина Х (дневная выручка оптовой базы) имеет непрерывное распределение
|
|
В условиях данной задачи естественно исходить из того, что наблюдаемая случайная величина Х (дневная выручка оптовой базы) имеет непрерывное распределение вероятностей.
Статистическим аналогом графика плотности распределения такой случайной величины, как известно, является гистограмма относительных частот. Она представляет собой совокупность прямоугольников, построенных на выделенных интервалах наблюденных значений случайной величины Х как на основаниях. Площадь каждого i-го прямоугольника равна относительной частоте wi i-го интервала, определяемой по формуле 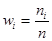 , так что
, так что 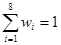 .Отсюда высота i-го прямоугольника вычисляетсякак
.Отсюда высота i-го прямоугольника вычисляетсякак 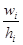 где hi, - длина i-го интервала (в нашей задаче hi = h = 5 для всех i =
где hi, - длина i-го интервала (в нашей задаче hi = h = 5 для всех i = 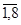 ).
).
Полная площадь гистограммы, таким образом, будет равна единице.
На основе изложенного для построения гистограммы составим следующую таблицу.
Таблица 2
| i | ||||||||
| Ji | 0-5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 - 30 | 30 - 35 | 35 - 40 |
| ni | ||||||||
| w i | 0,02 | 0,07 | 0,14 | 0,19 | 0,25 | 0,20 | 0,10 | 0,03 |
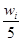
| 0,004 | 0,014 | 0,028 | 0,038 | 0,05 | 0,04 | 0,02 | 0,006 |
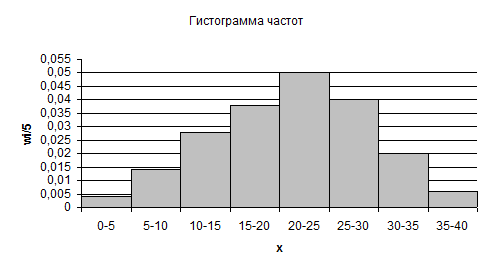 |
Построим гистограмму:
Вид этой гистограммы позволяет считать рассматриваемое распределение вероятностей нормальным.
Несмещенные оценки 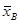 и s2 найдем по формулам
и s2 найдем по формулам
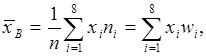
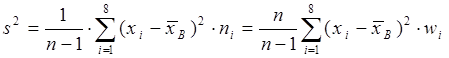 ,
,
где xi - середина i-го интервала.
Все необходимые вычисления дл я удобства и наглядности проведем в рамках следующей таблицы:
Таблица 3
| i | |||||||||||||
| xi | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 | 32,5 | 37,5 | |||||
| wi | 0,02 | 0,07 | 0,14 | 0,19 | 0,25 | 0,20 | 0,10 | 0,03 | |||||
| xi wi | 0,05 | 0,525 | 1,75 | 3,325 | 5,625 | 5,5 | 3,25 | 1,125 | |||||
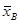 = 21,15 = 21,15
| |||||||||||||
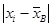
| 18,65 | 13,65 | 8,65 | 3,65 | 1,35 | 6,35 | 11,35 | 16,35 | |||||
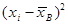
| 347,82 | 186,32 | 74,82 | 13,32 | 1,82 | 40,32 | 128,82 | 267,32 | |||||
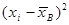 ×wi ×wi
| 6,96 | 13,04 | 10,48 | 2,53 | 0,46 | 8,06 | 12,88 | 8,02 | |||||
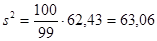
| |||||||||||||
Таким образом,
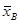 =21,15 (усл. ден. ед.)
=21,15 (усл. ден. ед.)
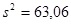 (усл. ден. ед.)2.
(усл. ден. ед.)2.
Как следует из пункта 1, распределение случайной величины Х можно считать нормальным. В качестве его параметров возьмем оценки 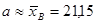 и
и 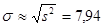 полученные в пункте 2. Тогда приближенно вероятность P(Х ³ 15) того, что в наудачу выбранный рабочий день дневная выручка оптовой базы составит не менее 15 условных денежных единиц, можно вычислить следующим образом, c использованием функции Лапласа Ф(х).
полученные в пункте 2. Тогда приближенно вероятность P(Х ³ 15) того, что в наудачу выбранный рабочий день дневная выручка оптовой базы составит не менее 15 условных денежных единиц, можно вычислить следующим образом, c использованием функции Лапласа Ф(х).
Имеем Р(x<15)+Р(x³15)=1Þ Р(x³15)=1 - Р(x<15)=1- F(15),
Но
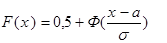 и значит
и значит 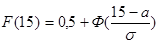
Итак, имеем
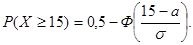
Найдем
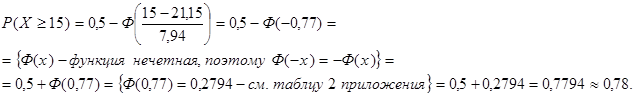 Таким образом, P(Х ³ 15)» 0,78.
Таким образом, P(Х ³ 15)» 0,78.
Это означает, что в среднем в 78 из 100рабочих дней дневная выручка оптовой базы составит не менее 15 условных денежных единиц.4
Вопросы для самопроверки.
· Генеральная и выборочная совокупности. Виды выборок. Статистическое распределение выборки.
· Что понимается под эмпирической функцией распределения, как она строится.
· Гистограмма, в чем состоит ее полезность.
· Точечные оценки. Несмещенность, состоятельность, эффективность оценок.
· Выборочная средняя, выборочная дисперсия, формулы для их нахождения.
Тема 6. Доверительный интервал. Критерий Пирсона
Литература
Забейворота В.И., Волохова К.И. Математика в экономике (Элементы математической статистики). Учебное пособие (параграф 12). УрСЭИ, Челябинск, 2001
Следует обратить внимание на суть интервального оценивания параметров распределения, на связь между доверительной вероятностью и доверительным интервалом.
Важно разобраться с тем, как находятся доверительные интервалы для оценки математического ожидания признаков, распределенных по нормальному закону.
При проверке гипотез необходимо уяснить смысл и роль таких понятий, как уровень значимости, критическая область, мощность критерия, причем в их взаимосвязи.
Безусловно, надо четко представлять общую схему статистической проверки гипотез.
Доверительным интервалом называется интервал (q*-d;q*+d), покрывающий параметр q с заданной надежностью g, где q*- точечная оценка параметра q, d-точность оценки и Р(|q* - q|<d)=g.
· Доверительный интервал для математического ожидания a нормально
распределенного количественного признака Х по выборочной средней 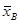
при известном s равен:
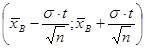 ,
,
где t находим из равенства Ф(t)= 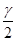 по таблице 2 приложения;
по таблице 2 приложения;
при неизвестном s равен:
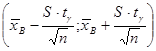 ,
,
где S= 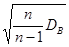 и tg находим по таблице 3 приложения tg=t(g,n).
и tg находим по таблице 3 приложения tg=t(g,n).
· Доверительный интервал для среднего квадратического отклонения s
нормально распределенного количественного признака Х по исправленному равен:
(S(1-q); S(1+q)) при q<1 и (0; S(1+q)) при q³1,
где q находим по таблице 4 приложения q=q(g,n).
· Доверительный интервал неизвестной вероятности р биноминального распределения по относительной частоте w
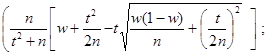
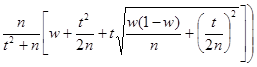 ,
,
где n–число испытаний, m–число появлений события, t находим из равенства Ф(t)= 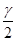 по таблице 2 приложения.
по таблице 2 приложения.
Замечание. При больших значениях n (порядка сотен) за доверительный интервал можно принять интервал равный
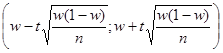 .
.
· Предельную ошибку d при нахождении доверительного интервала для математического ожидания mx и для генеральной доли р можно вычислять по одной из формул таблицы
| Выборка | ||
d=t× 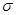
| Повторная | Бесповторная |
| для mx | 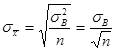
| 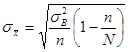
|
| для p | 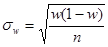
| 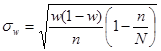
|
где t находим из равенства Ф(t)= 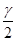 по таблице 2 приложения.
по таблице 2 приложения.
· Объем выборки n при фиксированных предельной ошибке d и доверительной вероятности g можно вычислить по одной из формул следующей таблицы
| Выборка Выборка | Повторная | Бесповторная |
| для mx | 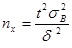
| 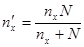
|
| для p | 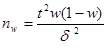
| 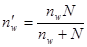
|
где t находим из равенства Ф(t)= 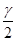 по таблице 2 приложения.
по таблице 2 приложения.
3Пример 9. В партии из 3000 изделий проверено 12 изделий. Среди них оказалось 3 бракованных изделия.
· Найти доверительную вероятность того, что доля брака во всей партии отличается от доли в выборке не более чем на 2%.
· Найти доверительный интервал, в котором с вероятностью 0,95 заключена доля брака во всей партии.
· Определить объем выборки, необходимый для того, чтобы с вероятностью 0,95 доля брака во всей партии отличалась от доли в выборке не более чем на 2%.
Date: 2015-06-05; view: 1267; Нарушение авторских прав