
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. · Найдем статистическое распределение выборки. xi 76,5 78,0 78,5 79,0 79,5 80,0 80,5 81,0 81,1 82,0 82,5
|
|
· Найдем статистическое распределение выборки.
| xi | 76,5 | 78,0 | 78,5 | 79,0 | 79,5 | 80,0 | 80,5 | 81,0 | 81,1 | 82,0 | 82,5 | 83,0 | 83,5 |
| ni |
| 84,0 | 84,5 | 85,0 | 85,5 | 86,0 | 87,0 | 89,0 | 89,5 | 91,0 |
Объем выборки 
· Размах выборки R=xmax-xmin=91,0-76,5=14,5. Так как число классов k=1+3,22×lgn=1+3,22×lg60»7, то длина частичного интервала 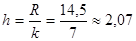
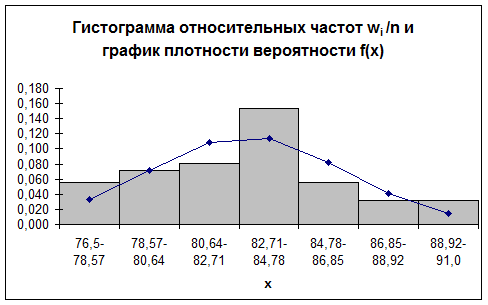
Для построения гистограммы относительных частот составим таблицу.
| Номер интервала i | Частичный интервал xi - хi+1 | Сумма частот вариант частичного интервала ni | Относительная частота
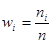
| Плотность относительной частоты 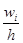
|
| 76,5-78,57 | 7/60 | 0,056 | ||
| 78,57-80,64 | 9/60 | 0,072 | ||
| 80,64-82,71 | 10/60 | 0,081 | ||
| 82,71-84,78 | 19/60 | 0,153 | ||
| 84,78-86,85 | 7/60 | 0,056 | ||
| 86,85-88,92 | 4/60 | 0,032 | ||
| 88,92-91,0 | 4/60 | 0,032 |
· Найдем несмещенную оценку математического ожидания, т.е. выборочную cреднюю 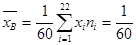 (76,5×1+78,0×2+78,5×4+79,0×3+79,5×2+80,0×1+80,5×3+81,0×2+81,1×1+82,0×3+82,5×4+83,0×7+83,5×3+84,0×4+84,5×5+85,0×3+85,5×2+86,0×2+87,0××4++89,0×2+89,5×1+91,0×1)=
(76,5×1+78,0×2+78,5×4+79,0×3+79,5×2+80,0×1+80,5×3+81,0×2+81,1×1+82,0×3+82,5×4+83,0×7+83,5×3+84,0×4+84,5×5+85,0×3+85,5×2+86,0×2+87,0××4++89,0×2+89,5×1+91,0×1)= 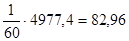 .
.
Чтобы найти несмещенные оценки дисперсии, показателей асимметрии и эксцесса, коэффициент вариации, составим таблицу.

Итак, 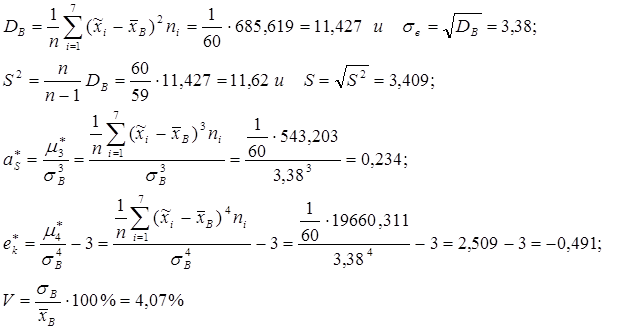
· Чтобы с помощью критерия Пирсона проверить гипотезу о нормальном распределении случайной величины Х – стоимости квартиры, нужно вычислить теоретические частоты
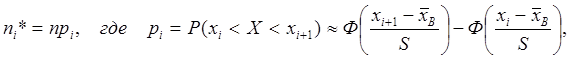 .
.
Для этого составим таблицу

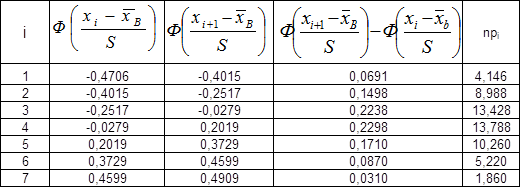
(См.таблицу 2 приложения)
Замечание. Интервалы, содержащие малочисленные эмпирические частоты (ni<5) следует объединить, а соответствующие частоты сложить.
Итак, получим таблицу
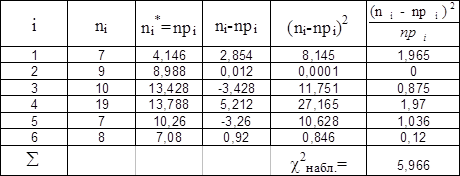
По табл. критических точек распределения c2 находим c2кр=c2(0,05;3)=7,82, т.к. уровень значимости a=0,05 по условию, а число степеней свободы k=m-s=6-3=3, потому что после объединения интервалов число интервалов равно m=6 и s=3. (См. таблицу 5 приложения)
Т.к. c2набл<c2кр, то нет оснований отклонить гипотезу о нормальном распределении генеральной совокупности.
· Чтобы построить график плотности нормального распределения c параметрами 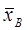 и S, заполним следующую таблицу.
и S, заполним следующую таблицу.
Для нормального распределения с параметрами 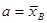 , s=S плотность вероятности
, s=S плотность вероятности  . Т.к. есть таблица значений функции
. Т.к. есть таблица значений функции 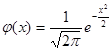 , то
, то 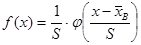 .
.
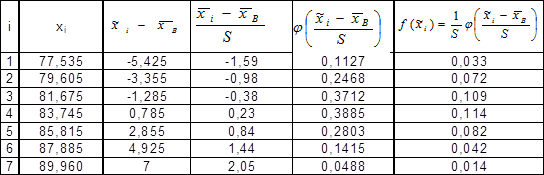
(См. таблицу 1 приложения)
Построим график плотности вероятности f(х) на том же чертеже, что и гистограмма: соединим последовательно точки (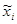 ; f(
; f( )), где i=
)), где i= 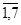 .
.
 |
Доверительный интервал для mх равен 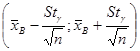 .
.
Т.к. g=0,95, то по таблице tg=t(g;n)=t(0,95;60)=2,00 (См. таблицу 3 приложения).
Итак,
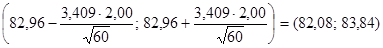 – доверительный интервал для параметра mх.
– доверительный интервал для параметра mх.
Доверительный интервал для s равен: (S(1-q); S(1+q)),
т.к. q = q(g, n)=q(0,95; 60)=0,19<1. (См. таблицу 4 приложения).
Итак, (3,409(1-0,19); 3,409(1+0,19))=(2,76; 4,05) – доверительный интервал для параметра s.4
Вопросы для самопроверки.
· Доверительный интервал и доверительная вероятность (надежность), их взаимосвязь.
· Генеральная и выборочная доли. Отклонение выборочной доли от постоянной вероятности в независимых испытаниях.
· Доверительный интервал для генеральной доли.
· Теоретические распределения, используемые при интервальном оценивании, условия их использования.
· Интервальная оценка математического ожидания нормального распределения при известном и при неизвестном среднеквадратическом отклонении этого распределения.
· Учет объема выборки при интервальном оценивании.
· Общая схема статистической проверки гипотез.
· Понятия о уровне значимости и критической области.
· Понятие о мощности критерия проверки гипотез.
· Взаимосвязь уровня значимости имощности критерия.
· Проверка гипотез о равенстве средних и дисперсии.
· Проверка гипотезы о виде закона распределения.
· Понятие о критериях согласия.
· Критерий Пирсона.
· Оценки показателей асимметрии и эксцесса, их смысл.
· Доверительные интервалы для математического ожидания и среднего квадратического отклонения.
Тема 7. Элементы теории корреляции
Литература
Забейворота В.И., Волохова К.И. Математика в экономике (Элементы математической статистики). Учебное пособие (параграф 13). УрСЭИ, Челябинск, 2001
3Пример 12. По данным наблюдений значений Х (площадь квартиры, м2) и У (цена квартиры, тыс. руб.) для однокомнатных и двухкомнатных квартир получена следующая таблица
| Х | У | Х | У | Х | У | Х | У | Х | У |
| 22,5 | 71,0 | 16,0 | 41,0 | 37,0 | 112,0 | 21,3 | 65,2 | 36,7 | 108,4 |
| 15,1 | 40,5 | 43,0 | 121,0 | 36,0 | 124,0 | 20,5 | 58,5 | 40,0 | 105,0 |
| 37,0 | 116,0 | 37,7 | 117,0 | 38,7 | 130,7 | 42,7 | 130,0 | 20,7 | 57,0 |
| 20,0 | 65,5 | 44,0 | 132,0 | 32,0 | 106,2 | 20,5 | 73,0 | 37,0 | 112,0 |
| 39,5 | 85,0 | 35,0 | 114,0 | 21,4 | 62,7 | 43,0 | 136,0 | 28,0 | 85,0 |
| 42,4 | 137,0 | 22,3 | 64,5 | 23,0 | 70,8 | 38,5 | 135,0 | 22,3 | 65,1 |
| 35,2 | 97,0 | 31,0 | 102,0 | 29,4 | 89,5 | 34,2 | 106,4 | 29,7 | 97,3 |
| 33,5 | 102,0 | 27,3 | 66,0 | 41,5 | 108,0 | 27,4 | 83,1 | 25,0 | 77,0 |
| 27,5 | 65,0 | 36,5 | 113,0 | 19,5 | 51,0 | 22,0 | 65,0 | 26,5 | 90,0 |
| 30,0 | 94,0 | 19,2 | 50,0 | 34,0 | 92,0 | 17,3 | 55,0 | 23,0 | 69,1 |
| 44,6 | 139,0 | 38,3 | 117,0 | 42,5 | 123,0 | 30,2 | 90,0 | 24,3 | 78,0 |
| 34,0 | 105,0 | 42,5 | 112,0 | 35,2 | 130,0 | 26,8 | 93,4 | 26,0 | 96,1 |
| 43,0 | 134,0 | 18,0 | 53,0 | 38,2 | 115,0 | 25,5 | 83,4 | 26,5 | 99,0 |
| 38,3 | 118,0 | 44,5 | 140,0 | 32,5 | 105,0 | 26,9 | 97,0 | 25,1 | 81,4 |
| 29,3 | 87,0 | 38,4 | 119,0 | 35,0 | 110,0 | 21,4 | 80,5 | 44,0 | 135,0 |
| 31,0 | 99,0 | 28,4 | 85,0 | 29,5 | 90,0 | 26,4 | 90,0 | 40,0 | 115,0 |
| 25,1 | 70,0 | 25,0 | 78,2 | 32,0 | 96,0 | 25,1 | 81,5 | 23,4 | 70,0 |
| 22,3 | 68,2 | 27,4 | 85,0 | 27,3 | 85,1 | 26,5 | 95,0 | 26,0 | 78,8 |
| 31,5 | 94,7 | 21,5 | 63,0 | 30,0 | 94,0 | 42,0 | 110,0 | 30,5 | 92,7 |
| 26,5 | 79,9 | 25,0 | 77,2 | 21,5 | 64,2 | 34,0 | 103,0 | 23,5 | 79,0 |
Найти выборочный коэффициент корреляции и выборочные уравнения прямых регрессии.
Date: 2015-06-05; view: 1744; Нарушение авторских прав