
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сколько различных сигналов может дать 4 семафора одновременно
|
|
a) 81
b) 9
c) 24
d) 18
7. В буфете 2 яблока и 3 груши. Каждый день в течение 5 дней подряд можно доставать по одному фрукту. Сколькими способами это может быть сделано?
a) 10
b) 24
c) 20
d) 5
8. Количество перестановок букв в слове «мера», равно...
a) 24
b) 20
c) 4
d) 12
9. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой — 6 мужчинам, по третьей — 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
a) 1680
b) 24
c) 168
d) 120
10. Сколькими способами можно поставить на шахматную доску чёрную и белую ладью так, чтобы они не били друг друга?
a) 3136
b) 1680
c) 24
d) 168
11. Укажите правильную запись высказывания: «уравнение 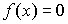 имеет хотя бы один действительный корень»
имеет хотя бы один действительный корень»
a) 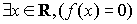
b) 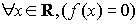
c) 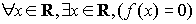
d) 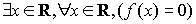
12. Количество вершин графа, изображенного на рисунке,
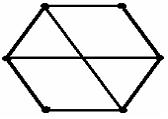
равно …
a) 6
b) 5
c) 4
d) 8
13. Матрица инциндентности графа, изображенного на рисунке,
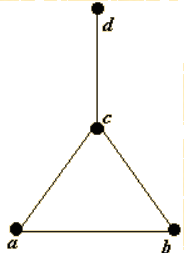
a)
| u | v | w | x | |
| a | ||||
| b | ||||
| c | ||||
| l |
b)
| u | v | w | x | |
| a | ||||
| b | ||||
| c | ||||
| l |
c)
| u | v | w | x | |
| a | ||||
| b | ||||
| c | ||||
| l |
d)
| u | v | w | x | |
| a | ||||
| b | ||||
| c | ||||
| l |
14. Матрица смежности графа, изображенного на рисунке,

a) 
b) 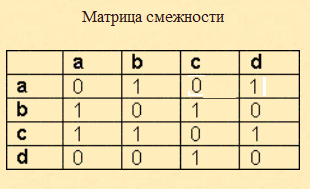
c) 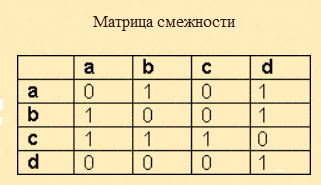
d) 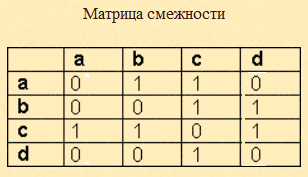
15. Количество вершин графа, изображенного на рисунке,
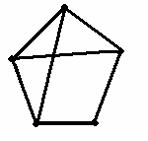
равно …
a) 5
b) 4
c) 3
d) 7
16. Какая из записей будет верной …
a) {3,7} Ì {1,3,7,9}
b) {3,7,9,11}={1,7,9,3}
c) {3,7,9} Ì {1,3,5,9}
d) {3,7} Î {1,3,5,7}
17. Пусть множества M = (8;15), N = (9,20) — представляют собой интервалы числовой оси, тогда множество K = M È N, как числовой промежуток будет равно...
a) K=(8, 20)
b) K=[8, 20]
c) K=(9, 20)
d) K=(8, 15)
18. Заданы множества А = {2,3,4,5} и D = {3,4,5}. Верным для них будет утверждение:
a) Множество D — подмножество множества A
b) Множество А — подмножество множества D
c) Множество А и множество D равны
d) Множество А — множество-степень множества D
19. Если отношение задано неравенством: 3x - 4y < 0, то данному отношению принадлежит следующая пара чисел.
a) (0;1)
b) (3;1)
c) (2;0)
d) (1;0)
20. На факультете учатся студенты, имеющие домашний персональный компьютер и студенты, не имеющие домашнего персонального компьютера. Пусть А — множество всех студентов факультета; В — множество студентов факультета, имеющих домашний персональный компьютер. Тогда разностью А\В этих множеств будет...
a) множество студентов факультета, не имеющих домашнего персонального компьютера
b) множество всех студентов факультета
c) множество студентов факультета, имеющих домашний персональный компьютер
d) пустое множество
21. Если А — множество четных натуральных чисел, а В = {11, 22, 33, 44, 55, 66, 77}, то количество элементов множества А Ç В равно...
a) 3
b) 7
c) 5
d) 4
22. Заданы множества А={1,2,3} и B={1,2,3,4,5}. Верным для них будет утверждение:
a) множество А - подмножество множества В
b) множества А и В состоят из одинаковых элементов
c) множества А и В равны
d) множество А включает в себя множество В
23. Если А — множество натуральных чисел, меньших 10, а В = {8,9,10,11,22}, то количество элементов множества А È В равно...
a) 12
b) 13
c) 10
d) 4
24. Если отношение задано неравенством: 4x - 2y > 0, то данному отношению принадлежит следующая пара чисел.
a) (1;1)
b) (-1;0)
c) (0;1)
d) (-1;1)
25. Пусть множество M = (-1;1) представляет собой интервал, а множество N = (-1;0] — отрезок числовой оси, тогда множество K = M Ç N, как числовой промежуток будет равно...
a) K=(-1,0]
b) K=[-1, 1]
c) K=(-1,0)
d) K=(-1, 1]
26. Какой является оценкой 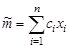 для параметра
для параметра 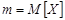 ; если
; если 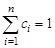 :
:
a) несмещенной
b) смещенной
c) состоятельной
d) МП-оценкой
e) несостоятельной
27. Какой является оценкой 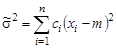 для параметра
для параметра 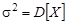 ,
, 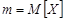 если
если 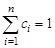 :
:
a) несмещенной
b) смещенной
c) состоятельной
d) МП-оценкой
e) Несостоятельной
28. Какой является оценкой 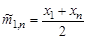 параметра
параметра 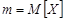 .
.
a) несмещенной; несостоятельной
b) смещенной; состоятельной
c) смещенной; несостоятельной
d) несмещенной; состоятельной
e) смещенной МП-оценкой
29. Найдите МП-оценку параметра 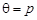 биномиального распределения генеральной совокупности
биномиального распределения генеральной совокупности 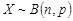 , т.е. для вероятности успеха в любом из
, т.е. для вероятности успеха в любом из 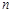 испытаний, если серии по
испытаний, если серии по 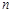 испытаний проводились
испытаний проводились 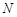 раз и в
раз и в 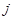 -й серии зафиксировано
-й серии зафиксировано 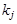 успехов,
успехов, 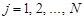 .
.
a) 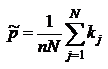
b) 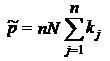
c) 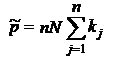
d) 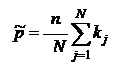
e) Нет правильного ответа
30. Найти МП-оценку параметра 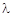 для генеральной совокупности, распределённой по показательному закону (
для генеральной совокупности, распределённой по показательному закону ( 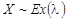 ) с функцией плотности распределения
) с функцией плотности распределения 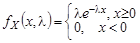 .
.
a) 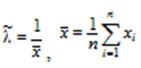
b) 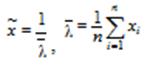
c) 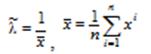
d) 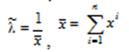
e) Нет правильного ответа
31. Найдите МП-оценку параметра 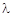 для генеральной совокупности, распределённой по закону Пуассона (
для генеральной совокупности, распределённой по закону Пуассона ( 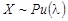 ).
).
a) 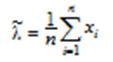
b) 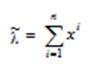
c) 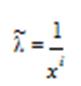
d) 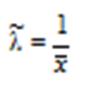
e) Нет правильного ответа
32. Найдите МП-оценку параметра 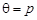 биномиального распределения генеральной совокупности
биномиального распределения генеральной совокупности 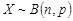 , т.е. для вероятности успеха в любом из
, т.е. для вероятности успеха в любом из 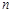 независимых повторных испытаний, если в серии из
независимых повторных испытаний, если в серии из 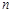 испытаний зафиксировано
испытаний зафиксировано 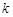 успехов.
успехов.
a) 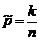 , т.е. относительная частота успеха
, т.е. относительная частота успеха
b). 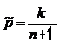 т.е. относительная частота успеха
т.е. относительная частота успеха
c) 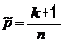 т.е. абсолютная частота успеха
т.е. абсолютная частота успеха
d) 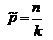 т.е. абсолютная частота успеха
т.е. абсолютная частота успеха
e) Нет правильного ответа
33. Найдите МП-оценку параметров 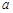 и
и 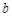 гамма-распределения,
гамма-распределения, 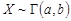 , для которого
, для которого 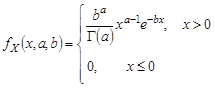 , где
, где 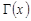 — гамма-функция, если известно, что
— гамма-функция, если известно, что 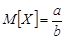 и
и 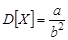
a). 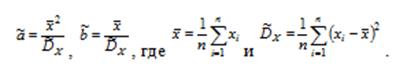
b) 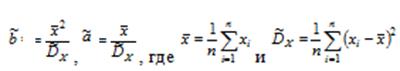
c) 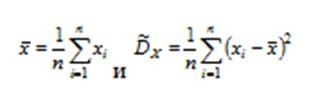
d) 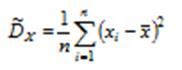
e) Нет правильного ответа
34. Монета бросается до первого выпадения герба, но не более 3 раз. Случайная величина Х — число выпадений решки, Y — число подбрасываний. Описать закон распределения случайного вектора 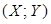 . Вычислить вероятность
. Вычислить вероятность
a) P{X<Y}=0,875
b) P{X<Y}=0,75
c) P{X<Y}=0,5
d) P{X<Y}=0,3
35. Стрелок 3 раза стреляет по мишени с вероятностью 0,7 попадания при каждом выстреле. Случайная величина Х — модуль разности между числом попаданий и числом промахов, Y — число попаданий. Описать закон распределения случайного вектора 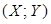 . Найти одномерные законы распределения компонент X и Y. Вычислить вероятность
. Найти одномерные законы распределения компонент X и Y. Вычислить вероятность 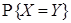 .
.
a) P{X=Y}=0,532
| Y X | 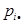
| ||||
| 0,189 | 0,441 | 0,63 | |||
| 0,027 | 0,343 | 0,37 | |||
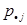
| 0,027 | 0,189 | 0,441 | 0,343 |
b) P{X=Y}=0, 5
| Y X | 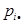
| ||||
| 0,18 | 0,4 | 0,6 | |||
| 0,02 | 0,020 | 0,020 | 0,3 | 0,37 | |
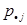
| 0,041 | 0,183 | 0,427 | 0,349 |
c) P{X=Y}=0,3
| Y X | 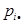
| ||||
| 0,4 | 0,6 | ||||
| 0,02 | 0,020 | 0,3 | 0,4 | ||
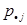
| 0,041 | 0,183 | 0,427 | 0,349 |
d) P{X=Y}=0, 15
| Y X | 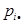
| ||||
| 0,15 | 0,4 | 0,6 | |||
| 0,02 | 0,020 | 0,020 | 0,15 | 0,37 | |
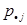
| 0,041 | 0,183 | 0,15 | 0,349 |
36. Система случайных величин 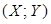 подчинена закону распределения с плотностью
подчинена закону распределения с плотностью
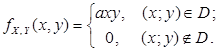
Область D – квадрат, ограниченный прямыми 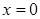 ,
, 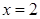 ,
, 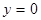 ,
, 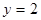 . Найти коэффициент а.
. Найти коэффициент а.
a) а=0,25
b) а=0, 5
c) а=0,15
d) а=0,2
37. Случайный вектор 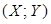 имеет плотность распределения
имеет плотность распределения
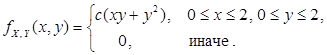
Найти: 1) постоянную c; 2) вероятность 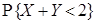 .
.
a) 3/28; 2) 3/14
b) 3/18; 2) 3/9
c) 3/8; 2) 3/4
d) 3/4; 2) 3/14
38. Случайный вектор 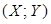 имеет функцию распределения
имеет функцию распределения
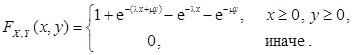
Найти законы распределения компонент X и Y.
a) X~ E (l), Y~ E (m)
b) X~ E (l2), Y~ E (m)
c) X~ E (l), Y~ E (m2)
d) X~ E (1/l), Y~ E (1/m)
39. Случайный вектор 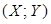 имеет функцию распределения
имеет функцию распределения
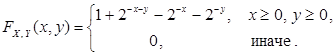
Найти: двумерную плотность распределения случайного вектора 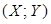 .
.
a) fX,Y(x,y)=2-x-y (ln(2), при x>=0, y>=0; 0, иначе
b) fX,Y(x,y)=2x-y (ln(2), при x>=0, y>=0; 0, иначе
c) fX,Y(x,y)=0, при x>=0, y>=0; 2-x-y (ln(2), иначе
d) fX,Y(x,y)=2-(x+y) (ln(1/2), при x>=0, y>=0; 0, иначе
Date: 2015-06-05; view: 4402; Нарушение авторских прав