
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Законы распределения основных статистик для нормальной генеральной совокупности
|
|
В некоторых вопросах представляют интерес законы распределения различных статистик, т.е. функций Z = Z (X 1, X 2,..., Xn) случайной выборки (X 1, X 2,..., Xn) из генеральной совокупности X. Например, такими статистиками могут быть выборочное среднее, выборочные дисперсии отношение выборочных дисперсий двух генеральных совокупностей и т.п.:
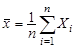 (выборочное среднее), (выборочное среднее),
| |
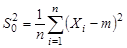 (выборочная дисперсия, m = M [ X ] известно), (выборочная дисперсия, m = M [ X ] известно),
| |
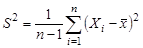 (исправленная выборочная дисперсия). (исправленная выборочная дисперсия).
|
Рассмотрим законы распределения основных статистик для одной или двух генеральных совокупностей в предположении, что генеральные совокупности имеют нормальный закон распределения.
Распределение выборочной дисперсии 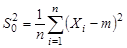
Поскольку 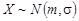 , то и
, то и 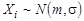 , поэтому
, поэтому
| (10.10) | 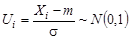 . .
|
Представим S 0 в виде 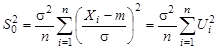 . Учитывая независимость в совокупности элементов Xi случайной выборки получаем:
. Учитывая независимость в совокупности элементов Xi случайной выборки получаем: 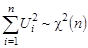 (распределение «хи-квадрат»). Таким образом,
(распределение «хи-квадрат»). Таким образом, 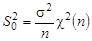 или, в стандартизованном виде
или, в стандартизованном виде
| (10.11) | 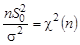
|
(напомним, что символом x 2(n) мы обозначаем не только закон распределения, но и случайную величину, описываемую этим законом).
Распределение исправленной дисперсии 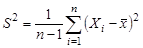
Для исправленной выборочной дисперсии можно доказать справедливость соотношения:
| (10.12) | 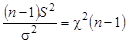 . .
|
Распределение выборочного среднего 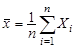 (
(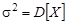 известно)
известно)
Как уже отмечалось, 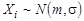 , поэтому, в силу композиционной устойчивости нормального закона распределения получаем:
, поэтому, в силу композиционной устойчивости нормального закона распределения получаем: 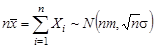 . Далее, поскольку линейное преобразование
. Далее, поскольку линейное преобразование 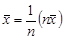 сохраняет вид закона распределения, то
сохраняет вид закона распределения, то 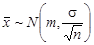 . Переходя к стандартизованному распределению N (0,1), получаем:
. Переходя к стандартизованному распределению N (0,1), получаем:
| (10.13) | 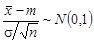 . .
|
Распределение выборочного среднего 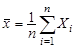 (
(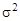 неизвестно)
неизвестно)
Если среднеквадратичное отклонение 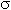 генеральной совокупности X неизвестно, то вместо этого параметра используют его точечную оценку
генеральной совокупности X неизвестно, то вместо этого параметра используют его точечную оценку 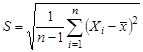 . Тогда получается соотношение
. Тогда получается соотношение
| (10.14) | 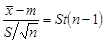
|
(напомним: символом St (k) обозначается как распределение Стьюдента, так и случайная величина с этим законом распределения).
Задача. Используя представление статистики
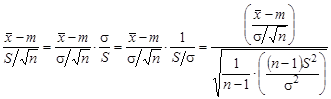
|
а также формулы (10.12), (10.13), убедитесь в справедливости соотношения (10.14).
Date: 2015-06-05; view: 788; Нарушение авторских прав