
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Распределение Фишера
|
|
Пусть x 2(k 1) и x 2(k 2) — независимые случайные величины. Распределение случайной величины
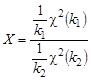
|
называют распределением Фишера с k 1 и k 2 степенями свободы. Для обозначения этого распределения используют символ F (k 1, k 2), т.е. пишут: X ~ F (k 1, k 2). Обычно и сама случайная величина X обозначается тем же символом, т.е. X = F (k 1, k 2).
Перечислим важные свойства распределения Фишера.
1. Функция плотности распределения вероятностей:
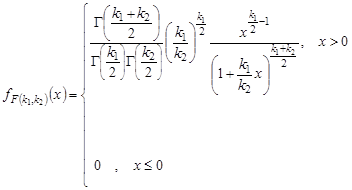
| |
| где | 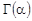 — гамма-функция. — гамма-функция.
|
2. Основные числовые характеристики:
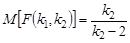 , k 2 > 2; , k 2 > 2; 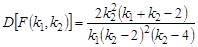 , k 2 > 4. , k 2 > 4.
|
3. Квантили Fp (k 1, k 2) распределения F (k 1, k 2) содержатся в справочниках в виде таблиц
При k 1, k 2 >> 1 для вычисления квантилей Fp (k 1, k 2) можно использовать приближённую формулу
| (10.8) | 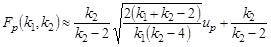
|
| где | up — квантиль порядка p распределения N (0,1). |
Важное свойство квантилей распределения Фишера состоит в том, что
| (10.9) | 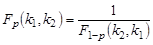 , p Î (0;1). , p Î (0;1).
|
Оно позволяет в таблицах квантилей приводить значения Fp (k 1, k 2) только для p ³ 0,5.
Пусть X ~ F (k 1, k 2). Из определения распределения Фишера следует, что в этом случае 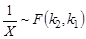 . Из того же определения видно, что X ³ 0. Поэтому для квантили Fp (k 1, k 2) порядка p Î (0;1) справедливо неравенство Fp (k 1, k 2) > 0. Отсюда следует, что при X ¹ 0 неравенства X < Fp (k 1, k 2) и
. Из того же определения видно, что X ³ 0. Поэтому для квантили Fp (k 1, k 2) порядка p Î (0;1) справедливо неравенство Fp (k 1, k 2) > 0. Отсюда следует, что при X ¹ 0 неравенства X < Fp (k 1, k 2) и  эквивалентны. С учётом сказанного, можно записать:
эквивалентны. С учётом сказанного, можно записать:
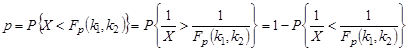 или или
| |
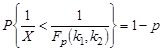 . .
|
Поскольку 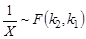 , последнее равенство означает, что число
, последнее равенство означает, что число 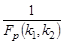 есть квантиль порядка 1 - p распределения F (k 1, k 2), т.е. что
есть квантиль порядка 1 - p распределения F (k 1, k 2), т.е. что 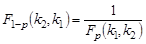 . Отсюда и следует доказываемое свойство.
. Отсюда и следует доказываемое свойство.
Date: 2015-06-05; view: 799; Нарушение авторских прав