Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пример. Закон распределения случайного вектора задан таблицей:
|
|
Закон распределения случайного вектора задан таблицей:
| X\Y | |||
| 0,1 | 0,2 | ||
| 0,3 | |||
| 0,1 | 0,3 |
Построить регрессии Y на x и X на y.
Решение. Найдем законы распределения компонент X и Y:
| X \ Y | pi | |||
| 0,1 | 0,2 | 0,3 | ||
| 0,3 | 0,3 | |||
| 0,1 | 0,3 | 0,4 | ||
| pj | 0,2 | 0,6 | 0,2 |
Построим вначале регрессию Y на x.
1) 
, 
, 
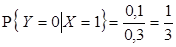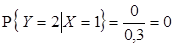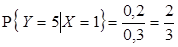, отсюда 
.
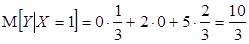2) 
, 
, 
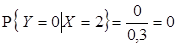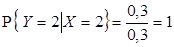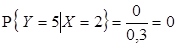, отсюда 
.
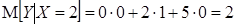3) 
, 
, 
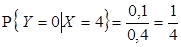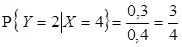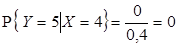, отсюда 
.
Графическое изображение регрессии Y на x показано на (рис.8.9).
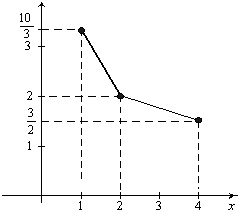
Рис. 8.9. Графики линий регрессии
Построим теперь регрессию X на y.
1) 
, 
, 
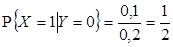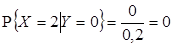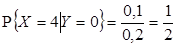, отсюда 
.
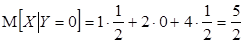2) 
, 
, 
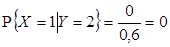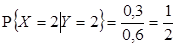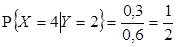, отсюда 
.
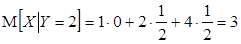3) 
, 
, 
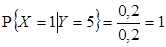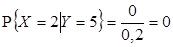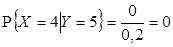, отсюда 
.
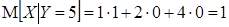Графическое изображение регрессии X на y показано на (рис. 8.10).
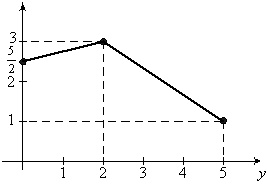
Рис. 8.10. Графическое изображение регрессии X на y
Для наглядности значения условного математического ожидания на (рис. 8.9) и (рис.8.10) соединены отрезками прямых.
Замечание 1. Для независимых случайных величин линии регрессии Y на x и X на y параллельны координатным осям, т.к. математическое ожидание каждой из них не зависит от того, какое значение приняла другая случайная величина. Линии регрессии могут быть параллельны координатным осям и для зависимых случайных величин, если только математическое ожидание каждой из них не зависит от того, какое значение приняла другая случайная величина.
Замечание 2. По аналогии с условными математическими ожиданиями можно рассматривать условные моменты. Например, условные дисперсии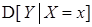 
, 
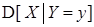и т.д.
Date: 2015-06-05; view: 656; Нарушение авторских прав