
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример. Закон распределения случайного вектора (X;Y) задан таблицей:
|
|
Закон распределения случайного вектора (X; Y) задан таблицей:
| X\Y | ||
| -1 | 0,3 | 0,25 |
| 0,1 | 0,05 | |
| 0,2 | 0,1 |
Описать условные законы распределения: 1) случайной величины X при условии Y = 1; 2) случайной величины Y при условии X = -1.
Решение. Найдем безусловные законы распределения компонент X и Y:
| X\Y | pi | ||
| -1 | 0,3 | 0,25 | 0,55 |
| 0,1 | 0,05 | 0,15 | |
| 0,2 | 0,1 | 0,3 | |
| p j | 0,6 | 0,4 |
1) Условные вероятности случайной величине X принять значения xi (i = 1, 2, 3) при условии Y = 1 вычисляются по формулам:
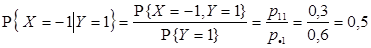
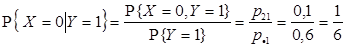
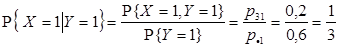
Тогда условный закон распределения случайной величины X при условии Y = 1 имеет вид:
| X | -1 | Контроль: | ||
| P{ X = xi | Y = 1} | 
| 
| 
| 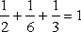
|
2) Условные вероятности случайной величине Y принять значения yj (j = 1, 2) при условии X = -1 вычисляются по формулам:
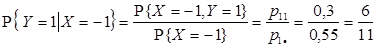
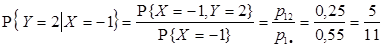
Тогда условный закон распределения случайной величины Y при условии X = -1 имеет вид:
| Y | Контроль: | ||
| P{ Y = yj | X = -1} | 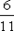
| 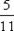
| 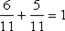
|
В общем случае условную функцию распределения случайной величины X при условии Y = y также естественно было бы определить формулой
| (8.27) | 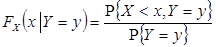
|
Однако это не всегда возможно (например, для непрерывной случайной величины Y событие { Y = y } имеет нулевую вероятность). Во избежание этих неприятностей, вместо события { Y = y } рассматривается событие { y £ Y < y + D} и D устремляется к нулю. Тогда
| (8.28) | 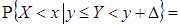 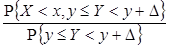 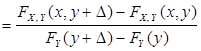
|
Тогда условной функцией распределения FX (x | Y = y) называется предел
| (8.29) | 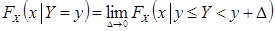
|
Оказывается, такой предел всегда существует. Аналогично
| (8.30) | 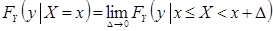
|
Если случайная величина Y непрерывна, то условную функцию распределения можно определить следующим выражением:
| (8.31) | 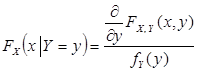
|
Аналогично
| (8.32) | 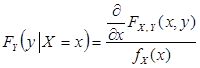
|
В наиболее важных для приложений случаях вектор (X; Y) представляет собой двумерную непрерывную случайную величину с совместной плотностью fX,Y (x,y). Тогда
| (8.33) | 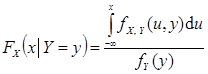 , , 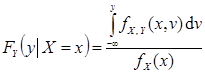 . .
|
Нетрудно видеть, что условная функция распределения FX (x | Y = y) имеет производную по x, т.е. существует условная плотность распределения случайной величины X при условии Y = y:
| (8.34) | 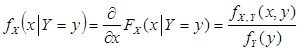
|
Аналогично
| (8.35) | 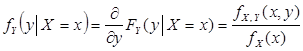
|
Date: 2015-06-05; view: 2872; Нарушение авторских прав