
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ковариация и коэффициент корреляции
|
|
Начальным моментом порядка k + s системы двух случайных величин (X; Y) называется действительное число  , определяемое по формуле:
, определяемое по формуле:
| (8.14) | 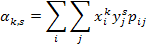
|
если (X; Y) — система двух дискретных случайных величин;
| (8.15) | 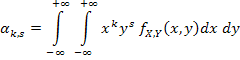
|
если (X; Y) — система двух непрерывных случайных величин.
Центральным моментом порядка k + s системы двух случайных величин (X; Y) называется действительное число  , определяемое по формуле:
, определяемое по формуле:
| (8.16) | 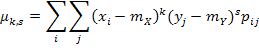
|
если (X; Y) — система двух дискретных случайных величин;
| (8.17) | 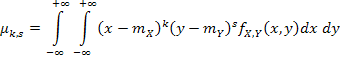
|
если (X; Y) — система двух непрерывных случайных величин.
На практике чаще всего встречаются моменты первого и второго порядков. Очевидно, что начальные моменты первого порядка есть не что иное, как математические ожидания компонент X и Y:
| (8.18) | 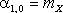 , , 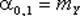 . .
|
Точка с координатами (mX; mY) на плоскости xOy представляет собой характеристику положения случайной точки (X; Y), а ее рассеивание (разброс) происходит вокруг (mX; mY).
Центральные моменты первого порядка, очевидно, равны нулю, т.е.
| (8.19) | 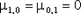
|
Имеются три начальных момента второго порядка —  ,
,  и
и  . Причем первые два из них есть не что иное, как начальные моменты второго порядка компонент X и Y:
. Причем первые два из них есть не что иное, как начальные моменты второго порядка компонент X и Y:
| (8.20) | 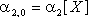 , , 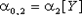 . .
|
Имеются три центральных момента второго порядка  ,
,  и
и  . Первые два из них представляют собой дисперсии компонент X и Y соответственно:
. Первые два из них представляют собой дисперсии компонент X и Y соответственно:
| (8.21) | 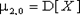 , , 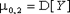 . .
|
Рассмотрим  отдельно.
отдельно.
Центральный момент второго порядка 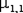 называется ковариацией случайной величины (X; Y).
называется ковариацией случайной величины (X; Y).
Для момента 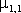 используется обозначение
используется обозначение 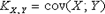 .
.
Замечание. По определению ковариации: KX,Y = KY,X.
В механической интерпретации, когда распределение вероятностей на плоскости xOy трактуется как распределение единичной массы на этой плоскости, точка (mX; mY) есть не что иное, как центр масс распределения; дисперсии D[ X ] и D[ Y ] — моменты инерции распределения относительно точки (mX; mY) в направлении осей Ox и Oy соответственно, а ковариация — это центробежный момент инерции распределения масс.
Теорема. Если случайные величины X и Y независимы, то KX,Y = 0.
Замечание. Как правило, KX,Y удобнее вычислять по формуле  .
.
Ковариация KX,Y характеризует не только степень зависимости двух случайных величин (X; Y), но также их рассеивание вокруг точки (mX; mY). Однако размерность ковариации KX,Y равна произведению размерностей случайных величин X и Y. Чтобы получить безразмерную величину, характеризующую только зависимость, а не разброс, ковариацию KX,Y делят на произведение 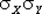 :
:
| (8.22) | 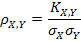
|
Величина 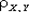 называется коэффициентом корреляции случайных величин X и Y.
называется коэффициентом корреляции случайных величин X и Y.
Коэффициент корреляции 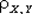 характеризует степень зависимости случайных величин X и Y, причем не любой зависимости, а только линейной, проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (или убывать). В первом случае
характеризует степень зависимости случайных величин X и Y, причем не любой зависимости, а только линейной, проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (или убывать). В первом случае 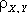 > 0 и говорят, что случайные величины X и Y связаны положительной корреляцией, во втором случае
> 0 и говорят, что случайные величины X и Y связаны положительной корреляцией, во втором случае 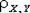 < 0 и говорят, что случайные величины X и Y связаны отрицательной корреляцией. Модуль коэффициента корреляции случайных величин X и Y характеризует степень тесноты линейной зависимости между ними. Если линейной зависимости нет, то
< 0 и говорят, что случайные величины X и Y связаны отрицательной корреляцией. Модуль коэффициента корреляции случайных величин X и Y характеризует степень тесноты линейной зависимости между ними. Если линейной зависимости нет, то 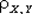 = 0.
= 0.
Теорема. Если случайные величины X и Y связывает линейная зависимость Y = aX + b, то 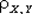 = +1 при a > 0,
= +1 при a > 0, 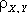 = -1 при a < 0.
= -1 при a < 0.
Пример. Найти коэффициент корреляции 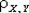 между случайными величинами: 1) X и Y = 13X - 2; 2) X и Y = 9 - 7 X.
между случайными величинами: 1) X и Y = 13X - 2; 2) X и Y = 9 - 7 X.
Решение. Согласно теореме: 1) 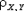 = 1, т.к. a = 13, a > 0; 2)
= 1, т.к. a = 13, a > 0; 2) 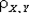 = -1, т.к. a = -7, a < 0.
= -1, т.к. a = -7, a < 0.
Ответ. 1) 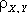 = 1; 2)
= 1; 2) 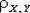 = -1.
= -1.
Пример. Игральная кость размечена таким образом, что сумма очков на противоположных гранях равна 7 (т.е. 1 и 6, 2 и 5, 3 и 4). Пусть X — число очков на верхней грани, Y — число очков на нижней грани. Построить совместный закон распределения случайных величин X и Y, найти коэффициент корреляции между ними.
Решение. По условию задачи X + Y = 7. Поэтому P{ X + Y ¹ 7} = 0. Следовательно, для построения таблицы распределения случайного вектора (X;Y) остается вычислить вероятности:
P{ X = 1, Y = 6} = P({ X = 1}{ Y = 6}) = P({ X = 1}{7 - X = 6}) = P{ X = 1} = 1/6,
P{ X = 6, Y = 1} = P({ X = 6}{ Y = 1}) = P({ X = 6}{7 - X = 1}) = P{ X = 6} = 1/6.
Аналогично можно показать, что
P{ X = 2, Y = 5} = P{ X = 5, Y = 2} = 1/6, P{ X = 3, Y = 4} = P{ X = 4, Y = 3} = 1/6.
Тогда закон распределения случайного вектора (X; Y) задается следующей таблицей:
| X\Y | ||||||
| 1/6 | ||||||
| 1/6 | ||||||
| 1/6 | ||||||
| 1/6 | ||||||
| 1/6 | ||||||
| 1/6 |
Поскольку между случайными величинами X и Y имеется линейная связь Y = 7 - X, то 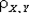 = -1.
= -1.
Ответ. 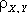 = -1.
= -1.
Теорема. Для любых случайных величин X и Y: | 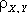 | £ 1.
| £ 1.
Определение. Случайные величины X и Y называются некоррелированными, если 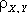 =0 (или KX,Y = 0), иначе X и Y называются коррелированными.
=0 (или KX,Y = 0), иначе X и Y называются коррелированными.
Замечание. Из независимости случайных величин следует их некоррелированность. Но из некоррелированности ( = 0) не вытекает их независимость. Действительно, если
= 0) не вытекает их независимость. Действительно, если 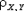 = 0, то это означает только отсутствие линейной связи между случайными величинами, однако любой другой вид связи может при этом присутствовать.
= 0, то это означает только отсутствие линейной связи между случайными величинами, однако любой другой вид связи может при этом присутствовать.
Пример. Закон распределения случайного вектора (X; Y) задан таблицей:
| X\Y | |||
| 0,1 | 0,2 | ||
| 0,3 | |||
| 0,1 | 0,3 |
Выяснить, зависимы или нет случайные величины X и Y. Найти: 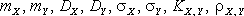 .
.
Решение. Найдем законы распределения компонент X и Y:
| X \ Y | pi | |||
| 0,1 | 0,2 | 0,3 | ||
| 0,3 | 0,3 | |||
| 0,1 | 0,3 | 0,4 | ||
| pj | 0,2 | 0,6 | 0,2 |
Очевидно, что компоненты X и Y являются зависимыми, т.к.
p 11 = 0,1 ¹ p 1 × p 1 = 0,3 × 0,2 = 0,06.
mX = 1 × 0,3 + 2 × 0,3 + 4 × 0,4 = 2,5.
mY = 0 × 0,2 + 2 × 0,6 + 5 × 0,2 = 2,2.
DX = 12 × 0,3 + 22 × 0,3 + 42 × 0,4 - 2,52 = 1,65, 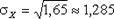 .
.
DY = 02 × 0,2 + 22 × 0,6 + 52 × 0,2 - 2,22 = 2,65, 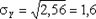 .
.
KX,Y =  1,1 -
1,1 -  1,0 ×
1,0 ×  0,1 = 1 × 0 × 0,1 + 1 × 2 × 0 + 1 × 5 × 0,2 + 2 × 0 × 0 + 2 × 2 × 0,3 + 2 × 5 × 0 + 4 × 0 × 0,1 + 4 × 2 × 0,3 + 4 × 5 × 0 - 2,5 × 2,2 = -0,9.
0,1 = 1 × 0 × 0,1 + 1 × 2 × 0 + 1 × 5 × 0,2 + 2 × 0 × 0 + 2 × 2 × 0,3 + 2 × 5 × 0 + 4 × 0 × 0,1 + 4 × 2 × 0,3 + 4 × 5 × 0 - 2,5 × 2,2 = -0,9.
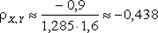 .
.
Так как 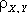 < 0, то это показывает, что между случайными величинами X и Y существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет тенденцию уменьшаться.
< 0, то это показывает, что между случайными величинами X и Y существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет тенденцию уменьшаться.
Пример. Закон распределения случайного вектора (X; Y) задан таблицей:
| X\Y | ||
| -1 | 0,15 | 0,05 |
| 0,3 | 0,05 | |
| 0,35 | 0,1 |
Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.
Решение. Найдем законы распределения компонент X и Y:
| X \ Y | pi | ||
| -1 | 0,15 | 0,05 | 0,2 |
| 0,3 | 0,05 | 0,35 | |
| 0,35 | 0,1 | 0,45 | |
| p j | 0,8 | 0,2 |
Очевидно, что компоненты X и Y являются зависимыми, т.к.
p11 = 0,15 ¹ p 1 × p 1 = 0,2 × 0,8 = 0,16.
mX = -1 × 0,2 + 0 × 0,35 + 1 × 0,45 = 0,25.
mY = 1 × 0,8 + 2 × 0,2 = 1,2.
DX = (-1)2 × 0,2 + 02 × 0,35 + 12 × 0,45 - 0,252 = 0,5875, 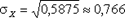 .
.
DY = 12 × 0,8 + 22 × 0,2 - 1,22 = 0,16, 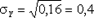 .
.
KX,Y =  1,1 -
1,1 -  1,0 ×
1,0 ×  0,1 = -1 × 1 × 0,15 + (-1) × 2 × 0,05 + 0 × 1 × 0,3 + 0 × 2 × 0,05 + 1 × 1 × 0,35 + 1 × 2 × 0,1 - 0,25 × 1,2 = 0;
0,1 = -1 × 1 × 0,15 + (-1) × 2 × 0,05 + 0 × 1 × 0,3 + 0 × 2 × 0,05 + 1 × 1 × 0,35 + 1 × 2 × 0,1 - 0,25 × 1,2 = 0; 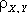 = 0.
= 0.
Этот пример показывает, что случайные величины X и Y могут быть некоррелированными, но при этом являться зависимыми.
Пример. Двумерный случайный вектор (X; Y) подчинен закону распределения с плотностью
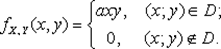
Область D — треугольник, ограниченный прямыми x + y - 1 = 0, x = 0, y = 0.
Найти: коэффициент а, 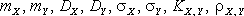 . Выяснить, зависимы или нет случайные величины X и Y.
. Выяснить, зависимы или нет случайные величины X и Y.
Решение. Коэффициент a находится из уравнения
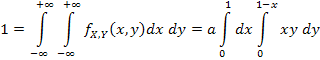
Опуская промежуточные выкладки (в этом примере будем делать так и в дальнейшем), получаем a = 24. Далее:
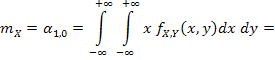

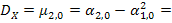
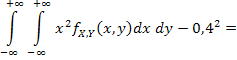
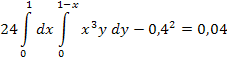
Заметим, что в силу симметрии по переменным x и y, можно не вычислять математическое ожидание и дисперсию компоненты Y, т.е. mY = mX = 0,4, DY = DX = 0,04. Тогда 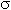 X =
X = 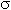 Y = 0,2.
Y = 0,2.
Вычислим ковариацию и коэффициент корреляции:
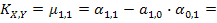
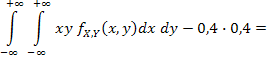
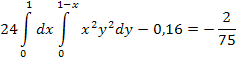 ;
; 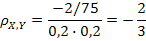
Поскольку компоненты X и Y коррелированны, следовательно, они зависимы.
Ответ. a = 24, mY = mX = 0,4, DY = DX = 0,04,  X =
X =  Y = 0,2, KX,Y = -2/75. Компоненты X и Y зависимы.
Y = 0,2, KX,Y = -2/75. Компоненты X и Y зависимы.
Пример. Двумерный случайный вектор (X; Y) равномерно распределен на множестве случайных точек Q, задаваемых неравенством | x | + | y | £ 1. Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.
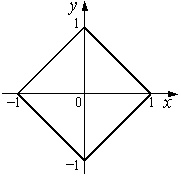
Рис. 8.6. Множество точек Q, задаваемых неравенством |x| + |y| £ 1
Решение. Множество точек Q, задаваемых неравенством |x| + |y| £ 1, является квадратом (рис. 8.6). Поскольку двумерный случайный вектор (X; Y) равномерно распределен на множестве Q, его плотность имеет вид
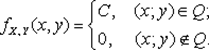
Из условия нормировки найдем константу C:
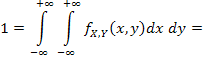
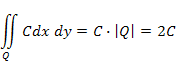
где | Q | — площадь квадрата Q, равная 2. Отсюда C = 0,5, а значит,
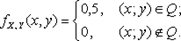
1) Найдем вначале плотность распределения компоненты X.
Если | x | > 1, то, очевидно, fX,Y (x,y) = 0 для всех y Î R.
Если | x | £ 1, то
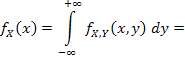
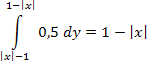 , т.е.
, т.е. 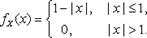 .
.
Аналогично находится плотность распределения компоненты Y:
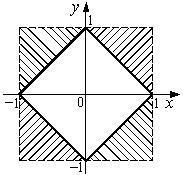
Рис. 8.7. Равенство fX,Y(x,y) = fX(x) × fY(y) не выполняется для точек координатной плоскости заштрихованных областей
Равенство fX,Y (x,y) = fX (x) × fY (y) не выполняется для точек координатной плоскости, принадлежащих заштрихованным областям (рис. 8.7), поскольку в этих точках fX,Y (x,y) = 0, а fX (x) ¹ 0 и fY (y) ¹ 0. Суммарная площадь заштрихованных областей равна 2, значит, компоненты X и Y зависимы.
2) Вычислим математические ожидания компонент X и Y:
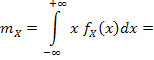
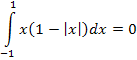
т.к. интеграл от нечетной функции в симметричных пределах равен нулю. Аналогично mY = 0.
Определим начальный момент 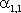 :
:
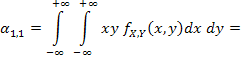
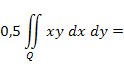
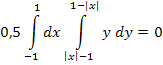
Таким образом, ковариация 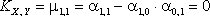 . Значит, компоненты X и Y некоррелированные.
. Значит, компоненты X и Y некоррелированные.
Ответ. компоненты X и Y зависимы, но некоррелированны.
Date: 2015-06-05; view: 4138; Нарушение авторских прав