Совместная функция распределения

Пусть на одном и том же вероятностном пространстве (W, F, P) задано n случайных величин X ₁ = X ₁(w), X ₂ = X ₂(w), …, X_n = X_n (w). Совокупность случайных величин (X ₁, X ₂,..., X_n) называется многомерной (n -мерной) случайной величиной, или (n -мерным) случайным вектором.

Пример. Широта X и долгота Y падения метеорита на Землю представляют собой двумерный случайный вектор (X; Y). В эту модель можно ввести также третью координату Z — время от начала наблюдений до момента падения первого метеорита на Землю. Тогда получится трехмерный случайный вектор (X; Y; Z).

Рассмотрим на одном и том же вероятностном пространстве (W, F, P) несколько случайных величин (X ₁, X ₂,..., X_n). Так как множества { X_k < x_k } Î F, т.е. являются событиями, то и их пересечение 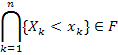. Поэтому существует вероятность этого события.

Многомерной функцией распределения 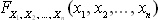называется вероятность события :

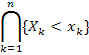(8.1)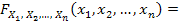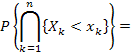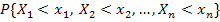

В дальнейшем изложении ограничимся случаем двух случайных величин X ₁ = X, X ₂ = Y. Поэтому будем рассматривать F_X,Y (x, y) = P{ X < x, Y < y }.

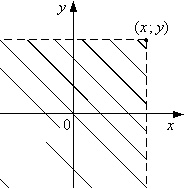
Рис. 8.1.

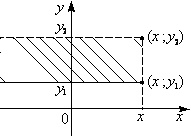
Замечание 1. Геометрически значение F_X,Y (x, y) — это вероятность попадания случайной точки (X; Y) в бесконечный квадрант с вершиной (x; y) (на рис. 8.1. этот квадрант показан штриховкой).

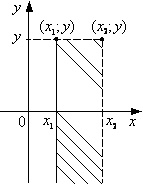
Замечание 2. С помощью F_X,Y (x, y), можно вычислять вероятности попадания случайной точки в полуполосу или в прямоугольник:

а) P{ x ₁ £ X < x ₂, Y < y } = F_X,Y (x ₂, y) - F_X,Y (x ₁, y) (рис. 8.2., а);

б) P{ X < x, y ₁ £ Y < y ₂} = F_X,Y (x, y ₂) - F_X,Y (x, y ₁) (рис. 8.2., б);

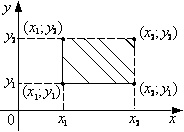
в) P{ x ₁ £ X < x ₂, y ₁ £ Y < y ₂} = (F_X,Y (x ₂, y ₂) - F_X,Y (x ₁, y ₂)) - (F_X,Y (x ₂, y ₁) - F_X,Y (x ₁, y ₁)) (рис. 8.2., в);

а)	б)	в)

Рис. 8.2. Вероятности попадания случайной точки в полуполосу или в прямоугольник

Date: 2015-06-05; view: 599; Нарушение авторских прав