Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пример. Цена деления шкалы амперметра равна 0,1А
|
|
Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.
Решение. Ошибку округления отсчета можно рассматривать как случайную величину X, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения f (x) = 1 / (b - a), где (b - a) — длина интервала, в котором заключены возможные значения X; вне этого интервала f (x) = 0. В рассматриваемой задаче длина интервала, в котором заключены возможные значения X, равна 0,1, поэтому f (x) = 1 / 0,1 = 10. Легко сообразить, что ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02, 0,08). По формуле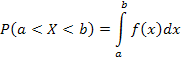 
получим.
|
Диаметр круга x измерен приближенно, причем a £ x £ b. Рассматривая диаметр как случайную величину X, распределенную равномерно в интервале (а, b), найти математическое ожидание и дисперсию площади круга.
Решение. Найдем математическое ожидание площади круга — случайной величины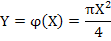 
— по формуле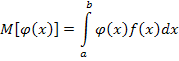 
Подставив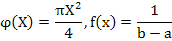 
и выполнив интегрирование, получим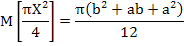 
Найдем дисперсию площади круга по формуле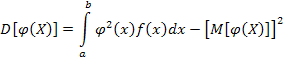 
Подставив 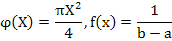и выполнив интегрирование, получим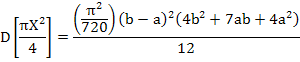 
Задача Случайные величины X и Y независимы и распределены равномерно: X — в интервале (a, b), Y — в интервале (с, d). Найти дисперсию произведения XY.
Решение.
Воспользуемся формулой D (XY) = M [(XY)2] - [ M (XY)]2 = M (X 2 Y 2) - M [(XY)]2
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, поэтому D (XY) = M (X 2) × M (Y 2) – [ M (X) × M (Y)]2 (*)
Найдем M (X 2) по формуле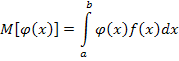
Подставляя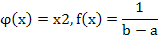 
и выполняя интегрирования получим
M (X 2) = (b 2 + ab + a 2) / 3 (**)
M (Y 2) = (c 2 + cd + d 2) / 3 (***)
Подставив M (X) = (a + b) / 2, M (Y) = (c + d) / 2, а также (**) и (***) в (*), окончательно получим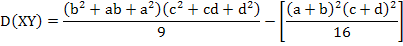 
Задача. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12, 14).
Date: 2015-06-05; view: 2395; Нарушение авторских прав