
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общая процедура принятия решений
|
|
Эффективность имитационных испытаний, в конечном счете, определяется правильностью принимаемых инженерных решений: принять образец в эксплуатацию или произвести доработку (продолжить испытания); забраковать испытанный образец или допустить его к эксплуатации и т. д. Принятию инженерного решения предшествует операция принятия статистического решения. Применение статистических методов позволяет оценить риск принятия того или иного инженерного решения, тем самым, поставив процесс принятия решения на научную основу. Содержание процесса принятия статистического решения составляет статистическая проверка гипотез – предположений о свойствах генеральной совокупности, которые могут быть проверены по данным выборки. Статистические гипотезы выдвигаются: относительно значений характеристик систем (случайных величин, и случайных функций) и относительно законов распределения параметров.
В первом случае решаются следующие основные задачи:
1) проверка соответствия полученных в ходе испытаний значений характеристик заданным в ТЗ или ТУ;
2) проверка соответствия между собой опытных значений, полученных в разных выборках.
Во втором случае:
1) проверка правомерности аппроксимации эмпирического распределения теоретическим (принадлежность выборки к известной генеральной совокупности);
2) проверка однородности распределений выборочных параметров (принадлежности двух или нескольких параметров к общей совокупности).
В дальнейшем исходную (нулевую, основную) гипотезу, выдвигаемую для проверки, будем обозначать 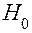 , а альтернативную (конкурирующую)
, а альтернативную (конкурирующую) 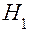 . Если гипотеза содержит только одно предположение, например
. Если гипотеза содержит только одно предположение, например 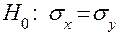 , то она называется простой. Гипотезу, состоящую из множества (конечного или бесконечного) гипотез, называют сложной, например
, то она называется простой. Гипотезу, состоящую из множества (конечного или бесконечного) гипотез, называют сложной, например 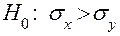 .
.
Рассмотрим последовательность решения задачи статистической проверки гипотез. На первом этапе уточняется задача исследования, после чего выбираются исходная гипотеза и одна или несколько альтернативных. Следующим этапом является выбор критерия проверки гипотез, под которым будем понимать свод правил, указывающих, при каких результатах наблюдений гипотеза 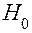 отклоняется, а при каких принимается. Выбранному критерию соответствует статистика критерия – непрерывная случайная величина с известным законом распределения, функционально связанная с результатами испытаний. Статистику критерия обозначают в соответствии с видом закона распределения (
отклоняется, а при каких принимается. Выбранному критерию соответствует статистика критерия – непрерывная случайная величина с известным законом распределения, функционально связанная с результатами испытаний. Статистику критерия обозначают в соответствии с видом закона распределения (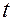 ,
, 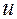 ,
, 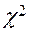 ,
, 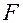 -критерий). Безотносительно к виду закона распределения статистику критерия обозначим
-критерий). Безотносительно к виду закона распределения статистику критерия обозначим 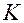 .
.
При принятии статистического решения возможны четыре случая (табл. 1), определяемые содержание гипотез 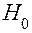 и
и 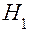 (верна, неверна) и тем, какая из гипотез окажется принятой. Вероятность опровергнуть гипотезу
(верна, неверна) и тем, какая из гипотез окажется принятой. Вероятность опровергнуть гипотезу 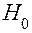 , когда она верна (совершить ошибку первого рода), называют уровнем значимости
, когда она верна (совершить ошибку первого рода), называют уровнем значимости  , а вероятность
, а вероятность 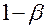 – отвергнуть
– отвергнуть 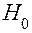 при условии ее ложности – мощностью критерия,
при условии ее ложности – мощностью критерия, 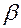 -вероятность – принять гипотезу
-вероятность – принять гипотезу 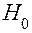 , когда справедлива гипотеза
, когда справедлива гипотеза 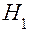 (совершить ошибку второго рода). Мощность критерия зависит от содержания
(совершить ошибку второго рода). Мощность критерия зависит от содержания 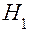 . Наиболее мощным критерием простой гипотезы
. Наиболее мощным критерием простой гипотезы 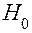 относительно простой альтернативы
относительно простой альтернативы 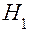 является критерий, для которого
является критерий, для которого 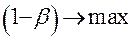 . Предпочтительно выбирать равномерно наиболее мощный критерий, который является наиболее мощным относительно любой альтернативной гипотезы.
. Предпочтительно выбирать равномерно наиболее мощный критерий, который является наиболее мощным относительно любой альтернативной гипотезы.
Таблица 1
Заключение
по гипотезе 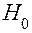
| Гипотеза 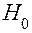
| |
| Верна | Неверна (верна 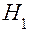 ) )
| |
| Принята | 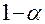 (правильное решение) (правильное решение)
| 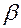 (ошибка второго рода, риск заказчика) (ошибка второго рода, риск заказчика)
|
Отвергнута (принята 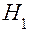 ) )
|  (ошибка первого рода, риск поставщика) (ошибка первого рода, риск поставщика)
| 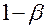 (правильное решение) (правильное решение)
|
Выбор уровня значимости  приводит к тому, что множество значений
приводит к тому, что множество значений 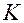 разбивается на два непересекающихся подмножества: область допустимых значений и критическую область (рис. 1). Область допустимых значений включает совокупность значений
разбивается на два непересекающихся подмножества: область допустимых значений и критическую область (рис. 1). Область допустимых значений включает совокупность значений 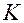 , при которых принимается гипотеза
, при которых принимается гипотеза 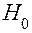 . Совокупность значений
. Совокупность значений 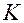 при которых
при которых 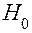 отвергается (принимается
отвергается (принимается 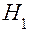 ), образует критическую область. Критическая область может быть односторонней (правосторонней, левосторонней) и двусторонней (симметричной и несимметричной). Точки, разделяющие области, называют критическими точками
), образует критическую область. Критическая область может быть односторонней (правосторонней, левосторонней) и двусторонней (симметричной и несимметричной). Точки, разделяющие области, называют критическими точками 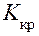 .
.
Принцип проверки статистических гипотез состоит в том, что если расчетное значение 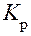 попадает в область допустимых значений, то принимают гипотезу
попадает в область допустимых значений, то принимают гипотезу 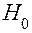 . При попадании
. При попадании 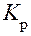 в критическую область
в критическую область 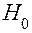 отвергается и принимается гипотеза
отвергается и принимается гипотеза 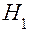 . Заметим, что принятие
. Заметим, что принятие 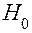 не означает, что доказана ее справедливость, а свидетельствует лишь о том, что результаты испытаний выборки не противоречат выдвинутым предположениям о свойствах объекта (генеральной совокупности). Необходимо иметь в виду, что продолжение испытаний может привести к иному заключению.
не означает, что доказана ее справедливость, а свидетельствует лишь о том, что результаты испытаний выборки не противоречат выдвинутым предположениям о свойствах объекта (генеральной совокупности). Необходимо иметь в виду, что продолжение испытаний может привести к иному заключению.
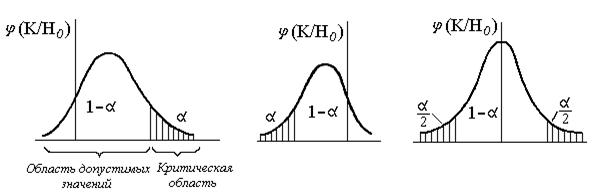
Рис. 1. Область допустимых значений и критическая область
Таким образом, правильное определение вида критической области и уровня значимости наряду с выбором статистики критерия; в основном, определяют достоверность статистического решения. В основе выбора  лежит анализ последствий совершения ошибки первого или второго рода, поскольку одновременно уменьшить
лежит анализ последствий совершения ошибки первого или второго рода, поскольку одновременно уменьшить  и
и 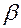 невозможно. Для случая правосторонней критической области это иллюстрируется рис. 2. Если смещать
невозможно. Для случая правосторонней критической области это иллюстрируется рис. 2. Если смещать 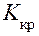 вправо [не изменяя положения кривых
вправо [не изменяя положения кривых 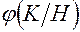 ], то с уменьшением
], то с уменьшением  мощность критерия снижается. Если
мощность критерия снижается. Если 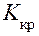 переместить влево,
переместить влево,  увеличивается, зато возрастает мощность критерия. Формализованные методы установления критической области основываются на том, что величины
увеличивается, зато возрастает мощность критерия. Формализованные методы установления критической области основываются на том, что величины  и
и 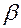 связаны с объемом испытаний
связаны с объемом испытаний  .
.
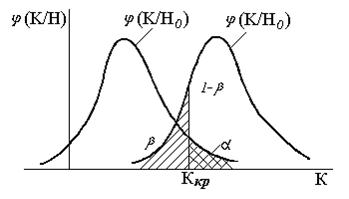
Рис. 2. Случай правосторонней критической области
Если  выбрана, то при фиксированном
выбрана, то при фиксированном  можно руководствоваться критерием Неймана-Пирсона, в соответствии с которым из всех областей фиксированного уровня
можно руководствоваться критерием Неймана-Пирсона, в соответствии с которым из всех областей фиксированного уровня  в качестве критической выбирается наиболее мощная (обеспечивающая максимум величины
в качестве критической выбирается наиболее мощная (обеспечивающая максимум величины 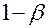 ). Увеличение
). Увеличение  (возрастание затрат на испытание) является единственным способом одновременного снижения
(возрастание затрат на испытание) является единственным способом одновременного снижения  и
и 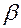 . Интуитивно значения
. Интуитивно значения  выбираются в диапазоне
выбираются в диапазоне 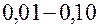 . При проверке гипотез относительно технических характеристик ракет, агрегатов наземного оборудования, артиллерийских комплексов
. При проверке гипотез относительно технических характеристик ракет, агрегатов наземного оборудования, артиллерийских комплексов 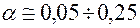 . Оценивая показатели качества (надежности, эффективности), область допустимых значений целесообразно расширить (
. Оценивая показатели качества (надежности, эффективности), область допустимых значений целесообразно расширить (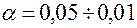 ). Более жесткие условия могут задаваться при проверке однородности характеристик контрольно-испытательной аппаратуры и свойств элементов, испытываемых в лабораторных условиях
). Более жесткие условия могут задаваться при проверке однородности характеристик контрольно-испытательной аппаратуры и свойств элементов, испытываемых в лабораторных условиях 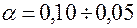 .
.
Date: 2015-05-23; view: 597; Нарушение авторских прав