Общая схема испытаний

При планировании испытаний (в узком смысле) принципиально возможны два подхода: пассивный и активный. Пассивные испытания заключаются в наблюдении и регистра­ции входных и выходных параметров объектов в режиме нормаль­ного функционирования (при фиксированных нагрузках). Плани­рование испытаний сводится к выбору стационарного режима испытаний. Активные испытания проводятся посредством наблюдения и регистрации процесса после внесения в него возмущений. Сущ­ность активного подхода заключается в одновременном варьиро­вании по определенному закону значений из совокупности факторов 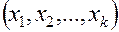, которое ведется по целесообразно составлен­ной программе, называемой матрицей планирования.

План испытания характеризуется спектром плана (нормиро­ванным спектром)

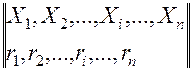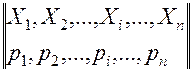или , (1)

где определяет уровни, на которых на­ходится каждый из факторов в 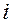-м испытании; 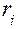– число повторных испытаний;

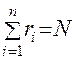, – суммарное количество испытаний, , .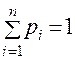

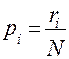Схему планирования испытаний рассмотрим применительно к случаю доводочных испытаний, проводимых с целью достижения экстремального (заданного) значения выходного параметра. Пла­нирование включает: определение пространства факторов, выбор стратегии испытаний.

Совокупность факторов 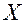должна быть достаточно полной (включать все существенные факторы), а каждый из факторов отвечать требованиям однозначности, управляемости, независи­мости и совместимости с другими факторами. Так, при опытной отработке двигателя внутреннего сгорания, когда при выбранном типе двигательной уста­новки и виде топлива решается задача обеспечения требуемой тяги 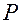и ресурса 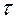, в качестве 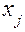могут использовать­ся тип форсунок, их количество, соотношение, размещение, тип головки, литраж и геометрия блока цилиндров, способ охлаждения и т. д.

При выборе стратегии испытаний в общем случае можно вы­делить три основных этапа.

1. Планирование и проведение испытаний в ограниченной об­ласти с конечной целью установить градиентное направление (на­правление, в котором угол наклона функции отклика максимален). Решение задачи может осуществляться с помощью линейных уравнений регрессии.

2. Последовательное движение в градиентном направлении (в частном случае «крутое восхождение»). На этом этапе, зная градиентное направление, выбирают другую ограниченную область в факторном пространстве, где и проводят новую серию испытаний. Крутое восхождение ведется до тех пор, пока не будет достигнута так называемая «почти стационарная область», в которой вариации факторов слабо влияют на значение выходных параметров.

3. Планирование и проведение испытаний в почти стационарной области, где окончательно определяется совокупность значений факторов 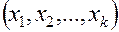, при которых обеспечивается экстремальное (требуемое) значение 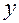. На этом этапе учитывается нелинейный характер связей между 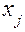и .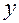

Основу современного подхода к планированию многофакторных испытаний составляют активные методы, из числа которых широкое распространение получили полные и дробные факторные планы (ПФП и ДФП). Пассивные методы сохраняют свое значе­ние в ходе проведения промышленных экспериментов на стадии серийного производства вооружения, при изучении опыта эксплуа­тации ракетных и артиллерийских комплексов в войсках, а так­же в тех случаях, когда при испытании не удается устранить шу­мовое поле, вызываемое неуправляемыми переменными или слу­чайными помехами, накладываемыми на управляемые факторы.

Полные факторные планы испытаний

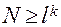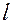Планирование по схеме полного факторного плана предусмат­ривает реализацию всех возможных комбинаций на каждом из вы­бранных уровней. Общее количество испытаний , где – количество уровней, 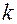– число факторов. 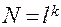, если при каждом сочетании факторов проводится только одно испытание. Если ис­пытания проводятся при двух уровнях факторов 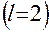, то реали­зуется план 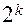, при 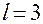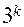и т. д. Формирование ПФП включает два этапа.

На первом этапе выбирается совокупность факторов 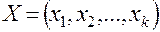, удовлетворяющих сформулированным требова­ниям, после чего определяется локальная область факторного про­странства, в которой намечается проведение испытаний. При пла­нировании по схеме 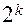эта область устанавливается посредством задания основного уровня и интервала варьирования. Основным уровнем (центром плана) называют многомерную точку 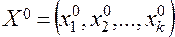в факторном пространстве. В зависимости от целей испытаний координаты могут соответствовать номиналь­ным значениям параметров или выбираться в центре области их изменения, подлежащей изучению. Интервал варьирования устанавливают симметрично относительно основного уровня и опреде­ляют для каждого из факторов по формуле

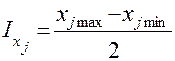, (2)

где 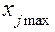, 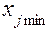– максимальные и минимальные значения каждо­го из факторов (определяющих фактор параметров).

Интервал варьирования выбирается из прогнозируемых значе­ний выходного параметра и условий технической осуществимости вариаций входных воздействий с учетом затрат на выполнение работ.

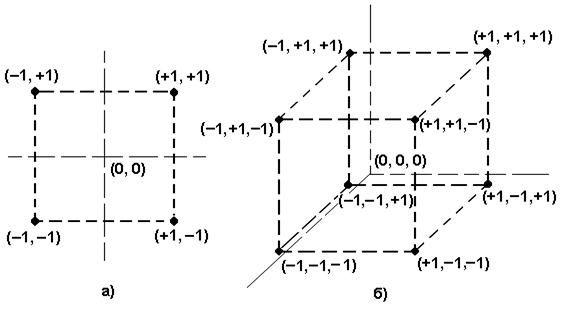
Рис. 1. Схемы ПФП типа 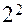и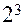

ПФП составляют в виде матрицы планирования, используя ко­дированную (безразмерную) систему координат. Переход к безраз­мерной системе координат осуществляется по формулам

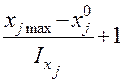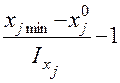; . (3)

В кодированной системе верхний уровень изменения любого фактора равен , нижний 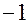, а координаты центра плана равны нулю и совпадают с началом координат. На рис. 3.1 изображены схемы ПФП типа 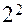и 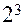– соответственно прямоугольник и куб. Матрица ПФП 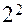, 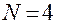приведена в табл. 1, а (обозначение 1 в таблице опущено), где столбцы (вектор-столбцы) показывают, какие значения принимает каждый из факторов 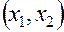в очередном испытании, а строки (вектор-строки) характеризуют режим каждого отдельного испытания. Так, например, при изуче­нии влияния условий подачи компонентов топлива на выходные параметры ЖРД первый опыт проводится при минимальных рас­ходах горючего и окислителя, четвертый – при максимальных, второй – при максимальной подаче горючего 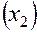и минимальной окислителя 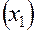и т. д.

Таблица 1

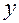
Номер опыта					Номер опыта
	+	–	–			+	–	–	+
	+	–	+			+	–	+	–
	+	+	–			+	+	–	–
	+	+	+			+	+	+	+

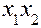
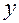
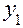
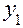
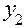
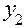
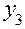
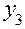
Первый столбец используется только для выполнения расче­тов ( – фиктивная переменная). В последнем столбце записы­ваются результаты испытания.

Порядок перехода от плана 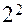к плану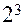 показан в табл. 2. Аналогично методом «перевала» можно перейти к пла­нам с большим числом факторов.

Таблица 2

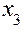
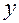
Номер опыта						Номер опыта
	+	–	–	–			+	–	–	+
	+	–	+	–			+	–	+	+
	+	+	–	–			+	+	–	+
	+	+	+	–			+	+	+	+

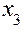
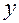
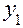
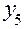
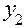
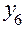
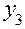
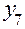
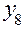
Приведенные в табл. 1 и 2 матрицы планирования обладают свойствами ортогональности, симметричности и нормировки.

Свойство симметричности относительно центра опыта заключается в том, что алгебраическая сумма элементов вектор-столбцов каждого из факторов равна нулю:

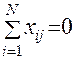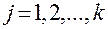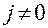; ; . (4)

Условие нормировки подтверждается равенством сум­мы квадратов элементов каждого столбца числу опытов:

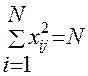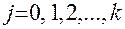; . (5)

Свойство ортогональности определяется равенством нулю произведений любых двух вектор-столбцов:

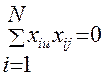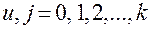; . (6)

Предполагается, что при перемножении элементов с одноимен­ными знаками получаем , с разноименными .

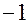Свойство ортогональности позволяет резко уменьшить трудо­емкость вычислений коэффициентов регрессии, так как матрица нормальных уравнений становится диагональной, причем ее диагональные элементы равны числу испытаний , заданных мат­рицей ПФП.

Воспользуемся матрицей планирования (табл.1) для по­лучения уравнения регрессии вида

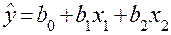. (7)

При вычислении 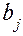оценок коэффициентов регрессии 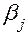по формуле последовательно получим

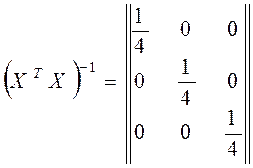
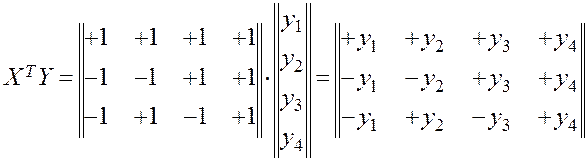
Отсюда

; ;

; .

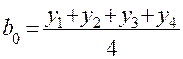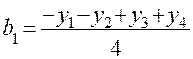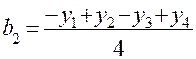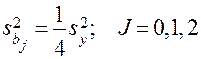Таким образом, каждый из коэффициентов 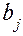вычисляется не­зависимо и по простой формуле, которая в общем случае имеет вид

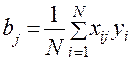. (8)

Поскольку все диагональные элементы матрицы ошибок 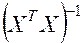равны между собой, каждая из оценок 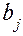получена с одинаковой (и минимальной) дисперсией

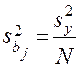, (9)

где 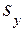– ошибка опыта.

Рассмотренные ПФП являются оптимальными в том смысле, что при их реализации для данного числа испытаний определи­тель матрицы ошибок 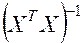минимален. Геометрически это означает, что сведен к минимуму объем эллипсоида рассеивания оценок параметров. Важным свойством полученных планов яв­ляется также рототабельность, которая заключается в том, что точность предсказания значений выходной характеристи­ки 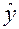одинакова на равных расстояниях от центра плана и не зависит от направления.

План типа 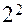позволяет получить модель в виде уравнения вто­рого порядка

.

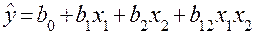Для вычисления коэффициента 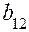, характеризующего совмест­ное воздействие факторов и вводится дополнительный век­тор-столбец 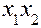(табл.1), элементы которого определяют, пе­ремножая попарно элементы столбцов и .

Расширенная матрица ПФП 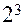, обеспечивающая получение мо­дели в виде более сложного полинома

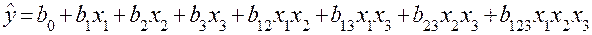
представлена в табл. 3. В нижней строке таблицы приведены вы­численные по формуле (8) оценки коэффициентов 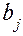. Значе­ния 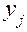содержатся в последнем столбце.

Например,

;

.

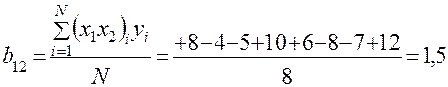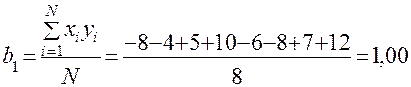Таблица 3

Номер опыта
	+	–	–	–	+	+	+	–
	+	–	+	–	–	+	–	+
	+	+	–	–	–	–	+	+
	+	+	+	–	+	–	–	–
	+	–	–	+	+	+	–	+
	+	–	+	+	–	–	+	–
	+	+	–	+	–	–	–	–
	+	+	+	+	+	+	+	+
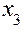
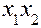
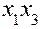
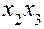
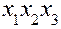
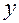
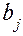
	7,5			0,625	1,5	–2	0,75	-0,75

Дробные факторные планы испытаний. Планирование испытаний

Можно сократить число испытаний, если от ПФП перейти к дробным факторным планам, или дробным репликам от полного факторного эксперимента. При переходе от ПФП к ДФП важно сохранить ортогональность матрицы планирования. С этой целью в качестве реплики (ДФП) пользуются ПФП для меньшего числа факторов. Такая возможность существует, поскольку в ПФП число испытаний значительно превосходит количество определяемых ко­эффициентов линейной модели.

Пусть требуется получить уравнение регрессии вида

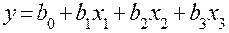. (10)

Для решения задачи можно ограничиться четырьмя испытания­ми 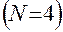, если в ПФП 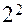(табл. 4, а) столбец 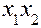использовать в качестве плана для 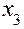(табл. 4, а). Теперь элементы столбца 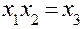служат не для расчета оценки 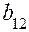, а характеризуют уро­вень фактора 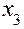в каждом из опытов. Использованный план составляет половину ПФП 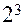, называется полурепликой ( 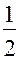-репли­кой) от 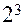и записывается формулой 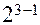. В рассмотренной задаче возможны два варианта ДФП (табл. 4, а, б).

Таблица 4

а) б)

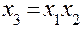
Номер опыта					Номер опыта
	–	–	+			–	–	–
	–	+	–			–	+	+
	+	–	–			+	–	+
	+	–	+			+	+	–

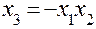
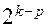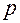Общее правило перехода от ПФП к ДФП сводится к следую­щему: для сокращения числа испытаний новому фактору присваи­вается вектор-столбец, принадлежащий взаимодействию, которым можно пренебречь. Формула ДФП имеет вид , где – количе­ство факторов, введенных посредством замещения исключаемых из рассмотрения взаимодействий. В зависимости от соотношения чисел 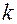и 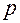реализуются 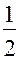, , 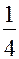и т. д. реплики ПФП.

Сокращение числа испытаний в рассмотренном примере достиг­нуто за счет утраты части информации: из рассмотрения исключе­но парное взаимодействие 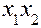. В результате полученные оценки 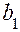, , 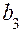оказались смешанными оценками генеральных коэффи­циентов

; ; ,

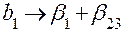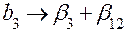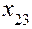поскольку соответствующие вектор-столбцы совпадают ( неразличимо с и т. д.). Эффективность ДФП определится тем, насколько удачно выбрана система смешивания линейных эффек­тов и эффектов взаимодействий. Поэтому при обращении к ДФП необходимо уметь заранее установить, какие из 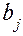, 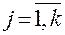явля­ются несмешанными оценками соответствующих генеральных коэффициентов – определить разрешающую способность дробных реплик. Для этого находят применение понятия генерирующего со­отношения и определяющего контраста.

Соотношение, показывающее, с каким из эффектов смешан рассматриваемый эффект, называют генерирующим. В рассмотрен­ном примере это 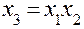или 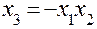. Определяющим контрас­том называется символическое обозначение произведения столб­цов. Умножая левую и правую части определяющего контраста на 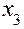и памятуя, что 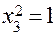, получим определяющий контраст 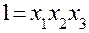или 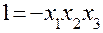. Теперь, последовательно умножая левые и правые части на , , , 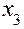можно выявить систему смешивания фак­торов. Для ДФП (табл. 4,б)

; ; ,

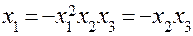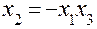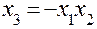откуда следует система смешивания

; ; .

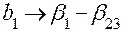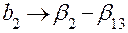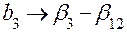Для ДФП (табл. 2.5, а) аналогичным путем получаются приведен­ные ранее соотношения.

Обращаясь к ДФП 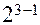, заметим, что матрица (табл. 4, а, б) совпадает с ПФП 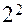(табл. 1). Иначе план 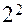является опор­ным при построении дробной реплик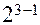и . При 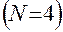с помощью ДФП удается учесть только один дополнительный фактор. Оце­ним, сколько же дополнительных факторов можно учесть, исполь­зуя в качестве опорного ПФП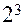 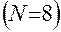. Из табл. 3 видно, что можно частично или полностью замещать четыре взаимодей­ствия 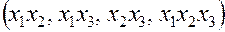то есть вводить дополнительно до четы­рех факторов. При замещении одного фактора имеет место ДФП 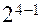( 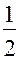-реплика от ПФП 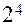), двух – 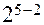( 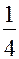от ПФП 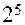),трех – 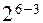( от 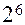), четырех – 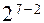( 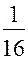от ПФП 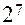). Если замещению подлежат все взаимодействия, то план называют насыщенным. В этом случае в модели учитываются только линейные взаимодейст­вия. Для всех рассмотренных ДФП 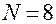. Сравним, что при реализа­ции ПФП, если 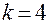, то 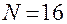(используется ПФП 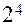); при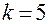 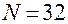(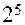); при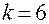 (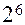); при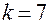 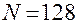(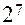). В табл. 5 приведен пример формирования ДФП 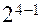при различном выборе генерирующих соотношений.

Последовательность формирования ДФП включает: уяснение количества факторов и допустимого числа (в примере 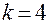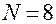), выбор реплики (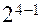), построение опорного плана (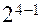), уста­новление генерирующих соотношений, нахождение определяющего контраста (обобщенного контраста), уяснение системы смешива­ния.

Выбор системы смешивания осуществляется на основе анализа физической сущности процесса, изучения конструкторской документации и данных предшествующих этапов испытаний. В общем случае стремятся отсеивать взаимодействия относительно высоких порядков.

Таблица 5

Генерирующее соотношение
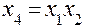
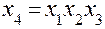
Определяющий контраст
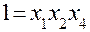
Система смешивания
,	,
,	,
,	,
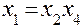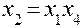
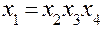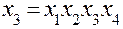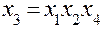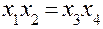
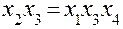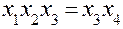
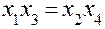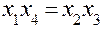
Система оценок
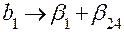
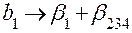
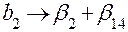
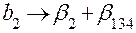
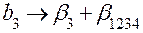
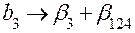
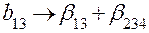
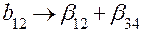
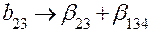
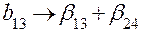
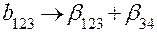
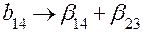
Вид модели

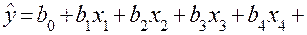
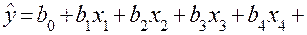
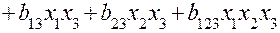
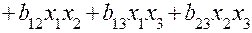
При выборе, например, ДФП 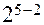( 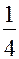-реплики) возможны 12 вариантов решения. Если принять 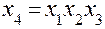, , 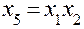то система смешивания задается обобщающим определяющим контрастом, который получают, перемножая определяющие контрасты 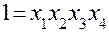и 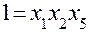между собой:

.

Тогда получается следующая система совместных оценок:

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; .

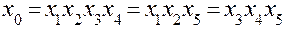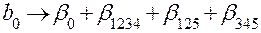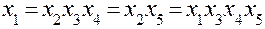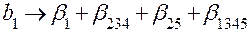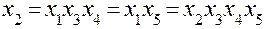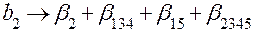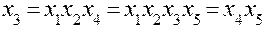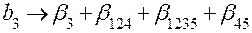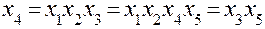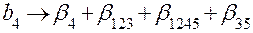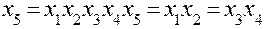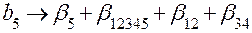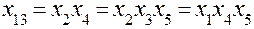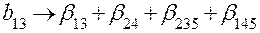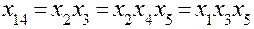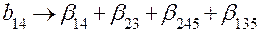Соответствующий план испытаний показан в табл. 6.

Таблица 6

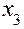
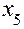
Номер опыта						Номер опыта
	–	–	–	–	+		–	–	+	+	+
	–	+	–	+	–		–	+	+	–	–
	+	–	–	+	–		+	–	+	–	–
	+	+	–	–	+		+	+	+	+	+

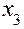
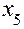
ДФП типа 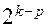, как и ПФП, обладают следующими преимуще­ствами: они ортогональны; каждый из коэффициентов вычисляет­ся по всем испытаниям; все коэффициенты вычисляются с оди­наковой и минимальной дисперсией.

При проведении испытаний учитывают, что изменение выход­ного параметра 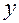из-за влияния неконтролируемых факторов име­ет случайный характер. Поэтому предусматривается случайный порядок проведения испытаний (рандомизация факторов). С этой целью последовательность испытаний (реализация строк матрицы планирования) определяется с помощью таблицы случайных чисел.

Date: 2015-05-23; view: 877; Нарушение авторских прав