Экспоненциального сглаживания

Для прогнозирования характеристик образцов техники, мате­матическое описание которых имеет вид

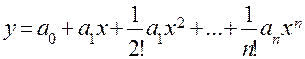, (4.10)

целесообразно применять метод экспоненциального сглаживания. Сложившаяся практика использования этого метода пред­полагает ограничение числа членов ряда Тейлора

,

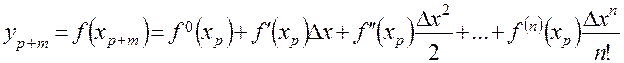(4.11)

аппроксимирующего выражение (4.10), несколькими членами .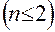

В зависимости (4.11) 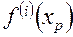– 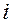-я производная функции по переменной в точке 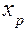; ; 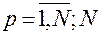– число наблюдений; 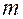– значение величины шага упреждения.

Для условий, когда ошибки прогнозирования не удовлетворя­ют заданным требованиям, можно осуществить анализ их источников. Известно [4], что точность прогнозной задачи можно опреде­лить по зависимости

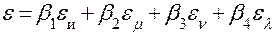, (4.12)

где ;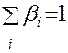

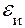– погрешность, обусловленная приближенностью исход­ной информации;

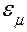– погрешность, связанная с методом прогнозирования;

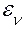– погрешность, вызванная неточностью вычислений;

– нерегулярная погрешность, обусловленная вероятно­стью непредсказуемых в настоящее время событий, влияющих на характер изменения прогнозируемой ве­личины.

Одной из наиболее весомых является методическая ошибка, за­висящая от числа членов разложения. В работах [1], [2] приво­дятся аналитические зависимости для выполнения параметров ап­проксимирующего многочлена при . Вывод таких зависимо­стей для 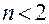представляет значительные трудности. Кроме того, любое увеличение числа членов выражения (4.11) влечет за собой потребность увеличения объема исходных данных, необходимых для определения оценок начальных значений коэффициентов 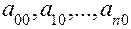(методом наименьших квадратов или в более об­щем случае методом максимального правдоподобия), далее пред­лагается модификация метода экспоненциального сглаживания, основанная на принципах группового учета аргументов. Сущность метода заключается в том, что математическая модель объекта прогнозирования

,

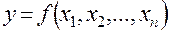называемая в соответствии с терминологией работы [1] его «пол­ным описанием», заменяется набором «частных описаний» вида

.

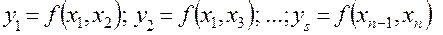По принятому критерию, значение которого вычисляется для каждого «частного описания», из множества 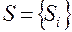отбирается некоторое число, называемое «свободой выбора», наиболее регу­лярных описаний, образующих подмножество 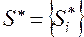. Вычис­ленные значения промежуточных аргументов 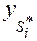принимаются в качестве аргументов «частных описаний» следующего уровня фильтрации, то есть

.

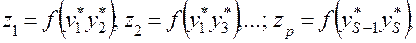Аналогичная процедура повторяется до тех пор, пока величина критерия фильтрации уменьшается или увеличивается в зависи­мости от его содержания (при этом исходная информация делится на две выборки: обучающую и проверочную). Для практических расчетов в качестве такого критерия рекомендуется принимать среднеквадратическую ошибку аппроксимации модели на проверочной выборке, которая, как установлено в работе [10], при увеличении числа уровней фильтрации, а, следовательно, сложности модели, достигает экстремального значения. Сложность модели (измеряется числом ее членов), соответствующая экстремальному значению критерия, является оптимальной. На последнем уровне фильтрации фиксируется «частное описание», значение которого минимально. На предпоследнем уровне выбираются «частные описания», являющиеся аргументами последнего уровня, и т.д. Так как «частные описания» являются функцией двух аргументов, их коэффициенты легко определяются по небольшому количеству исходных данных. Исключая промежуточные переменные 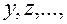можно получить модель исследуемых характеристик объекта прогнозирования в виде аналога «полного описания»

,

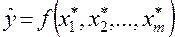где в общем случае .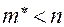

Как известно, особые трудности при увеличении числа членов в разложении Тейлора связаны с получением аналитических зави­симостей для определения вектора коэффициентов 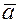. Из рабо­ты [2] следует, что

,

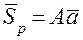где – вектор-столбец размером 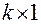сглаженных значений процесса

;

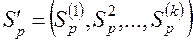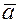– вектор-столбец размером 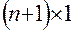неизвестных коэф­фициентов

;

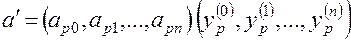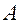– матрица размером 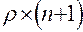, элементы которой, соот­ветствующие 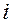-й строке и 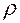-му столбцу, вычисляются по зависимости

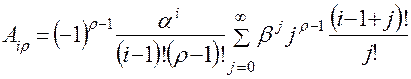. (4.13)

В связи с тем, что сглаженные значения процесса могут быть определены по зависимости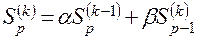

вектор 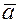выражается зависимостью 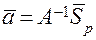. (4.14)

Анализ зависимости (4.13) показывает, что наибольшую слож­ность вызывает вычисление суммы бесконечного ряда, представ­ляющего собой произведение степеней показательной функции и отношения факториалов, которое можно упростить путем неслож­ных преобразований:

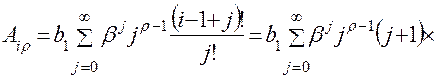
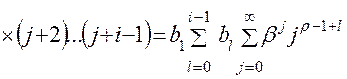, (4.15)

где ;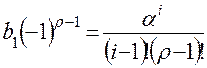

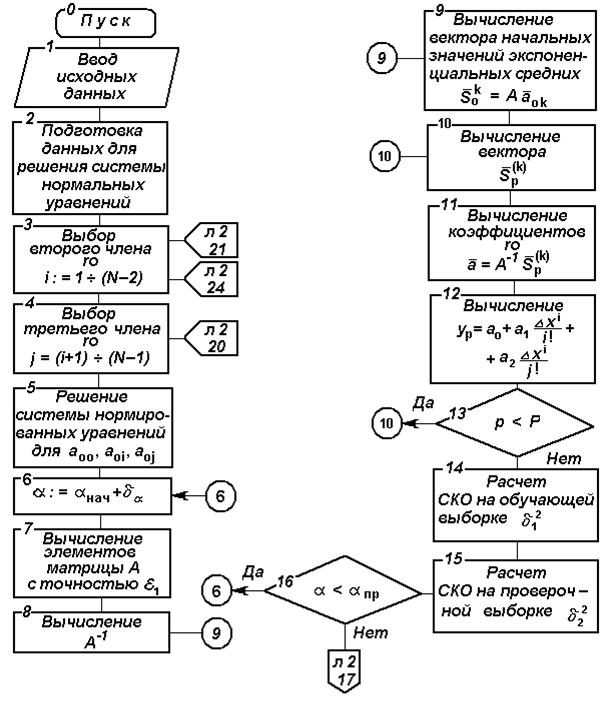
Рис. 4.4. Блок-схема алгоритма прогнозирования по методу модифици­рованного

экспоненциального сглаживания

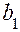– коэффициенты многочлена с переменной .

С учетом, что при 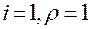ряд (4.15) вырождается в беско­нечно убывающую геометрическую прогрессию со знаменателем 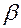, сумма которой равна 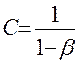, сумма любого ряда вида (4.15) может быть вычислена

по рекур­рентной зависимости

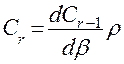, (4.16)

где .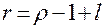

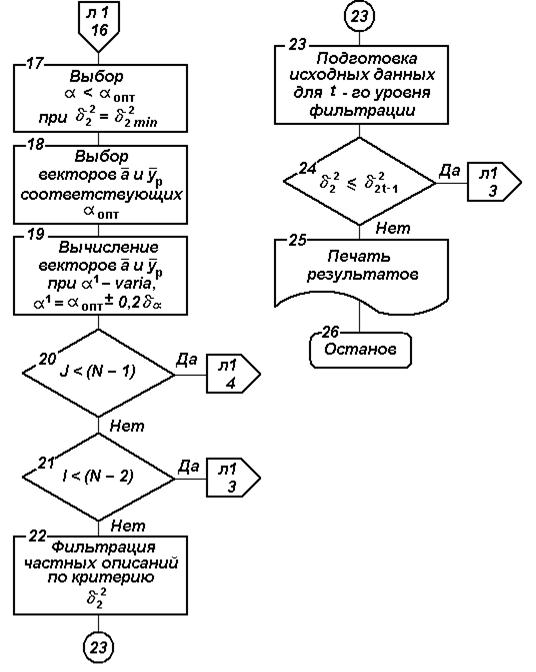
Рис. 4.4. Блок-схема алгоритма прогнозирования по методу

модифици­рованного экспоненциального сглаживания (продолжение)

Расчеты по формуле (4.16) при машинной реализации алго­ритма можно осуществлять только численным дифференцирова­нием, использование которого нецелесообразно. Поэтому вычисле­ние элементов матрицы 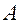рекомендуется выполнять на ЭВМ по зависимости (4.13) с заданной точностью при ограниченном зна­чении 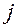. Получив, таким образом, элементы матрицы 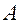и вычислив обратную матрицу 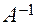, вектор коэффициентов 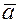определяется по формуле (4.14). Далее, не нарушая общности рассуждений, заме­тим, что в качестве частных описаний целесообразно использовать зависимость вида

.

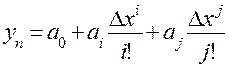Блок-схема алгоритма прогнозирования, составленного в соот­ветствии с изложенными положениями, изображена на рис.4.4.

Date: 2015-05-23; view: 778; Нарушение авторских прав