Автоматический подбор вида экстраполируемой функции

Методы экстраполяции в прогнозировании основаны на выяв­лении основной тенденции и проведении на ее базе необходимых расчетов. Поэтому выбор правильной формы связи между факто­ром-функцией и фактором-аргументом является важным этапом. Для прогнозирования применяются различные формы связи: ли­нейная, параболическая, степенная, показательная и др. Но эти формы имеют жесткую, раз и навсегда заданную структуру. В свя­зи с этим при прогнозировании во многих случаях целесообразно использовать так называемые функции с гибкой структурой (ФГС), форма которой может изменяться и автоматически приспосабли­ваться к изучаемому процессу. Функция с гибкой структурой ха­рактеризует не только зависимость одного фактора от другого, но и собственно тенденцию развития каждого фактора. Заманчивая идея метода автоматического получения вида и параметров ап­проксимирующей функции принадлежит Н. К. Куликову. Однако на пути практической реализации метода имеется немало трудно­стей, например при решении систем трансцендентных уравнений, которые возникают в процессе поиска параметров ФГС или при вычислении соответствующих производных в случае табличного способа задания функции. Очевидно, по мере преодоления труд­ностей практической реализации функции с гибкой структурой будут занимать все более заметное место в арсенале экстраполяционных методов прогностики. Особую роль в развитии метода следует отвести ЭВМ, что способствует разработке новых эффек­тивных алгоритмов, пригодных для решения задач прогнозирова­ния на основе ФГС. Два частных случая использования ФГС рас­сматриваются далее.

Известно [1], [2], [3], что любой процесс можно представить в

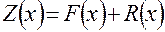, (4.17)

где 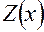– исходный процесс (функция одного переменного);

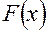– приближенная модель процесса (описание с помощью ФГС);

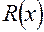– остаток (некоторая функция точности приближения).

В наиболее общем виде ФГС для одного аргумента записывает­ся в виде [1], [2]

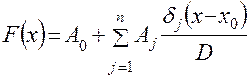, (4.18)

где 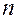– некоторое фиксированное натуральное число;

– начальное значение фактора-аргумента на рассматриваемом интервале;

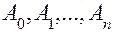– постоянные действительные параметры;

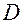– специальный (степенной) определитель 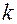-го порядка;

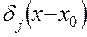– функция, получаемая из определителя заме­ной строки 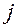на соответствующие функции

, .

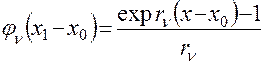При 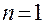функция с гибкой структурой имеет вид

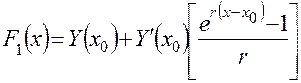, (4.19)

где 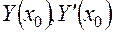– начальное значение функции 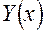и ее произ­водной в точке 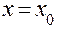; 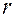– корень специального уравнения 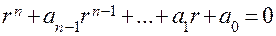, в рассматриваемом случае .

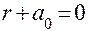Нахождение параметров функции 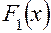связано с минимиза­цией базисной функции

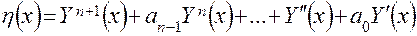. (4.20)

Далее представляется логичным определить порядок расчета параметров ФГС. В том случае, когда имеется всего один фактор, базисная функция имеет вид

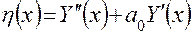. (4.21)

При 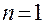на рассматриваемом отрезке функция равна нулю, и если проинтегрировать выражение (2.4.21) для того, чтобы избавиться от производных, можно получить

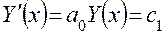. (4.22)

Подставляя в это уравнение значение начальной точки, легко установить, что величина первой производной связана со значени­ем величины 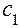и 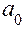соотношением . (4.23)

Если проинтегрировать уравнение (22) еще раз, то можно запи­сать выражение вида

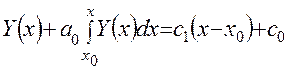. (4.24)

При условии, что 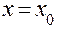, определяется 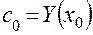. Тогда уравне­ние (4.24) целесообразно представить следующей зависимостью:

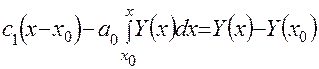. (4.25)

Из этого уравнения видно, что оно содержит неизвестные величи­ны. Теперь значение интеграла можно вычислить, так как функ­ция 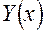УМ задана таблицей, а для определения 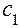и 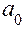можно образовать систему двух уравнений с двумя неизвестными на основе уравнения (4.25). Это нетрудно сделать, если подставить в (4.25) значение еще двух точек, взятых из временного ряда. Тогда

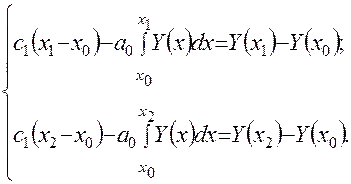(4.26)

После вычисления данных интегралов находятся неизвестные коэффициенты 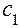и 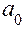. Затем определяется значение первой про­изводной путем подстановки в уравнение (4.23) 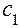, 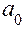и 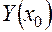. Ко­рень базисного уравнения равен параметру 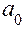со знаком минус. Вычисленные параметры подставляются в формулу ФГС (4.19) для получения математического выражения формы связи между 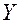и .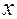

В качестве примера применения функции с гибкой структурой для прогнозирования в военном деле рассматривается задача по определению вида зависимости между коэффициентом выпуска серийных образцов условных технических систем и объемом задач, выполняемых с помощью данных образцов. Эта зависимость в дальнейшем используется для получения прогноза. Исходные данные представлены в табл. 1.

Таблица 1

	0,597	0,597	0,608	0,618	0,615	0,618	0,631
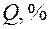
	31,2	32,3	33,4	34,3	34,5	35,5	37,8

Из этой таблицы выбираются значения трех опорных точек, одна из которых (начальное значение) должна лежать в середине ряда с тем, чтобы полученная функция одинаково точно прибли­жала данное значение как в конце, так и в начале ряда. Следовательно,

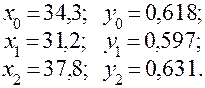
Определяются коэффициенты уравнения (4.26):

Следующий шаг – переход к вычислению необходимых интегралов (рис. 4.5).

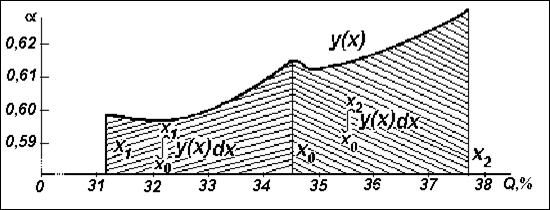
Рис. 4.5. Определение необходимых интегралов для ФГС

Интеграл вида 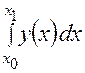есть площадь, ограниченная графиком и значениями 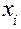, равными 34,3 и 31,2. Так как верхний предел ин­теграла меньше нижнего, то значение интеграла отрицательное. Площадь, ограниченная значениями 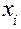равными 34,3 и 31,2, будет складываться из площадей трех трапеций:

.

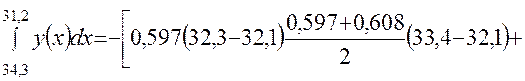
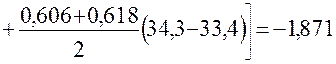Значение интеграла 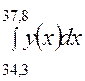будет

.

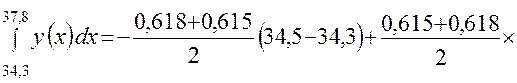
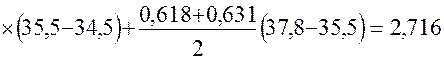Полученные коэффициенты подставляются в систему уравне­ний (4.26):

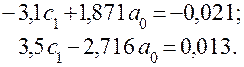
Решая эту систему, определяются

.

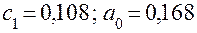Затем находится значение первой производной в начальной точ­ке путем подстановки в уравнение (4.23) вычисленных коэффици­ентов и .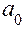

Тогда

.

Для 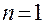базисное уравнение имеет вид

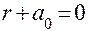или .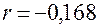

Таким образом, получены все параметры. Подставив в уравне­ние функции с гибкой структурой значение первой производной и значение 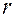, можно получить

.

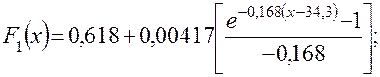
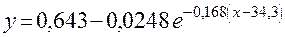Подстановкой вместо 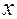его перспективного значения на определен­ный год определяется ожидаемая величина коэффициента выпуска. Необходимо отметить, что основной задачей при использовании ФГС для прогноза является определение корней базисного урав­нения 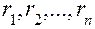, значения которых зависят от коэффициентов . Последние должны определяться из принципа оптимальной аппроксимации, заключающегося в минимизации остатка 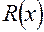и установлении таких значений коэффициентов 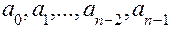, для которых значение остатка в каждой точ­ке таблицы исходных данных не превышает некоторой заданной величины (ошибки аппроксимации). При машинной реализации метода, базирующегося на применении ФГС, необходимо прини­мать допущение о дифференцируемости функции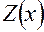 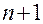раз, с учетом которого можно записать, что

; (4.27)

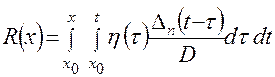, (4.28)

где 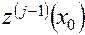– значение производной функции 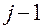поряд­ка в точке ;

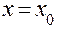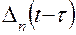– выражение, получаемое из определителя

(4.29)

заменой последней строки определителя на функции вида , ;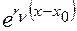

. (4.30)

Значения коэффициентов определяются в резуль­тате решения уравнения (4.30) путем приравнивания его к нулю. В связи с тем, что производные 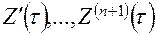неизвестны, пе­реходят к системе линейных алгебраических уравнений [1], [2] вида

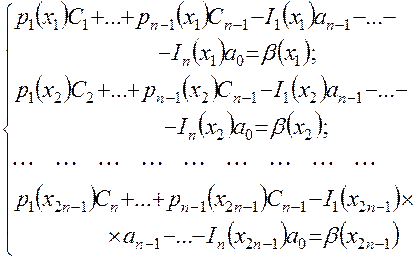, (4.31)

где , ;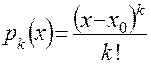

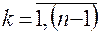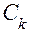– постоянная интегрирования; ;

, , ;

; .

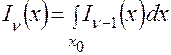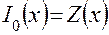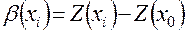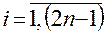Результатом решения этой системы является определение коэффи­циентов , что позволяет по базисному уравнению вычислить параметры 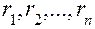. Неизвестные 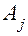как следует из (4.18), (4.27), равны значениям производных функций в точке 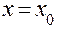, то есть

.

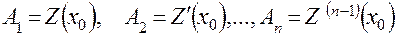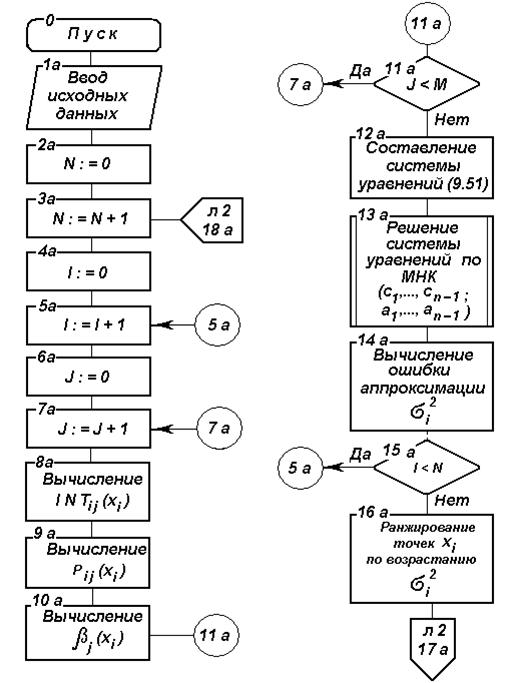
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС

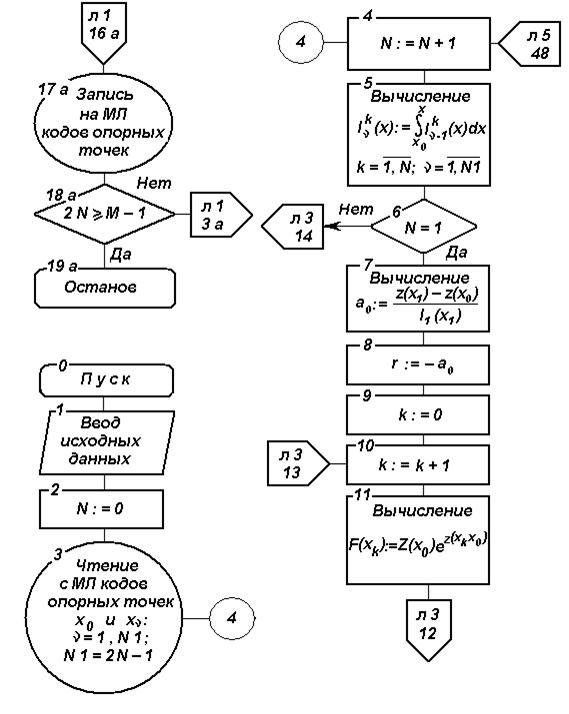
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

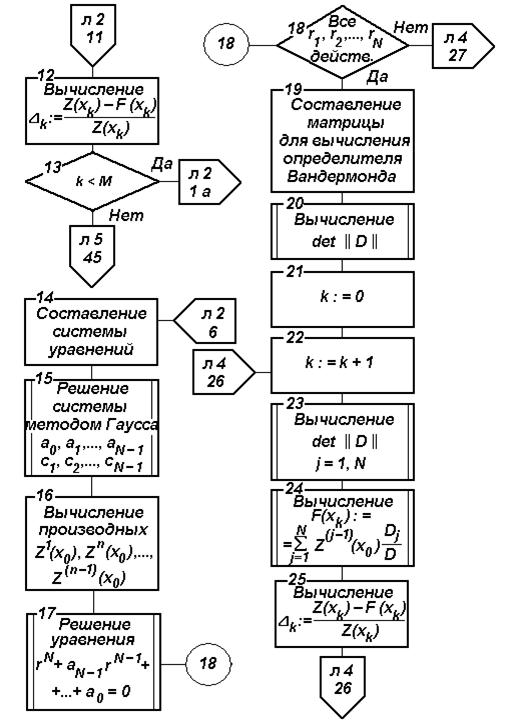
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

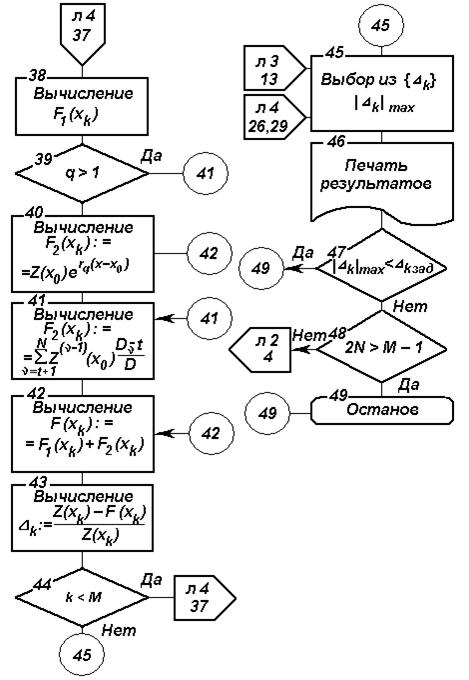
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

На основе изложенного разработан алгоритм параметрического прогнозирования, блок-схема которого изображена на рис. 4.6.

Согласно работам [1], [2] можно утверждать, что ошибка ап­проксимации в значительной степени зависит от системы опорных точек и , которые необходимо выбрать для вычисления коэффициентов при неизвестных 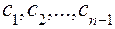и 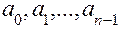и свободных членов системы уравнений (31). По­этому в рамках алгоритма имеется специальная процедура выбора системы опорных точек (блоки 1–19), использование которой обе­спечивает минимальную ошибку аппроксимации. Смысл этой про­цедуры сводится к следующему:

· в качестве начальной точки последовательно выбирается каждая точка 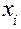таблицы исходных данных (блоки 4а, 5а, 15а);

· при зафиксированном значении 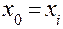вычисляются значения 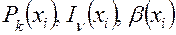(блоки 6а–11а);

· составляется система уравнений (4.31) (блок 12а);

· решается система уравнений (4.31) по МНК и определяются значения Си 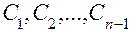, 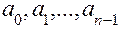(блок 13а);

· устанавливается структура модели, например в виде регресси­онного уравнения

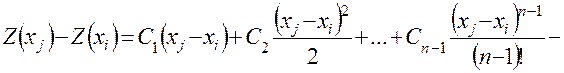
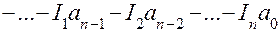(4.32)

параметры которого определены выше, и задают ошибку аппрок­симации по зависимости (блок 14а)

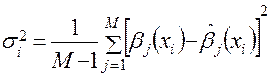, (4.33)

где 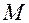– число наблюдений над прогнозируемой характеристикой;

· осуществляются ранжировка исходных данных по возраста­нию 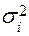, выбор опорных точек по правилу (блок 16а)

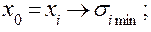
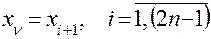
и их запись;

· описанная процедура повторяется для каждого значения (бло­ки 2а, За, 18а).

После выбора опорных точек в алгоритме предусмотрены опе­раторы по подготовке к составлению системы уравнений 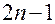порядка. С этой целью по соответствующим зависимостям методом численного интегрирования (методом трапеций) вычисляются 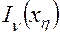, а также значения 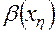и 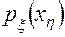(блок 5). При этом

.

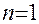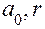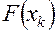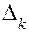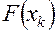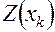Если число членов ФГС-модели , то значения параметров функции и относительного отклонения функции от в 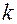-й точке рассчитываются в соответ­ствии с выражениями блоков 7–3. На основе выбора из множе­ства 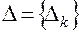значения 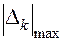и сравнения его с заданным 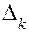(блоки 45, 47), принимается решение либо продолжать усложнять модель, либо удовлетвориться достигнутой сложностью. При 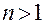осуществляется составление системы уравнений 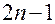по­рядка вида (4.31) (блок 14) и решение ее методом Гаусса относи­тельно параметров 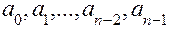и постоянных интегриро­вания 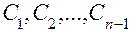(блок 15).

В блоке 16 осуществляется вы­числение параметров

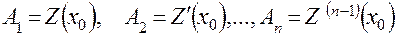
по зависимостям

(4.34)

Вычисление корней 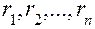базисного уравнения произво­дится методом Ньютона с использованием стандартной програм­мы (блок 17). Поскольку в общем случае корни уравнения могут быть действительными, комплексными или действительными и комплексными, в блоках 18, 27 производится их анализ с целью определения дальнейшей расчетной схемы. При условии, что все корни 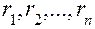действительные, функция 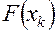принимает вид

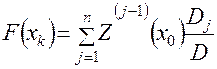, (4.35)

где 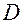– степенной определитель 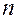-го порядка (4.29), значение которого вычисляется методом перекрестно­го умножения (блоки 19, 20);

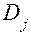– определитель, получаемый из (4.29) заменой 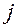-й строки на функции 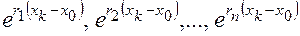– блок 23;

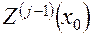– вычисленная ранее производная.

Значение функции в каждой точке и ее отклонения 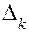вычисля­ются в блоках 21, 22, 24-26. При подстановке значени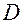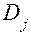й , и 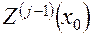зависимость (4.35) принимает вид суперпозиции экспо­ненциальных законов, параметрами которых являются аргументы прогнозирующих зависимостей.

Если все корни 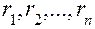комплексные, то 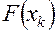имеет вид

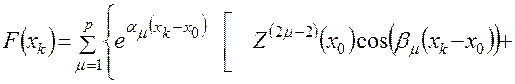
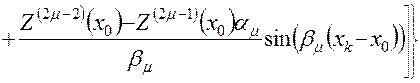,(4.36)

где 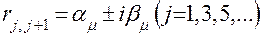– нечетное натуральное число;

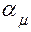– действительная часть корня; ; .

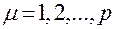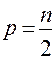Значения функции 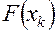и ее отклонения 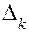вычисляются в блоках 28, 29. Если в результате анализа устанавливается, что 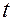корней 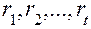комплексные, а 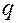корней дей­ствительные, то 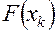принимает вид

,

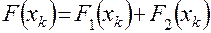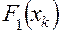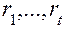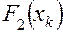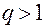где вычисляется по зависимости (4.36) с использованием корней блок 38); при вычисляется по за­висимости (4.35) с использованием корней 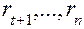(блоки 33, 34, 35, 41), при 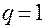– в соответствии с блоками 32, 39, 40. Зна­чения функции 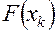и ее отклонения 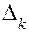от 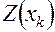вычисляются в блоках 36, 37, 42, 43, 44. Результаты расчетов выводятся на пе­чать. После вычисления функци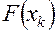и и 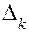в каждом из приве­денных случаев выбирается максимальное значение отклонения 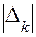, которое сравнивается с заданным (блоки 45, 47).

По результатам сравнения принимается решение о наращива­нии сложности модели 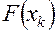либо о его прекращении. В блоке 48 осуществляется проверка достаточности числа наблюдений для за­данной сложности модели.

Вопросы для самопроверки к разделу 2

1. В чем сущность метода статистических испытаний?

2. Что понимается под названием вычислительный эксперимент?

3. Что представляет собой статистическое моделирование?

4. Какие основные составные части метода статистических испытаний Вы знаете?

5. Какие основные достоинства метода статистических испытаний Вы знаете?

6. Каким образом возможно моделирование системы массового обслуживания?

7. Что такое однофазная система обслуживания?

8. Каким образом происходит оценка результатов наблюдений при моделировании?

9. В чем суть метода повторений?

10. В чем суть метода подынтервалов?

11. Какие прикладные задачи имитационного моделирования Вы знаете?

12. В чем суть метода экспоненциального сглаживания?

Раздел 3. Оценка качества моделей. Планирование вычислительного эксперимента

Date: 2015-05-23; view: 900; Нарушение авторских прав