
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Анализ результатов испытаний. Завершающим этапом испытаний по полному или дробному факторному плану является статистический анализ полученных данных
|
|
Завершающим этапом испытаний по полному или дробному факторному плану является статистический анализ полученных данных, который включает: оценку воспроизводимости результатов испытаний; оценку значимости коэффициентов регрессии и уточнение вида модели; проверку адекватности модели.
Целью проверки воспроизводимости является установление однородности результатов испытаний, проводимых на различных уровнях 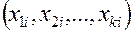 . В ходе опытно-конструкторских работ при проведении лабораторных и стендовых испытаний обычно используется освоенная аппаратура, обеспечивающая стабильность условий. Поэтому предварительное заключение относительно воспроизводимости ожидаемых результатов часто может быть сделано до начала испытаний. При необходимости проверки воспроизводимости содержание задачи совпадает с задачей проверки гипотезы о стабильности условий испытаний. Пусть результаты испытаний представлены, как показано в табл. 7.
. В ходе опытно-конструкторских работ при проведении лабораторных и стендовых испытаний обычно используется освоенная аппаратура, обеспечивающая стабильность условий. Поэтому предварительное заключение относительно воспроизводимости ожидаемых результатов часто может быть сделано до начала испытаний. При необходимости проверки воспроизводимости содержание задачи совпадает с задачей проверки гипотезы о стабильности условий испытаний. Пусть результаты испытаний представлены, как показано в табл. 7.
Проверке подлежит гипотеза 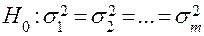 , где –
, где – 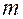 количество строк матрицы планирования. Условием проверки гипотезы является наличие параллельных опытов в каждой из строк.
количество строк матрицы планирования. Условием проверки гипотезы является наличие параллельных опытов в каждой из строк.
Тогда в каждой строке могут быть вычислены
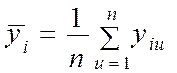 ;
; 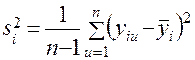 ;
; 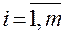 ,
,
где 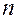 – количество повторных испытаний.
– количество повторных испытаний.
Таблица 7
| Номер опыта | План испытаний | Результаты испытаний | Вычисляемые оценки | ||||||||

| 
| 
| 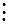
| 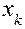
| 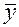
| 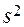
| |||||
| + | – | – | ... | + | 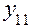
| 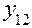
| ... | 
| 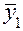
| 
| |
| + | – | + | ... | + | 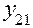
| 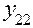
| ... | 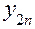
| 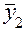
| 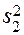
| |
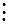
| 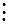
| 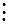
| 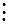
| 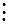
| 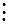
| 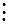
| 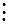
| ... | 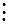
| 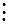
| 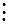
|
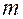
| + | – | + | ... | – | 
| 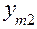
| ... | 
| 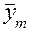
| 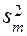
|
Для проверки гипотезы можно воспользоваться критериями Кохрена или Бартлетта. Если 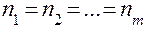 , расчетное значение статистики критерия Кохрена определяется по формуле и гипотеза
, расчетное значение статистики критерия Кохрена определяется по формуле и гипотеза 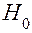 принимается, если
принимается, если 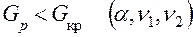 , где
, где 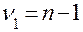 ,
, 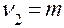 . Если дисперсии
. Если дисперсии 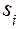 однородны (принята гипотеза
однородны (принята гипотеза 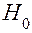 ), то дисперсия опыта (или, что то же самое, дисперсия воспроизводимости) подсчитывается по зависимости
), то дисперсия опыта (или, что то же самое, дисперсия воспроизводимости) подсчитывается по зависимости
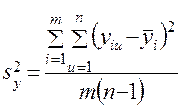 , (11)
, (11)
где знаменатель характеризует число степеней свободы 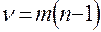 . В общем случае,
. В общем случае, 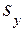 подсчитывается как среднее взвешенное значение
подсчитывается как среднее взвешенное значение
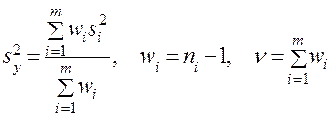 . (12)
. (12)
Проверка значимости коэффициентов регрессии позволяет лучше осмыслить математическое описание процесса, а также уточнить вид модели путем отсеивания факторов, слабо влияющих на значение выходного параметра. Проверка значимости каждого из коэффициентов производится независимо, с помощью проверки гипотезы 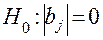 0 по
0 по 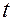 -критерию. Расчетные значения статистики критерия можно определить по соотношению
-критерию. Расчетные значения статистики критерия можно определить по соотношению
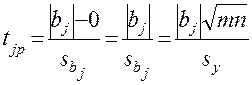 . (13)
. (13)
Если 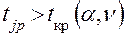 ,
, 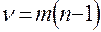 то коэффициент
то коэффициент 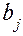 является значимым и соответствующий фактор оказывает существенное влияние на величину
является значимым и соответствующий фактор оказывает существенное влияние на величину 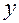 . Статистическая незначимость
. Статистическая незначимость 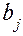 может быть вызвана следующими причинами:
может быть вызвана следующими причинами:
· интервал варьирования 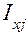 был выбран слишком малым;
был выбран слишком малым;
· уровень начального режима по фактору 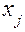 оказался близок к точке частного экстремума
оказался близок к точке частного экстремума 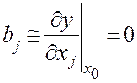 ;
;
· велика ошибка опыта из-за влияния неуправляемых и неконтролируемых факторов;
· данный фактор (совокупность факторов) не оказывают заметного влияния на величину выходного параметра.
Поскольку план ортогонален и коэффициенты оцениваются независимо друг от друга, оказавшиеся незначимыми коэффициенты могут быть отброшены без пересчета остальных.
Проверка адекватности заключается в подтверждении предположения, что полученная математическая модель достаточно верно описывает характер процесса. Формальное содержание гипотезы состоит в том, что предсказанные уравнением (расчетные) значения выходного параметра 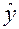 отклоняются от опытных
отклоняются от опытных 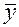 на величину, не превышающую некоторый наперед заданный уровень, и модель пригодна для обоснования инженерных решений. Для проверки гипотезы оценивается дисперсия адекватности
на величину, не превышающую некоторый наперед заданный уровень, и модель пригодна для обоснования инженерных решений. Для проверки гипотезы оценивается дисперсия адекватности
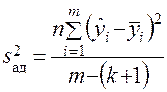 ;
;  . (14)
. (14)
Если дисперсия адекватности не превышает дисперсии опыта 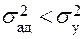 , то есть основание полагать, что модель адекватно описывает процесс. Согласно п. 1.3 для проверки гипотезы о дисперсиях используется
, то есть основание полагать, что модель адекватно описывает процесс. Согласно п. 1.3 для проверки гипотезы о дисперсиях используется 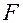 -критерий. Статистика критерия
-критерий. Статистика критерия
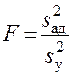 . (15)
. (15)
Модель считается адекватной процессу, если 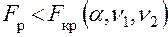 , где
, где 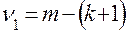 ,
, 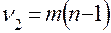 . Если
. Если 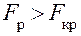 ,то для получения адекватного описания необходимо увеличить порядок аппроксимирующего полинома. Очевидно, что проверка адекватности возможна лишь в том случае, если
,то для получения адекватного описания необходимо увеличить порядок аппроксимирующего полинома. Очевидно, что проверка адекватности возможна лишь в том случае, если 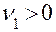 , то есть число разных испытаний
, то есть число разных испытаний 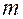 превосходит количество включаемых в модель факторов.
превосходит количество включаемых в модель факторов.
Если гипотеза адекватности принимается, то модель может использоваться для управления процессом (при доводочных испытаниях для определения значений факторов, при которых достигается экстремальное или заданное значение выходного параметра). Незначимые коэффициенты могут быть отброшены, однако при этом необходима основанная на анализе физической сущности явления уверенность, что эти факторы не влияют на выходной параметр. В противном случае следует стремиться продолжить испытания (расширив, если позволяют технические возможности,  по незначимым факторам).
по незначимым факторам).
Если модель неадекватна, возможны следующие решения: перейти к модели более высокого порядка (когда можно предположить, что опыты проводились в области, близкой к оптимальной); продолжить испытания, уменьшив интервал варьирования, или перенося центр плана в другую точку.
Рассмотрим примеры использования ДФП при организации испытаний технических систем.
1. Планируются испытания двигателя на надежность при эксплуатации. В качестве основных эксплуатационных факторов выделены: механические воздействия при транспортировании, воспроизводимые на вибростенде  , температура
, температура  и влажность воздуха
и влажность воздуха  , имитируемые попеременным термостатированием и выдержкой в термобарокамере; старение при хранении, достигаемое проведением ускоренных испытаний узлов двигателя
, имитируемые попеременным термостатированием и выдержкой в термобарокамере; старение при хранении, достигаемое проведением ускоренных испытаний узлов двигателя 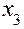 ; излучение и прогрев элементов
; излучение и прогрев элементов 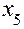 , с помощью секционных термобарокамер, с использованием электронагревательных приборов и холодильной установки. В качестве выходного параметра оценивалась величина давления в блоке цилиндров двигателя
, с помощью секционных термобарокамер, с использованием электронагревательных приборов и холодильной установки. В качестве выходного параметра оценивалась величина давления в блоке цилиндров двигателя 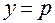 . Для испытаний выделялось
. Для испытаний выделялось 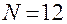 двигателей. Поскольку для полного учета всех факторов (при числе уровней
двигателей. Поскольку для полного учета всех факторов (при числе уровней  ) необходимо
) необходимо 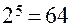 образца, было принято решение применить ДФП
образца, было принято решение применить ДФП 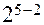 , причем
, причем 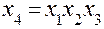 ,
, 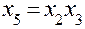 . Тогда обобщенный определяющий контраст
. Тогда обобщенный определяющий контраст 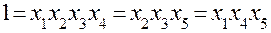 . Получаемая в этом случае математическая модель принимает вид
. Получаемая в этом случае математическая модель принимает вид
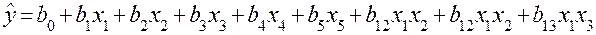 .
.
Поскольку реализация плана 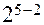 возможна при
возможна при 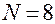 , оставшиеся четыре образца использовались для проведения контрольной серии испытаний. План испытаний показан в табл. 8.
, оставшиеся четыре образца использовались для проведения контрольной серии испытаний. План испытаний показан в табл. 8.
2. Планируются испытания двигателя, проводимые с целью эмпирического определения коэффициента усиления, величина которого в общем виде представляется как 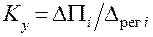 , где
, где 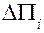 – изменение
– изменение 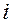 -го регулируемого выходного параметра двигателя,
-го регулируемого выходного параметра двигателя, 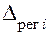 – изменение регулирующего параметра по
– изменение регулирующего параметра по 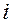 -му каналу регулирования. Исполнительными органами систем регулирования являются регуляторы расхода, регуляторы давления, дроссели. Величина
-му каналу регулирования. Исполнительными органами систем регулирования являются регуляторы расхода, регуляторы давления, дроссели. Величина 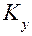 обычно включается в ТЗ на разработку.
обычно включается в ТЗ на разработку.
Таблица 8
| Номер опыта | 
| 
| 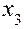
| 
| 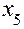
| Номер опыта | 
| 
| 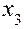
| 
| 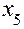
|
| – | – | – | – | + | – | + | + | – | + | ||
| + | – | – | + | + | + | + | + | + | + | ||
| – | + | – | + | – | + | + | + | + | + | ||
| + | + | – | – | – | |||||||
| – | – | + | + | – | – | – | – | – | + | ||
| + | – | + | – | – | – | + | – | + | – |
Из практики опытной отработки известно, что расчетные значения 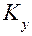 обычно не подтверждаются в ходе испытаний. Поэтому возникает потребность настройки регулирующих органов с последующей опытной проверкой. Для обеспечения эффективности организации работ по определению и настройке коэффициентов усиления по каналам регулирования двигателя находят применение полные и дробные факторные планы. Рассмотрим случай, в котором для проведения испытаний реализуется ПФП
обычно не подтверждаются в ходе испытаний. Поэтому возникает потребность настройки регулирующих органов с последующей опытной проверкой. Для обеспечения эффективности организации работ по определению и настройке коэффициентов усиления по каналам регулирования двигателя находят применение полные и дробные факторные планы. Рассмотрим случай, в котором для проведения испытаний реализуется ПФП 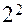 при числе испытаний
при числе испытаний 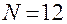 (табл. 8). В каждом испытании значения факторов
(табл. 8). В каждом испытании значения факторов  и
и  (
( и
и 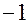 ) определяют крайние положения органов в выбранной области изменения этих факторов. Матрица планирования и полученные из опыта результаты представлены в табл. 9. В нижней строке таблицы приводятся вычисленные по формуле (8) значения коэффициентов
) определяют крайние положения органов в выбранной области изменения этих факторов. Матрица планирования и полученные из опыта результаты представлены в табл. 9. В нижней строке таблицы приводятся вычисленные по формуле (8) значения коэффициентов 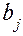
Таблица 9
| Режим | План | Результаты испытаний | 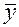
| 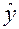
| ||||||

| 
| 
| 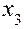
| 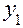
| 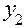
| 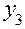
| 
| |||
| + | – | – | + | 0,7166 | 0,6769 | 0,7166 | 0,5785 | 0,6721 | 0,6939 | |
| + | – | + | – | 0,8100 | 0,8100 | 0,8700 | 0,7545 | 0,8111 | 0,7893 | |
| + | + | – | – | 0,6615 | 0,6076 | 0,5250 | 0,6071 | 0,6003 | 0,6221 | |
| + | + | + | + | 0,6071 | 0,5533 | 0,4941 | 0,5375 | 0,5480 | 0,5263 | |
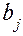
| 0,6578 | – 0,0837 | 0,0216 | – 0,0478 |
Рассмотрим порядок статистического анализа результатов испытаний. Для проверки условия воспроизводимости по формуле (11) определим
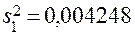 ;
; 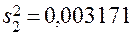 ;
; 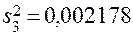 ;
; 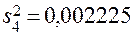 .
.
Затем вычислим расчетное значение статистики критерия Кохрена:
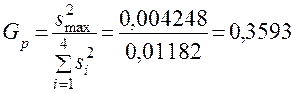 .
.
При уровне значимости 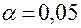 и числе степеней свободы
и числе степеней свободы  ,
, 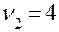 находим
находим 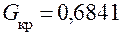 . Поскольку
. Поскольку 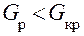 , принимается гипотеза об однородности данных (воспроизводимости результатов испытаний). Следовательно, дисперсия испытаний может быть определена по всем испытаниям согласно зависимости (12):
, принимается гипотеза об однородности данных (воспроизводимости результатов испытаний). Следовательно, дисперсия испытаний может быть определена по всем испытаниям согласно зависимости (12):
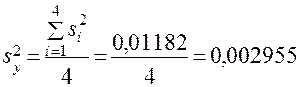 .
.
Из (9) видно, что погрешность оценивания
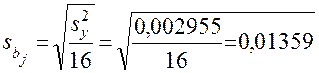 .
.
Для проверки значимости коэффициентов 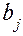 и уточнения вида модели вычислим расчетные значения статистики
и уточнения вида модели вычислим расчетные значения статистики 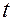 -критерия по формуле (13):
-критерия по формуле (13):
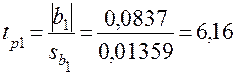 ;
; 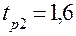 ;
; 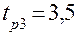 .
.
Из таблицы Приложения при 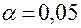 и
и 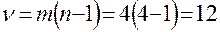 получим
получим 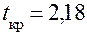 . Следовательно, для
. Следовательно, для 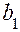 и
и 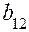 имеет место
имеет место  и эти коэффициенты значимо отличаются от нуля. Поскольку
и эти коэффициенты значимо отличаются от нуля. Поскольку 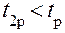 коэффициент
коэффициент  оказался незначимым. Поэтому фактор
оказался незначимым. Поэтому фактор  из дальнейшего рассмотрения исключаем. Уточненная модель принимает вид
из дальнейшего рассмотрения исключаем. Уточненная модель принимает вид
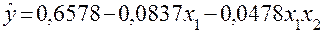 .
.
Для проверки адекватности модели определим предсказанные этой моделью значения 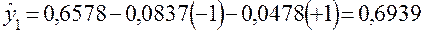 ;
; 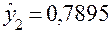 ;
;  ;
; 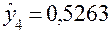 . Согласно зависимости (14) мера неадекватности модели оценивается дисперсией
. Согласно зависимости (14) мера неадекватности модели оценивается дисперсией
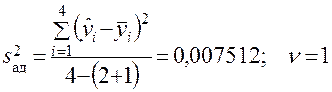 .
.
Тогда определяемое по (15) расчетное значение статистики критерия
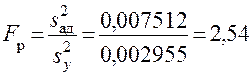 .
.
При 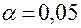 ,
, 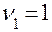 ,
, 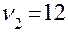 находим
находим 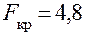 , что позволяет принять гипотезу об адекватности модели изучаемому процессу и использовать ее в дальнейшем для настройки двигателя.
, что позволяет принять гипотезу об адекватности модели изучаемому процессу и использовать ее в дальнейшем для настройки двигателя.
Оптимальные планы
Если целью испытаний является изучение характера процесса, то с получением адекватной модели они могут быть завершены. При доводочных испытаниях, когда 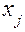 – параметры конструкции, работа продолжается для получения координат точки
– параметры конструкции, работа продолжается для получения координат точки 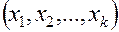 в которой
в которой 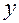 соответствует заданному (или экстремальному) значению. Рассмотрим два основных подхода к отысканию области оптимума
соответствует заданному (или экстремальному) значению. Рассмотрим два основных подхода к отысканию области оптимума 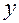 : крутое восхождение и симплексный метод.
: крутое восхождение и симплексный метод.
Крутое восхождение (метод Бокса-Уилсона) выгодно отличается от традиционной организации многофакторного эксперимента, при проведении которого последовательно отыскивается экстремум по каждому из факторов. Сущность крутого восхождения заключается в шаговом движении в направлении наибольшего изменения функции (направлении градиента)
 ,
, 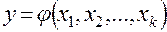 (16)
(16)
с корректировкой этого направления после достижения частного экстремума функции. На пути движения к экстремуму производится регулярный статистический анализ. В (16) 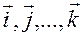 – единичные векторы в направлении координатных осей.
– единичные векторы в направлении координатных осей.
Определению 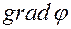 служит реализация ПФП (ДФП), обеспечивающая получение адекватной модели чаще всего в виде линейного уравнения регрессии. Дальнейшие операции сводятся к следующему.
служит реализация ПФП (ДФП), обеспечивающая получение адекватной модели чаще всего в виде линейного уравнения регрессии. Дальнейшие операции сводятся к следующему.
Вычисляются произведения 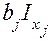 . Фактор, для которого имеет место
. Фактор, для которого имеет место 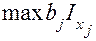 принимается за базовый
принимается за базовый 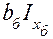 . Для базового фактора исходя из анализа физической сущности процесса устанавливается шаг варьирования
. Для базового фактора исходя из анализа физической сущности процесса устанавливается шаг варьирования 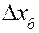 (в направлении экстремума), после чего для других
(в направлении экстремума), после чего для других  шаг рассчитывается пропорционально наклону поверхности отклика, характеризующемуся величиной
шаг рассчитывается пропорционально наклону поверхности отклика, характеризующемуся величиной 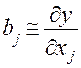 :
:
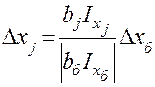 . (17)
. (17)
Затем производятся «мысленные опыты», которые заключаются в вычислении предсказываемых уравнением регрессии значений 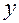 в точках факторного пространства. Через несколько (обычно два – пять) шагов
в точках факторного пространства. Через несколько (обычно два – пять) шагов
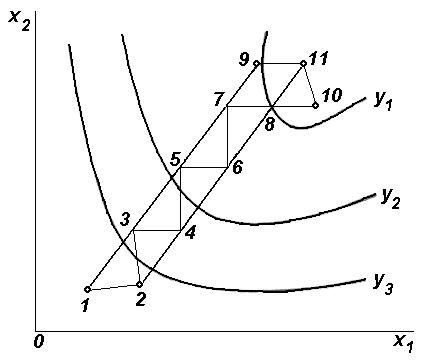
Рис. 2. Графическое представление проведения испытаний по схеме крутого
восхождения
проводятся реальные испытания. Сравнивая опытные значения с расчетными, определяют наиболее близкие к экстремальным значения 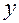 , где и проводится новая серия испытаний, после чего при необходимости крутое восхождение продолжается. Испытания прекращаются, когда все или почти все значения
, где и проводится новая серия испытаний, после чего при необходимости крутое восхождение продолжается. Испытания прекращаются, когда все или почти все значения 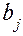 незначимы или близки к нулю.
незначимы или близки к нулю.
Пример проведения испытаний по схеме крутого восхождения содержится в табл. 10.
В качестве параметра оптимизации рассматривалась удельная тяга ЖРД – 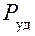 , максимума которой добивались подбором форсунок окислителя разного диаметра сопла
, максимума которой добивались подбором форсунок окислителя разного диаметра сопла  – фактор
– фактор  и изменением выходного сечения сопла
и изменением выходного сечения сопла 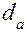 – фактор
– фактор  . Предварительно по ПФП
. Предварительно по ПФП 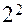 получена модель, с помощью которой определено градиентное направление
получена модель, с помощью которой определено градиентное направление  . В дальнейшем проведение реальных испытаний чередовалось с мысленными
. В дальнейшем проведение реальных испытаний чередовалось с мысленными
Таблица 10
| Уровень | 
| 
| |||||
| мм | |||||||
| Основной………………………… Интервал…………………………. Нижний…………………………... Верхний………………………….. | 4,5 0,2 4,3 4,7 | ||||||
Коэффициент  …………
Шаг при …………
Шаг при 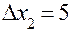 ………………. ……………….
| 1,2 0,1 | 0,8 | 
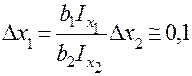
| ||||
| Номер опыта | Вид испытания | 
| 
| 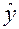
| 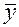
| ||
| мм | н∙с/кг | ||||||
| Начальная точка………….... Мысленный опыт………….. Реализованный…………….. Мысленный………………... Реализованный ……………. Реализованный……………. | 4,7 4,8 4,9 5,0 5,1 5,2 | – – – | – – – | ||||
опытами. При подсчете предсказанных значений 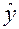 натуральные значения
натуральные значения 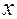 переводились в кодированные по формуле. Как видно из табл. 2.11, переход от условий испытаний № 5 к условиям испытания № 6 не обеспечивает приращения удельной тяги. Далее в точке
переводились в кодированные по формуле. Как видно из табл. 2.11, переход от условий испытаний № 5 к условиям испытания № 6 не обеспечивает приращения удельной тяги. Далее в точке 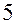 (рис. 3.2) была проведена контрольная серия из четырех испытаний, которая подтвердила, что дальнейшие вариации
(рис. 3.2) была проведена контрольная серия из четырех испытаний, которая подтвердила, что дальнейшие вариации  и
и 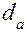 не ведут к увеличению
не ведут к увеличению 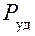 .
.
Симплексный метод заключается в том, что испытания проводятся в точках факторного пространства, соответствующих вершинам симплексов. Под 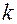 -мерным симплексом подразумевают выпуклую геометрическую фигуру, имеющую
-мерным симплексом подразумевают выпуклую геометрическую фигуру, имеющую 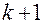 вершину, соединенные прямыми отрезками-ребрами. Одномерным симплексом будет отрезок прямой, двумерным – плоский треугольник, трехмерным – тетраэдр и т.д. При планировании испытаний обычно используют правильные симплексы, у которых вершины находятся друг от друга на одинаковом расстоянии. В отличие от крутого восхождения, при использовании симплексного метода процесс изучения поверхности отклика совмещается с движением к экстремуму. Схема поиска экстремума симплекс-методом при
вершину, соединенные прямыми отрезками-ребрами. Одномерным симплексом будет отрезок прямой, двумерным – плоский треугольник, трехмерным – тетраэдр и т.д. При планировании испытаний обычно используют правильные симплексы, у которых вершины находятся друг от друга на одинаковом расстоянии. В отличие от крутого восхождения, при использовании симплексного метода процесс изучения поверхности отклика совмещается с движением к экстремуму. Схема поиска экстремума симплекс-методом при 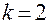 показана на рис. 2. Сначала проводится серия испытаний в вершинах правильного
показана на рис. 2. Сначала проводится серия испытаний в вершинах правильного 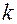 -мерного симплекса (точки
-мерного симплекса (точки 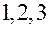 ) с целью выявить точку, характеризующую условия, при которых получаются худшие результаты. Следующую серию испытаний проводят в вершинах нового симплекса, который получают заменой точки, соответствующей худшему результату (точка
) с целью выявить точку, характеризующую условия, при которых получаются худшие результаты. Следующую серию испытаний проводят в вершинах нового симплекса, который получают заменой точки, соответствующей худшему результату (точка 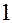 ), ее зеркальным отображением. Тем самым достигается смещение центра тяжести симплекса в направлении экстремума. В дальнейшем процедура повторяется, и образуется последовательность симплексов, перемещающихся в факторном пространстве в направлении к экстремуму. На близость экстремума указывает начинающееся вращение симплекса вокруг одной из его вершин.
), ее зеркальным отображением. Тем самым достигается смещение центра тяжести симплекса в направлении экстремума. В дальнейшем процедура повторяется, и образуется последовательность симплексов, перемещающихся в факторном пространстве в направлении к экстремуму. На близость экстремума указывает начинающееся вращение симплекса вокруг одной из его вершин.
Шаговое движение к экстремуму продолжается до тех пор, пока будет достигнута «почти стационарная область», которая не может быть описана линейной моделью, и где значимы совместные (квадратичные) эффекты воздействия.
Близость «почти стационарной области» можно установить, если провести серию испытаний в центре плана и определить значение выходного параметра 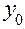 . Вычисляемое для линейной модели значение
. Вычисляемое для линейной модели значение 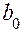 при реализации ПФП или ДФП в «почти стационарной области» является совместной оценкой для свободного члена и суммы квадратов членов. Следовательно, разность
при реализации ПФП или ДФП в «почти стационарной области» является совместной оценкой для свободного члена и суммы квадратов членов. Следовательно, разность 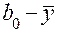 дает представление о кривизне поверхности отклика.
дает представление о кривизне поверхности отклика.
«Почти стационарную область» в большинстве случаев с приемлемой точностью можно описать уравнением второго порядка
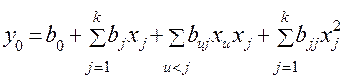 . (18)
. (18)
Поскольку для отыскания раздельных оценок параметров число уровней должно быть на единицу больше степени полинома, число уровней должно быть не менее трех. Однако применение ПФП типа 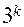 приведет к резкому возрастанию количества испытаний. Для сокращения
приведет к резкому возрастанию количества испытаний. Для сокращения  можно использовать центральные композиционные планы (ЦКП). Ядро ЦКП составляют ПФП или ДФП: ПФП, если число факторов
можно использовать центральные композиционные планы (ЦКП). Ядро ЦКП составляют ПФП или ДФП: ПФП, если число факторов 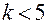 , и ДФП при
, и ДФП при 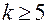 . Это приводит к тому, что если после реализации ПФП (ДФП) гипотеза о линейности модели не подтвердилась, нет необходимости проводить испытания заново. Для получения модели второго порядка достаточно добавить к ПФП (ДФП) несколько специальным образом подобранных точек, в которых и провести дополнительную серию испытаний.
. Это приводит к тому, что если после реализации ПФП (ДФП) гипотеза о линейности модели не подтвердилась, нет необходимости проводить испытания заново. Для получения модели второго порядка достаточно добавить к ПФП (ДФП) несколько специальным образом подобранных точек, в которых и провести дополнительную серию испытаний.
Пусть для получения линейной модели реализован ПФП 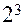 . Согласно рис. 1,б экспериментальные точки лежат в вершинах куба. Если линейная модель неадекватна, то в план включается
. Согласно рис. 1,б экспериментальные точки лежат в вершинах куба. Если линейная модель неадекватна, то в план включается 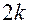 так называемых «звездных точек» с координатами
так называемых «звездных точек» с координатами 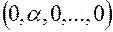 , расположенных на сфере диаметром
, расположенных на сфере диаметром 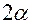 (рис. 3). Таким образом, каждая из точек плана лежит на координатных осях на расстоянии от центра плана, называемым звездным плечом
(рис. 3). Таким образом, каждая из точек плана лежит на координатных осях на расстоянии от центра плана, называемым звездным плечом 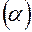 . Центром плана является центральная точка прямоугольника, если число факторов
. Центром плана является центральная точка прямоугольника, если число факторов 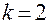 , куба при
, куба при 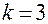 , гиперкуба, когда
, гиперкуба, когда 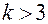 . Наличие звездных точек, собственно, и задает центральный композиционный план.
. Наличие звездных точек, собственно, и задает центральный композиционный план.
Представление о положении звездных точек в факторном пространстве дают следующие примеры: при 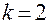 и ядре плана, образованном ПФП
и ядре плана, образованном ПФП 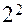 , величина звездного плеча
, величина звездного плеча 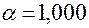 ; если
; если 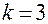 , а в ядре реализован ПФП
, а в ядре реализован ПФП 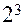 , то
, то 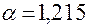 ; при
; при 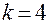 и ПФП
и ПФП 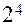
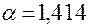 . Общее число испытаний при реализации ЦКП
. Общее число испытаний при реализации ЦКП
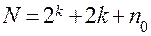 ,
,
где 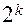 – ядро плана,
– ядро плана, 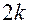 – число звездных точек;
– число звездных точек; 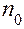 – количество испытаний, проводимых в центре плана.
– количество испытаний, проводимых в центре плана.
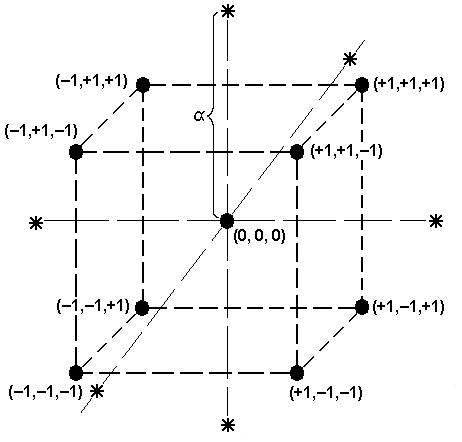
Рис. 3. «Звездные точки» с координатами
Пример ЦКП, в котором сохранено свойство ортогональности, приведен в табл. 11. В этом плане 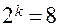 ,
, 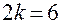 ,
, 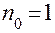 .
.
 Поскольку в ЦКП ортогональность обеспечивается, оценки коэффициентов получаются независимо. Однако дисперсии
Поскольку в ЦКП ортогональность обеспечивается, оценки коэффициентов получаются независимо. Однако дисперсии 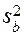 , как видно из приводимой расчетной зависимости, неодинаковы для разных коэффициентов:
, как видно из приводимой расчетной зависимости, неодинаковы для разных коэффициентов:
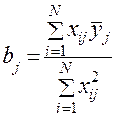 ; (19)
; (19)
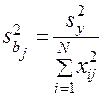 ;
; 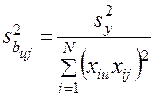 . (20)
. (20)
Таблица 11
| Номер опыта | 
| 
| 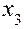
| Номер опыта | 
| 
| 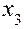
|
| – | – | – | 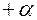
| ||||
| – | + | – | 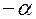
| ||||
| + | – | – | 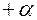
| ||||
| + | + | – | 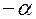
| ||||
| – | – | + | 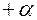
| ||||
| – | + | + | 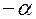
| ||||
| + | – | + | |||||
| + | + | + |
При реализации такого плана, как видно из табл. 11, 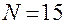 , в то время как для ПФП
, в то время как для ПФП 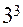
 .
.
Адекватная модель второго порядка может использоваться для нахождения оптимального значения факторов (в частном случае оптимальных конструктивных параметров).
Необходимо отметить, что кроме рассмотренных известно большое количество других методов оптимального планирования испытаний, развитых в специальной дисциплине — теории планирования эксперимента. К настоящему времени накоплен значительный опыт их использования при испытании составных частей технических систем, главным образом, в процессе опытно-конструкторских работ; известны пути приложения методов для оптимизации испытаний отдельных элементов образцов техники. Во всех случаях условием успешного планирования является правильное сочетание цели испытаний с возможностями выбранного метода и учет характера самого изучаемого явления.
Вопросы для самопроверки к разделу 3
1. Как происходит оценка качества модели?
2. Какие свойства модели Вы знаете?
3. В чем цель методов стратегического планирования имитационных экспериментов?
4. Какие методы повышения качества оценок показателей эффективности Вы знаете?
5. Какие основные этапы в общем случае можно выделить при выборе стратегии испытания?
6. Что такое полные факторные планы испытаний?
7. Что такое дробные факторные планы испытаний?
8. Что является целью проверки воспроизводимости?
Date: 2015-05-23; view: 783; Нарушение авторских прав