
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Событие, связанное с окончанием обслуживания
|
|
1. Проверка состояния очереди (пустая или непустая).
а) Если очередь пуста, объявить простой системы.
б) Если очередь непуста, то начать обслуживание первого по очереди клиента, уменьшить длину очереди на единицу и скорректировать протокол времени ожидания; получить время обслуживания клиента  и вычислить время окончания обслуживания (текущее время
и вычислить время окончания обслуживания (текущее время  ). Поскольку в этом примере система начинает работу при пустой очереди, она начинает функционировать с состояния простоя. Первая заявка на обслуживание поступает через
). Поскольку в этом примере система начинает работу при пустой очереди, она начинает функционировать с состояния простоя. Первая заявка на обслуживание поступает через
 ч.
ч.
Последовательность случайных чисел, используемая в данном примере, из следующего ряда
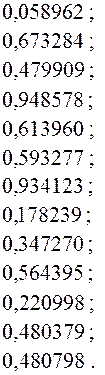
Таким образом, модель переходит из  в
в 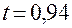 . В момент
. В момент 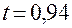 происходит событие, связанное с поступлением требования на обслуживание, поэтому, следуя приведенной выше схеме, вычисляем время поступления следующего требования:
происходит событие, связанное с поступлением требования на обслуживание, поэтому, следуя приведенной выше схеме, вычисляем время поступления следующего требования: 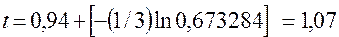 .
.
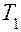 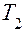 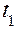
   Поступление Поступление Конец обслуживания Поступление Поступление Конец обслуживания
       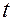
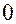 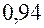  
|
Рис. 2.3. События, связанные с окончанием обслуживания
Теперь, поскольку система простаивает, начинается обслуживание текущего клиента; время его обслуживания, задаваемое 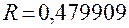 , равно
, равно 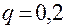 ч. Время окончания обслуживания вычисляется как
ч. Время окончания обслуживания вычисляется как
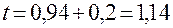 .
.
Система объявляется работающей, а время простоя корректируется следующим образом: Время простоя 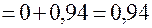 ч.
ч.
Осуществившиеся до настоящего момента события показаны на рис. 2.3.
Следующее по времени событие – поступление требования в момент 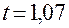 . Поскольку система продолжает работать, требование ставится в очередь, а длина очереди корректируется:
. Поскольку система продолжает работать, требование ставится в очередь, а длина очереди корректируется:
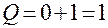 (в момент
(в момент 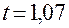 ).
).
Следующее требование поступает в момент времени
 .
.
(В рассматриваемом примере полезно наносить новые события на рис. 2.3 по мере их получения.)
Заметим, что все события, осуществившиеся в момент 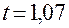 или ранее (рис. 2.3), относятся к предыстории, и их можно исключить из рассмотрения. Другими словами, в процессе моделирования необходимо хранить информацию лишь о будущем. Это замечание очень важно в связи с использованием ЭВМ, поскольку позволяет экономить память.
или ранее (рис. 2.3), относятся к предыстории, и их можно исключить из рассмотрения. Другими словами, в процессе моделирования необходимо хранить информацию лишь о будущем. Это замечание очень важно в связи с использованием ЭВМ, поскольку позволяет экономить память.
Следующее событие состоит в поступлении требования на обслуживание в момент 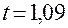 . Поскольку система все еще находится в рабочем состоянии, длина очереди должна быть скорректирована
. Поскольку система все еще находится в рабочем состоянии, длина очереди должна быть скорректирована
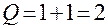 (в момент
(в момент 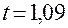 ),
),
а следующее требование поступит в момент
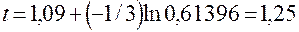 .
.
Следующее событие, происходящее в момент 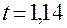 , представляет собой окончание обслуживания. Поскольку очередь непуста, начинается обслуживание первого по очереди клиента. Длина очереди изменяется
, представляет собой окончание обслуживания. Поскольку очередь непуста, начинается обслуживание первого по очереди клиента. Длина очереди изменяется
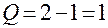 (в момент
(в момент 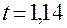 ),
),
а суммарное время ожидания становится равным
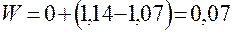 ч.
ч.
Используя 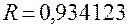 , получаем время завершения обслуживания данного клиента:
, получаем время завершения обслуживания данного клиента:
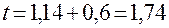 .
.
Теперь становится понятным, как получаются данные в ходе эксплуатации имитационной модели. Процедура повторяется до тех пор, пока не будет промоделирован весь интервал 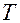 . После можно определить различные операционные характеристики, исходя из периода моделирования:
. После можно определить различные операционные характеристики, исходя из периода моделирования:
Доля времени простоя системы, % | = |
Суммарное время простоя
 Период моделирования Период моделирования 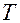
|
  100 100
| ||||||||

 Среднее время ожидания
клиентом обслуживания Среднее время ожидания
клиентом обслуживания
| = |
Суммарное время ожидания 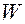
 Число поступающих клиентов Число поступающих клиентов
|
Вычисление средней длины очереди осуществляется несколько иначе. Из рис. 2.4 видно, каким образом обычно меняется длина очереди в зависимости от 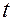 за моделируемый период времени продолжительности
за моделируемый период времени продолжительности 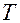 . Например, в рассматриваемой здесь обслуживающей системе длина очереди
. Например, в рассматриваемой здесь обслуживающей системе длина очереди 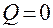 в период между
в период между  и
и 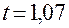 ,
, 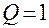 между
между 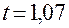 и
и 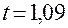 и
и 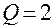 между
между 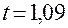 и
и 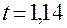 . Эта информация необходима для получения графика на рис. 4. Средняя длина очереди представляет собой среднее значение, изображенное пунктирной линией, то есть
. Эта информация необходима для получения графика на рис. 4. Средняя длина очереди представляет собой среднее значение, изображенное пунктирной линией, то есть
Средняя длина очереди 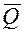 = =
|  Площадь Площадь 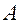 Моделируемый период
Моделируемый период 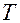
|
Заметим, что для получения 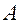 необязательно ждать истечения периода
необязательно ждать истечения периода 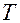 поскольку
поскольку 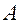 можно вычислять через приращения каждый раз, когда меняется
можно вычислять через приращения каждый раз, когда меняется 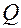 . Так, в данном примере
. Так, в данном примере 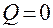 между
между  и
и 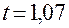 и
и 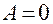 ;
; 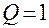 между
между 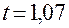 и
и 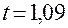 и, следовательно,
и, следовательно, 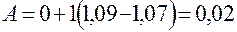 ;
; 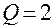 между
между 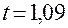 и
и 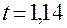 и
и 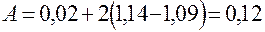 . Этот процесс приращений продолжается до тех пор, пока
. Этот процесс приращений продолжается до тех пор, пока 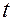 не станет равным
не станет равным 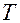 .
.
 | |||
 | |||


 Средняя длина очереди = A/t
Средняя длина очереди = A/t



 Площадь A
Площадь A
 |




Date: 2015-05-23; view: 583; Нарушение авторских прав