Метод исключения переменных

Рассмотрим задачу оптимизации, в которой требуется найти экстремум критерия оптимальности

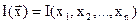(2.10)

при ограничении в виде равенства

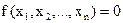. (2.11)

Экстремум, который достигается функцией с учётом выполнения соотношения (2.11), связывающего между собой независимые переменные, называется условным или относительным в отличие от безусловного экстремума, имеющего место при отсутствии ограничений.

Поставленную задачу можно решить следующим образом. Можно решить уравнение (2.11) относительно какой-либо переменной, например х_n, выразив его через остальные n-1 переменных х₁, х₂, …, х_n-1

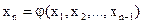. (2.12)

Подставляя затем это выражение в (2.10), получим функцию, которая будит зависеть только от переменных х_ί, 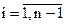, не связанных дополнительными условиями

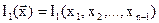. (2.13)

Таким образом, устраняя ограничивающее условие(2.11), удалось и уменьшить размерность исходной оптимальной задачи и свести задачу с ограничениями к эквивалентной задаче безусловной оптимизации, что позволяет применить для решения методы классического анализа.

Часто имеется несколько ограничений в виде равенств

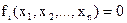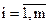, . (2.14)

В этом случае число связей (5.14) m меньше размерности n вектора искомых переменных х_ί. Требования m<n связано с тем, что в противном случае множество допустимых решений задачи представляет собой либо набор изолированных точек, являющихся корнями системы уравнений (5.14), либо вообще пусто. При m=n, если система (5.14) совместна, может оказаться, что система (2.14) имеет единственное решение и задача оптимизации не имеет смысла.

Если ранг матрицы Якоби равен m, т.е.

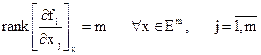, (2.12)

то m уравнений связи можно в простейших случаях разрешить относительно m переменных (например, х₁, х₂, …, х_m), выразив их через n-m остальных. Подстановка их в целевую функцию приводит к задаче на безусловный экстремум функции n-m переменных. Условие (2.12) является условием регулярности типа линейной независимости для задач на условный экстремум.

Выразим х₁, х₂, …, х_m через остальные n-m переменных

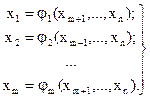(2.16)

Подставляя (2.16) в (2.10), получаем задачу безусловной оптимизации без ограничений:

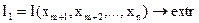. (2.17)

Решая задачу (2.17) находим и подставляя их в (2.16), находим оптимальные значения остальных переменных: х^*₁, х^*₂, …, х^*_m

При наличии нескольких ограничений в виде нелинейных уравнений практически затруднено и даже невыполнимо решение системы (2.14) относительно m переменных с целью их выражения через остальные n-m переменных и исключение таким образом ограничивающие условия. Поэтому данный метод имеет ограниченное применение и уступает по эффективности методам Лагранжа и штрафных функций.

Date: 2015-05-23; view: 1491; Нарушение авторских прав