Метод множителей Лагранжа

Рассмотрим задачу условной оптимизации с ограничением в виде равенств

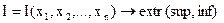(2.18)

при условии

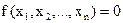. (2.19)

Предположим, что условие регулярности (2.12) выполняется, т.е.

Метод множителей Лагранжа заключается в следующем: составляют вспомогательную функцию 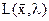, в которую входит уравнение связей (2.19)

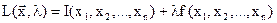. (2.20)

Функция L называется нормальной функцией Лагранжа, а коэффициент λ – неопределённым множителем Лагранжа (λ пока неизвестная величина).

Если в точке 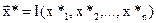функция достигает максимума (или минимума) при условии (2.19), то функция 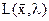так же достигает минимума (или максимума) по х в этой точке. При этом по переменной λ функция 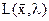достигает максимума (или минимума), т.е. точка 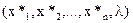является Седловой точкой функции .

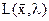Поэтому для решения задачи оптимизации определяем точку, в которой частные произведения равны нулю:

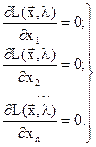(2.21)

Решив систему уравнений (2.21), определяем

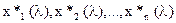, (2.22)

зависящие от неопределённого множителя λ. Чтобы определить значение λ, найдём и приравняем нулю частную производную 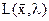по λ:

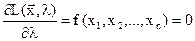. (2.23)

Подставим выражение (2.22) в уравнение (2.23)

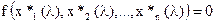. (2.24)

Отсюда определяем λ и подставляем его в выражение (2.22), окончательно находим экстремальную точку 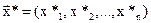. Подставляя 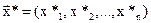в (2.18), можно вычислить экстремальное значение критериев .

Если имеется несколько ограничений в виде равенств, то каждому из этих ограничений соответствует свой множитель λ_і Лагранжа. Так, для решения задачи

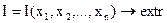(2.25)

при условиях

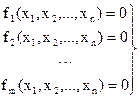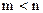, (2.26)

при выполнении условия 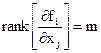нормальная функция Лагранжа имеет вид

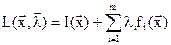. (2.27)

Для определения условного экстремума составляем систему уравнений

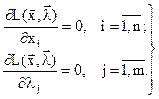(2.28)

Из (m+n) уравнений (2.28) определяем n переменных 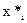, 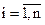и m множителей λ_j, .

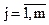Если условия (2.26) таковы, что не выполняется условие регулярности (2.12), то правило множителей с нормальной функцией Лагранжа в этом случае не справедливо. Для перехода к задаче на безусловный экстремум составляют функцию Лагранжа вида

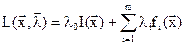, (2.29)

где 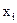, 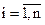– неопределённые множители Лагранжа, и решают задачу таким же образом, как и при составлении нормальной функции Лагранжа.

Следует особо отметить, что метод множителей Лагранжа позволяет найти лишь необходимые условия существования условного экстремума для конкретных функций, имеющих к тому же непрерывные производные. Полученные значения 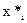, , 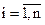могут и не давать экстремального значения функции , что точно так же как и в задачах на безусловный экстремум, рассмотренный выше. Поэтому найденный при решении системы уравнений (2.28) значение переменных 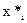, , 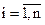должны быть проверенны на экстремум с помощью анализа производных более высокого порядка или какими либо другими методами.

Часто в примерах оптимальных задач анализ условного экстремума требует довольно сложных выкладок при исследовании высших производных. Поэтому по возможности характер найденного экстремума определяется исходя из физического смысла решаемой задачи.

Date: 2015-05-23; view: 709; Нарушение авторских прав