Метод золотого сечения

В геометрии золотым сечением называется такое деление отрезка на две неравные части, при котором отношение всего отрезка к большей части равнялось отношению большей части к меньшей. Первым человеком, который делил линейный отрезок подобным образом, был Евклид. Благодаря многочисленным удивительным свойствам этого соотношения ученые эпохи Возрождения предавали ему почти мистическое значение. Кеплер, например, ставил его рядом с теоремой Пифагора. Освященное веками прославленное золотое сечение в настоящее время нашло эффективное применение в задачах оптимизации.

Метод, разработанный американскими специалистами Кифером и Джонсоном, применим для класса унимодальных функций.

Пусть максимум критерия I(x) находится в интервале [a, b] оси x (внутри или на его краях). По принципу золотого сечения количество пробных точек принимается равным двум, причем они должны размещаться на одинаковых расстояниях от середины интервала таким образом, чтобы отношение длины исключаемого подынтервала к величине интервала поиска оставалось постоянным. При этом на двух следующих друг за другом шагах всегда будет иметь место отношение

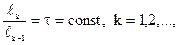
где l_k – длина интервала неопределенности после k-го шага поиска.

Отсюда с учетом l_k-1= l_k + l_k+1 находим

t² + t – 1= 0.

Положительный корень этого уравнения (отрицательный не имеет смысла) равен

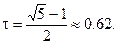
Таким образом, в соответствии с рассматриваемым методом пробные точки x ₁ и x₂ на оси x располагаются следующим образом

x₁ = a + (1 – t)´(b – a);

x₂ = a + t ´(b – a).

В результате анализа двух значений I(x₁) и I(x₂) целевой функции I(x) исключатся один из подинтервалов, где оптимума заведомо быть не может, и выбирается новый интервал неопределенности, который должен исследоваться в дальнейшем. Этот интервал будет состоять из двух неравных отрезков, являющихся отрезками золотого сечения, и содержать одну из предыдущих точек. Симметрично ей выбирают вторую точку внутри нового интервала изложенным выше способом и вычисляют значение функции I(x) в новой точке. Путем анализа двух значений функции I(x) (одно из них получено в предыдущем шаге поиска) определяют новый интервал неопределенности и т. д.

Поиск оптимума завершается, если после k -го шага длина интервала неопределенности станет меньше или равна d, т. е. l_k £ d, где d – заданная погрешность определения оптимума.

Такая стратегия поиска оптимума позволяет сужать интервал неопределенности, каждый раз вычисляя лишь одно значение I(x), а не два, как в методе дихотомии.

Длина интервала неопределенности после k испытаний критерия I(x) равна

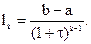
При k=20 (20 измерений показателя качества) 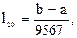что почти в 10 раз меньше длины интервала неопределенности при поиске максимума методом дихотомии.

Date: 2015-05-23; view: 630; Нарушение авторских прав