Метод квадратичной интерполяции

Этот метод может непосредственно применяться к унимодальным функциям одной переменной. Он может быть очень полезным для поиска частного оптимума по отдельным направлениям при решении задач многомерной оптимизации.

В предыдущих двух методах была сделана попытка найти малый интервал, в котором находятся оптимум функции I(x). В рассматриваемом методе применяется иной подход. Он заключается в построении аппроксимирующей модели оптимизируемой функции I(x). Функция I(y) может быть аппроксимирована полиномом второго порядка

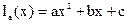(1.5)

по крайней мере, в небольшой области значений, в том числе в области оптимума. При этом положение экстремума I(x) определяется положением экстремума полинома (1.5), поскольку последний вычислить проще.

Экстремум функции I_a(x), как известно, расположен в точке

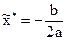. (1.6)

Положим, что окрестность некоторой исходной точки x=x₁ на области определения I(x) аппроксимирована полиномом (1.5). Задача поиска заключается в определении смещения

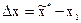, (1.7)

которое приводит из исходного состояния x=x₁ в экстремальное x=x*. Если I(x) строго квадратичная функция, то смещение Dx после первого шага сразу приведет к x*. В противном случае достижение x*требует выполнения итерационной процедуры.

Для определения смещения Dx нужно определить коэффициенты параболы (4.5). Эта задача легко решается, если известны значения I(x) в трех точках. Пусть вычисление I(x) производилось в районе исходного состояния x=x₁ в точках x₁, x₀=x₁ -h, x₂=x₁+h и при этом получено три значения этой функции:

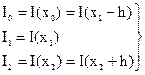, (1.8)

где h – полуинтервал интерполяции, малая постоянная положительная величина.

Подставляя эти значения в уравнение (1.5), получаем систему из трех линейных уравнений с тремя неизвестными a, b и с:

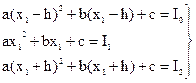. (1.9)

Для того, чтобы эта система имела решение, необходимо, чтобы ее определитель не был равен нулю, то есть

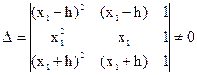. (1.10)

Раскрывая этот определитель, находим

,

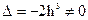что всегда выполняется, поскольку h¹0.

Разрешая систему уравнений (1.9), получаем интересующие нас значения параметров a, b, c и, подставляя их в формулу (1.6), находим положение экстремума параболы

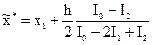. (1.11)

Величина рабочего смещения Dx равна

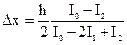. (1.12)

Зная коэффициенты a, b, с можно определить и экстремальное значение функции (1.5) по формуле

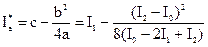, (1.13)

которое является оценкой экстремума критерия I(x).

После выполнения рабочего шага Dx следует проверить, действительно ли найден экстремум. Для этого достаточно вычислить значение функции цели I(x) в предполагаемом экстремуме 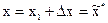и сопоставить его с оценкой (1.13). Если эти величины отличаются не более чем на e, то есть

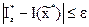, (1.11)

где e – заданная погрешность определения экстремума, то задачу отыскания экстремума можно считать выполненной. При этом x*=x₁+Δx.

Если же условие (1.11) не соблюдается, то это означает, что исходное предположение о квадратичности целевой функции не выполняется и следует продолжать процесс поиска, то есть выполнить следующий цикл, но построение модели производить в окрестности точки x*=x₁. Эта процедура повторяется до тех пор, пока не выполнится условие (1.11).

Вполне очевидно, что критерием окончания процесса поиска экстремума может служить выполнение условия

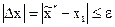. (1.15)

Таким образом, с помощью итерационной процедуры значение x^* уточняется до получения его с заданной погрешностью e.

1 Методы одномерной оптимизации на основе преобразования задач

Многие инженерные задачи связаны с оптимизацией при наличии различного вида ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой проводится поиск оптимума. Однако, несмотря на это, процесс оптимизации становится более сложным, поскольку известные критерии оптимальности решения задачи безусловной оптимизации нельзя использовать при наличии ограничений. При этом может нарушаться даже основное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым градиентом. Часто оптимум достигается в точке, не являющейся стационарной точкой функции . Указанные трудности наталкивают на мысль использовать безусловную оптимизацию вспомогательных функций, составленных с учётом ограничений, для отыскания точки условного оптимума.

Идея преобразования задачи с ограничениями в последовательность задач без ограничений представляется эффективной в связи с наличием надёжных методов безусловной оптимизации. Это позволяет отыскать условный оптимум с приемлемой точностью путём решения относительно небольшого числа не слишком сложных задач.

Ниже рассматривается задача нелинейного программирования следующего вида:

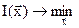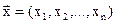, , (2.1)

при ограничениях

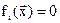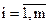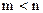, , ; (2.2)

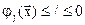, . (2.3)

Начнём рассмотрение с краткого обсуждения метода классического анализа поиска экстремума функции многих переменных без ограничений. Этот метод часто является неотъемлемой частью методов решения преобразованной задачи оптимизации.

Date: 2015-05-23; view: 1927; Нарушение авторских прав