Метод множителей Лагранжа с ограничениями в виде неравенств

Ограничение в виден неравенств существенно усложняет решение задачи оптимизации, несмотря на то что они уменьшают область допустимого изменение переменных. Экстремум функции может достигать не только внутри области, но и на границе области.

Необходимые условия области существования экстремума существования многих переменных с ограничениями в виде неравенств сформулированы в теории Куна-Таккера.

Рассмотрим задачу оптимизации.

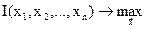(2.36)

при условиях

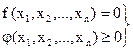. (2.37)

Составим функцию Лагранжа

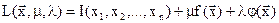(2.38)

где λ и μ – неопределённые множители Лагранжа.

В теореме Куна-Теккера утверждается:

Чтобы точка 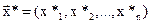являлась экстремумом функции при ограничениях вида (2.37), необходимо, чтобы она была экстремумом функции 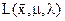и, кроме того, чтобы выполнялось так называемое условие дополняющей нежесткости

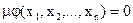(2.39)

Условие дополняющей нежесткости (2.39) означает, что либо неопределённый множитель μ, либо функция φ(х) должны быть равны нулю. В первом случае (если μ = 0) экстремум находится внутри области, ограниченной кривой φ(х) ≥ 0, и поэтому при решении задачи это ограничение не принимается во внимание. Во втором случае (если φ(х) = 0) решение находится на границе, поэтому ограничение в виде неравенства заменяется ограничение в виде равенства и задача решается как обычно методом неопределённых множителей Лагранжа.

Если имеется несколько ограничений в виде неравенств, то каждому из этих ограничений соответствует свой множитель Лагранжа и условие дополнительной нежесткости.

Так, для решения задачи

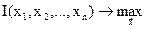(2.40)

При условии

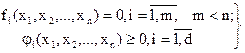(2.41)

функция Лагранжа имеет вид

. ﴾2.42﴿

Условия дополняющие нежесткости тогда будут иметь вид

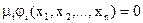﴾2.43﴿

Необходимые условия экстремума:

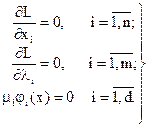(2.44)

Решая системы (2.44), находим оптимальное решение задачи.

Наметим план решения задачи:

1. Сачала задаёмся μ_і = 0, i =1,d, решаем систему (2.44), определяем .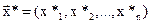

2. Проверяем выполнение неравенств (2.41). Если они выполняются, то найденное 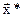является решением задачи.

3.Если какое-либо j – ое неравенство (или несколько неравенств) не выполняется, тогда принимаем μ ≠ 0, а φ_j﴾x﴿=0, решаем задачу с дополнительным условием φ_j﴾x﴿=0 методом множителей Лагранжа и пункты 1-3 повторяем. Эту процедуру повторяем до получения решения задачи.

Date: 2015-05-23; view: 2757; Нарушение авторских прав