Методы измерения сопротивления

Для определения сопротивлений проводников существуют различные методы. Одним из распространенных методов является измерение сопротивлений с помощью вольтметра и амперметра. В этом методе сопротивление проводника определяют по закону Ома для участка цепи :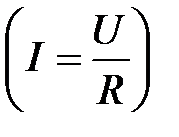

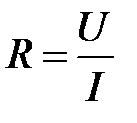, (6.3)

где U – разность потенциалов на концах проводника,

I – сила тока в проводнике.

Сила тока измеряется амперметром, который присоединяется последовательно с неизвестным сопротивлением R_x, а разность потенциалов – вольтметром V, включенным параллельно измеряемому сопротивлению (рисунок 6.1).

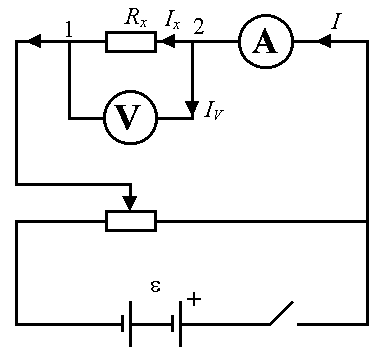
Рисунок 6.1 – Схема для определения сопротивления,
если R_V >> R_x

При включении вольтметра в цепь часть тока протекает через вольтметр, и амперметр покажет не ток, протекающий через сопротивление R_x, а сумму токов, протекающих через R_x и вольтметр V, т.е.

.

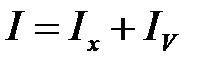Вследствие этого в формулу (6.3) следует подставить не R_x, а общее сопротивление параллельно соединенных ветвей между точками 1 и 2: вольтметра R_V и сопротивления R_x. Это сопротивление равно:

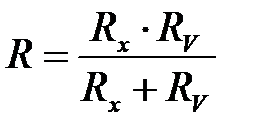. (6.4)

Из формулы (10.4) видно, что 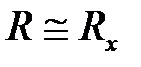, если R_V >> R_x (сопротивление R_V вольтметра должно быть значительно больше измеряемого сопротивления R_x).

Если это условие не выполняется, то неизвестное сопротивление определяется из соотношения (10.4):

.

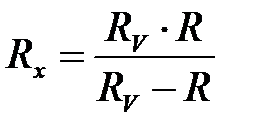Так как 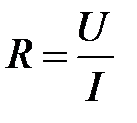, то

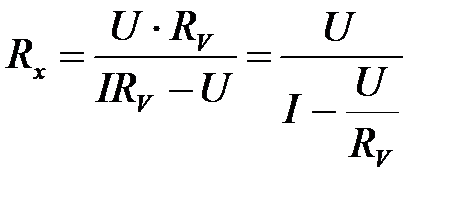. (6.5)

Как следует из формулы (6.5), для определения сопротивления R_x кроме тока I и напряжения U необходимо знать также и сопротивление вольтметра R_V. На некоторых типах вольтметров это сопротивление указано. На многопредельных вольтметрах указывается максимальный ток I _max, протекающий через прибор при отклонении стрелки на всю шкалу. Эта величина является характерной для данного прибора и не зависит от предела измерений. Сопротивление такого прибора находится как отношение:

,

где U ₀ – выбранный предел измерения напряжения. На различных пределах измерения сопротивление R_V различно.

Чтобы исключить влияние вольтметра, амперметр А можно включить так, как показано на рисунке 6.2. В этом случае амперметр измеряет ток, протекающий по неизвестному сопротивлению R_x, но тогда вольтметр показывает разность потенциалов не на R_x, а сумму разностей потенциалов на R_x и на амперметре А. В этом случае отношение 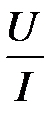дает не величину R_x, а общее сопротивление R между точками 1 и 2 схемы, т.е. R = R_x + R_A (R_A – сопротивление амперметра).

Если R_A << R_x, то общее сопротивление 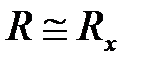. Отношение 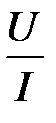даёт величину R_x тем точнее, чем сопротивление амперметра R_A меньше измеряемого. В общем случае, когда о величине неизвестного сопротивления сказать ничего нельзя, расчет ведется по формуле:

.

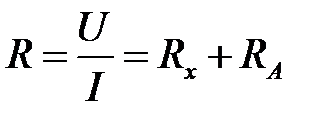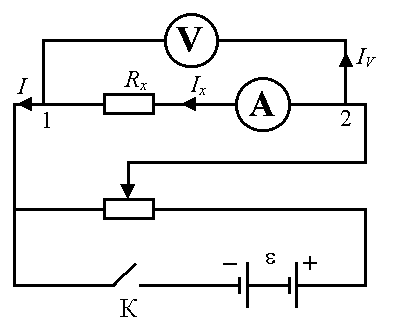
Рисунок 6.2 – Схема для определения сопротивления,

если 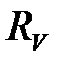сравнима с .

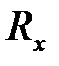Отсюда

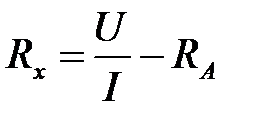. (6.6)

Обычно на амперметре указано или непосредственно его сопротивление R_A или (если прибор многопредельный) величина разности потенциалов U _max между зажимами прибора, соответствующая отклонению стрелки на всю шкалу. В последнем случае сопротивление прибора равно:

,

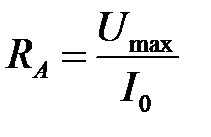где I ₀ – выбранный предел измерения тока.

На амперметрах с наружными шунтами также бывает указана величина U _max, при делении которой на величину тока, указанного на шунте, получается сопротивление прибора вместе с шунтом.

На практике иногда не учитывают сопротивлений приборов, т.е. отношение 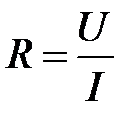принимают за величину неизвестного сопротивления. Систематическая ошибка, которая возникает при этом, зависит от величины измеряемого сопротивления и от сопротивлений применяемых приборов.

Как следует из рассуждений, схемы на рисунках 6.1 и 6.2 неравноценны: при одинаковых приборах схема 6.1 даёт меньшую ошибку при малом неизвестном сопротивлении, схема 6.2 – при большом. Если ошибка незначительна при измерениях токов и разностей потенциалов, то нет надобности учитывать влияние сопротивлений приборов и с достаточной степенью точности можно принять:

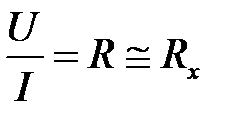. (6.7)

Очень точным и весьма часто применяемым в лабораторной практике методом является метод мостика постоянного тока (мост Уитстона.).

Принципиальная схема мостика приведена на рисунке 6.3. Измеряемое сопротивление R_x и три других переменных сопротивления R ₀, R ₁ и R ₂ соединяются так, что образуется замкнутый четырехугольник АВСD. В одну диагональ четырехугольника включён гальванометр (этот участок и является мостиком), а в другую через ключ К – источник постоянного тока e. При замыкании ключей К и К₁ гальванометр показывает наличие тока I_g в цепи ДС, но можно подобрать такие сопротивления R ₁ и R ₂, что потенциалы точек С и Д станут равными, тогда ток в цепи гальванометра будет отсутствовать – мост уравновешен (при замыкания ключа К₁ стрелка гальванометра остается на нуле).

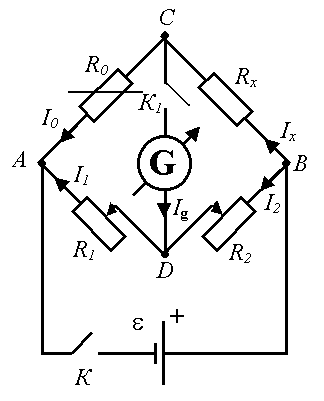
Рисунок 6.3 – Мост Уитстона

В этом случае имеют место следующие соотношения:

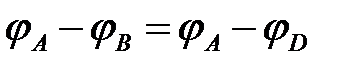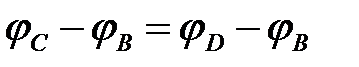, , (6.8)

т.е.

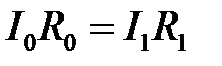(6.9)

и

. (6.10)

Применяя к узлам С и D первое правило Кирхгофа, в случае отсутствия тока через гальванометр будем иметь:

, .

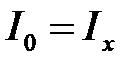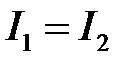Деля уравнение (10.9) на уравнение (6.10) и произведя сокращение, получим:

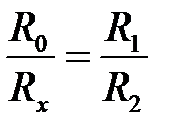. (6.11)

Откуда искомое сопротивление R_x равно:

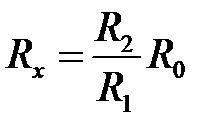. (6.12)

Соотношение (10.12) можно получить, используя правила Кирхгофа:

1. Первое правило Кирхгофа – алгебраическая сумма токов, сходящихся в узле, равна нулю: 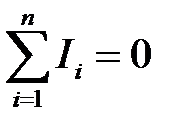. Узлом называется точка, в которой сходится более, чем два проводника. Направления токов через элементы цепи выбираются произвольным образом. Ток, текущий к узлу, считается имеющим один знак (например, плюс), текущий от узла – имеющим другой знак (например, минус). Уравнения первого правила Кирхгофа можно написать для каждого из N узлов цепи, но независимыми будет только N-1 уравнение.

2. Второе правило Кирхгофа применяется для замкнутого контура электрической цепи – алгебраическая сумма произведения токов на сопротивления соответствующих участков контура равна алгебраической сумме ЭДС, встречающихся в контуре: 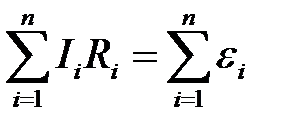. Для выбранного контура выбирается произвольным образом направление обхода и ток на данном участке считается положительным, если его направление совпадает с направлением обхода контура. ЭДС считается положительной, если при данном направлении обхода мы переходим внутри источника тока от отрицательного полюса источника к положительному.

Для данной электрической схемы всего должно быть составлено 6 уравнений (число уравнений определяется числом неизвестных токов). По первому правилу Кирхгофа можно составить три уравнения (4 узла) и три уравнения по второму правилу Кирхгофа,

Применим первое правило Кирхгофа к узлам С и D. Будем считать, что при замкнутом ключе К ток через гальванометр I_g направлен от точки С к точке D. Тогда имеем:

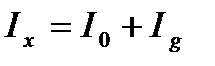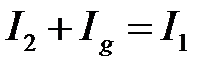, . (6.13)

По второму правилу Кирхгофа для контуров САDС и ВСDВ (обход против часовой стрелки) получим:

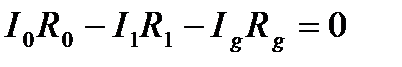, . (6.14)

При равновесии мостика Уитстона I_g = 0 и соотношения (6.13) и (6.14) примут вид:

, ,

, ,

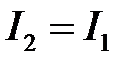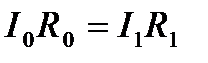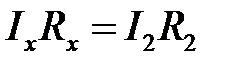откуда .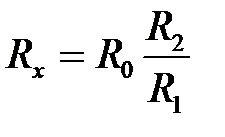

Метод измерения сопротивлений с помощью моста Уитстона является методом сравнения или нулевым методом, так как в этом случае производится непосредственное сравнение сопротивлений, а гальванометр используется в качестве индикатора отсутствия тока (нуль-гальванометр). Поэтому точность измерения определяется только точностью магазинов сопротивлений и чувствительностью гальванометра.

Date: 2015-05-22; view: 1059; Нарушение авторских прав