Определенный интеграл

Пример 7. Найти площадь фигуры, ограниченной параболой 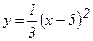и прямой у = х + 1.

Решение.

Площадь фигуры, ограниченной сверху непрерывной кривой у = f(x), снизу – непрерывной кривой у = φ(х), слева – прямой х = а, справа – прямой х = в, вычисляется по формуле

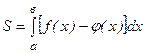(7)

Определенный интеграл вычисляется по формуле Ньютона – Лейбница:

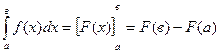, (8)

для которого необходимо найти первообразную функцию F(x) и вместо переменной х подставить сначала верхний предел в, затем нижний предел а и из 1-го результата вычесть второй.

Определим точки пересечения данных линий, решив совместно систему уравнений

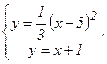
Подставив в 1-ое уравнение системы суммы (х + 1), вместо у, получим:

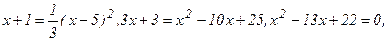
откуда х₁ = 2, х₂ = 11 и, следовательно, у₁=3, у₂=12. Таким образом, парабола и прямая пересекаются в точках А(2; 3) и В(11; 12) (рис. 10).

Так как сверху фигура ограниченна прямой, а снизу – параболой, то применяя формулу (7), имеем:

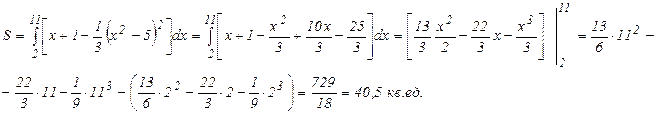
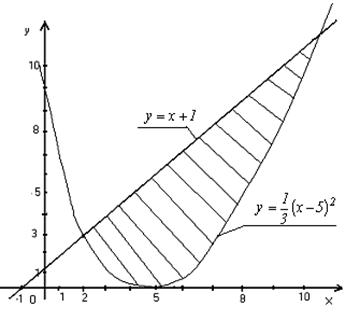
Рис. 10

Дифференциальные уравнения (ДУ)

ДУ І порядка имеет вид:

F = (x, y, y^/) (1)

или (если его можно разрешить относительно у^/) вид:

у^/ = f (x, y) (2)

Решение уравнения (1) или (2), содержащее произвольную постоянную С, то есть имеющее вид у = φ (х, С), называется общим решением этого уравнения. Если это решение получается в неявной форме Ф (х, у, С) = 0, то его называют общим интегралом уравнения (1) или (2).

Если придать произвольной постоянной С некоторое фиксированное значение, то из общего решения (общего интеграла) получим частное решение (частный интеграл) этого уравнения.

Уравнение І порядка Р (х, у) dx + Q (x, y) dy = 0 называется уравнением с разделяющимися переменными, если функция Р (х, у) и Q (х, у) разлагаются на множители, зависящие каждый только от данной переменной:

f₁ (x) f₂ (y) dx + φ₁ (x) φ₂ (y) dy = 0 (3)

В этом уравнении путем деления его членов на f₂ (y)φ₁ (x) переменные разделяются и общий интеграл находится почленным интегрированием:

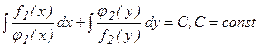
Функция f(x, y) называется однородной измерения m, если f (λ x, λy) = λ^m f(x, y).

Однородное ДУ первого порядка называется уравнение у^/ = f (х,у), если f(х,у) – однородная функция нулевого измерения.

Замечаение. Уравнение вида P(x,y)dx + Q(x,y)dy = 0 будет однородным, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.

Однородное уравнение может быть приведено к виду у^/ = f(y/x). С помощью подстановки у/х = t однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции t = t(x).

Уравнение вида:

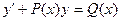(4)

где Р (х) и Q (x) – заданные непрерывные функции, называются линейным. ДУ І порядка (у и у^/ входят в первых степенях, не перемножаясь между собой). Если Q (x) ≠ 0, то уравнение называется линейным неоднородным, а если Q = 0 – линейным однородным в смысле правой части.

Неоднородное линейное ДУ І порядка посредством замены искомой функции у = и σ сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.

Пример 1. Найти общее решение ДУ.

а)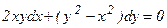

б)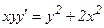

Решение.

а) Данное уравнение является однородным, так как функции Р(х, у)=2ху и Q(х, у)=(у²-х²) – однородные второго измерения относительно х, у:

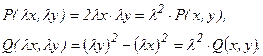
Применяем подстановку у = хt, где t – некратная функция аргумента х.

Если у = хt, то дифференциал dy = tdx + xdt, и данное уравнение примет вид:

2х ^. xtdx + (x²t² – x²) (tdx + xdt) = 0

Сократив на х², будем иметь:

Получилось уравнение с разделенными переменными относительно х и t. Интегрируя, найдем общее решение этого уравнения:

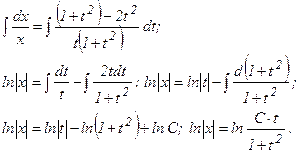
Потенцируя, находим 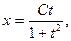или х (1 + t²) = Сt. Из введенной подстановки следует, что 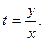Следовательно, 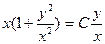или х² + у²= Су – общее решение данного уравнения.

б) Поделим обе части уравнения на произведение функции ху, получим:

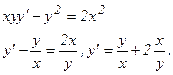
Введем подстановку 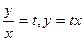, откуда 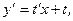где 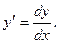Тогда последнее уравнение примет вид: 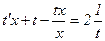или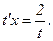

Разделяя переменные и интегрируя, имеем:

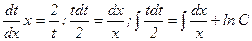
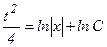или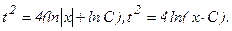

Возвращаясь к переменным х и у, получаем 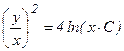или 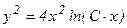- искомое общее решение ДУ.

Пример 2. Решить уравнение.

а)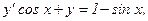

б)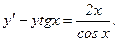

Решение.

а) Поделим обе части уравнения на соs х:

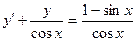(1)

Это линейное неоднородное уравнение. Введем подстановку у = иσ, тогда у΄= и΄σ + иσ΄ и данное уравнение (1) преобразуется к виду

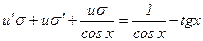или

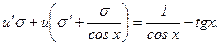
Так как искомая функция у представлена в виде произведения двух вспомогательных функций и и σ, то одну из них можно выбрать произвольно. Выберем в качестве σ какой-либо частный интеграл уравнения:

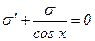(2)

Тогда для отыскивания функции и получим уравнение:

(3)

Уравнение (2), есть уравнение с разделяющимися переменными относительно σ и х. Решим его:

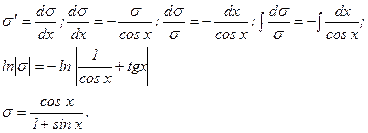
Чтобы равенство (2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрирования находим то частное решение, которое соответствует значению произвольной постоянной С=0.

Подставив в (3) найденное выражение для σ, получим:

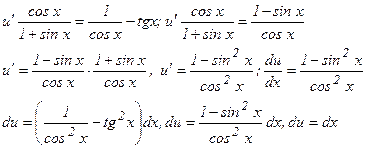
Интегрируя, получаем:

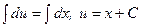
Тогда

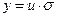или

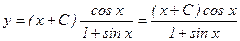- общее решение уравнения (1).

б) Данное уравнение является линейным, так как оно содержит искомую функцию у и ее производную у^/ в первой степени и не содержит их произведений.

Применяем подстановку 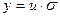, тогда 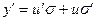и уравнение примет вид:

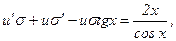или

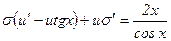(4)

Полагаем

u΄-utg x = 0 (5)

Тогда уравнение (4) примет вид:

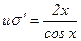(6)

Уравнение (5) – уравнение с разделяющимися переменными. Решим его:

(значение произвольной постоянной принимаем С =0)

Подставив в (6) найденное выражение для и, получим:

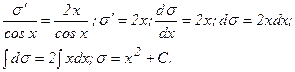
Тогда 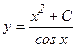- общее решение данного уравнения.

Дифференциальным уравнением n -го порядка называется уравнение вида:

F(x, y΄y΄΄,…y⁽ⁿ⁾) = 0

Решением такого уравнения служит всякая n раз дифференцированная функция у = φ (х), которая обращает данное уравнение в тождество, т.е.:

F (x, φ(x), φ΄(x), φ⁽ⁿ⁾(x)) = 0.

Для дифференцированного уравнения вида

F (x, y^(k), y^(k+1), …, y⁽ⁿ⁾)= 0,

Не содержащего искомой функции у, порядок уравнения можно понизить, взяв за новую неизвестную функцию низшую из производных данного уравнения, т.е. пологая y^(k)=z.

Тогда получим уравнение

F (x, z, z΄, …, z^(n-k)) = 0

Таким образом, порядок уравнения понижается на k единиц.

Пример 3. Найти общее решение уравнения

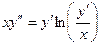(1)

Решение.

Данное уравнение II порядка не содержит явно функцию у. Положим у΄=z, где z – некоторая функция аргумента х. Если у΄=z, то у ΄΄ =z΄ и данное уравнение (1) примет вид: 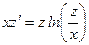или

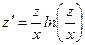(2)

Это однородное уравнение I порядка.

Введем подстановку 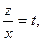откуда z = xt, z΄=t΄x + t и уравнение примет вид:

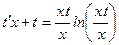или

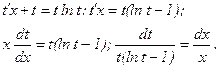
Интегрируя, находим:

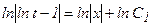, или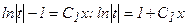

Потенцируя, получаем:

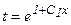или 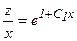откуда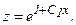

Возвращаясь к переменной у, приходим к уравнению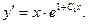

Это уравнение вида у⁽ⁿ⁾=f(x), решение которого находится n – кратным интегрированием.

Следовательно, 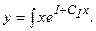Для нахождения данного интеграла применяем формулу интегрирования по частям:

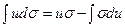(3)

Положим u = x, dσ= 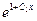dx, тогда du = dx, 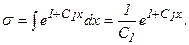Применяя формулу (3), получаем общее решение уравнения (1):

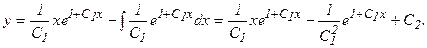
Для ДУ вида

F (y, y΄, y΄΄, …, y⁽ⁿ⁾) = 0,

не содержащего независимой переменной х, допускается понижение порядка на единицу, если положить у^/ = z, а за новый аргумент принять сам у. В этом случае у΄΄, у΄΄΄, … выразятся по формулам (они выводятся по правилу дифференцирования сложной функции:

… через z и производные от z по y, причем порядок уравнения понизится на единицу.

Пример 4. Решить уравнение у΄΄(1 + у) = у΄²+ у΄.

Решение.

Уравнение не содержит независимой переменной х. Положим у΄= z, y΄΄= 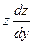и данное уравнение примет вид: 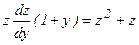или 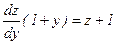; это уравнение первого порядка относительно z c разделяющимися переменными. Разделяем переменные и интегрируем:

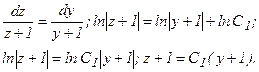
Возвращаясь к переменной у, получаем уравнение у΄=С₁(у + 1 ) – 1; это уравнение I порядка с разделяющимися переменными.

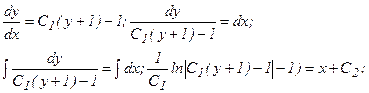
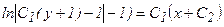– общий интеграл данного уравнения.

Линейные неоднородные дифференциальные уравнения II порядка с постоянными коэффициентами.

Уравнение 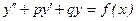, (1)

где p и q – действительные числа, f(x) – известная непрерывная функция, называется линейным неоднородным дифференциальным уравнением II порядка с постоянным коэффициентом.

Функция y=φ(x, C₁, C₂), удовлетворяющая уравнению (1) при любых значениях произвольных С₁ и С₂, называется его общим решением.

Решение уравнения (1), получающиеся из общего решения при конкретных значениях постоянных С₁ и С₂, называется частным решением уравнения (1).

Т.к. в функцию y=φ(x, C₁, C₂) входят две произвольные постоянные C₁ и C₂; то для выделения из общего решения уравнения (1) некоторого частного решения необходимо иметь два начальных условия: если х=х₀, то у=у₀, у′= у′₀, то есть у(х₀)=у₀, у′(х₀)= у′₀..

Для общего решения неоднородного уравнения (1) справедлива следующая теорема.

ТЕОРЕМА. Общее решение у_об.н. неоднородное уравнение (1) равно сумме общего решения у_одн соответствующего однородного уравнения 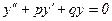и любого частного решения у_ч.н. данного неоднородного уравнения (1).

у_об.н.=у_одн+у_ч.н.

Согласно этой теореме для решения уравнения (1) вначале находится функция у_одн – решение однородного дифференциального уравнения

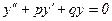, (2)

где p, q – постоянные действительные числа.

Общее решение уравнения (2) находится с помощью характеристического уравнения.

k²+pk+q=0, (3)

которое получается из уравнения (2), если, сохраняя в нем коэффициенты p и q, заменить функцию у′ единицей, а все ее производные соответствующими степенями k.

При этом:

1) Если корни k₁ и k₂ характеристического уравнения (3) действительные и различные, то общее решение уравнения (2) выражается формулой

.

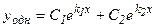2) Если корни k₁ и k₂ характеристического уравнения (3) действительные и равные (k₁=k₂), то общее решение уравнения (2) выражается формулой

.

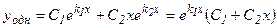3) Если корни k₁ и k₂ характеристического уравнения (3) комплексные (k₁=α+βi, k₂= α-βi), то общее решение уравнения(2) есть:

.

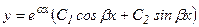Для некоторых специальных видов функции f(x) частное решение у_ч.н. уравнение (1) можно найти методом неопределенных коэффициентов. По виду правой части f(x) можно заранее указать вид частного решения у_{ч.н .}, где неизвестны лишь числовые коэффициенты, в следующих простейших случаях.

I. f(x)=P_n(x), где P_n(x) – многочлен степени n.

В этом случае у_ч.н. есть многочлен Q_n(x) той же самой степени n,что и многочлен P_n(x), если число 0 не является корнем характеристического уравнения (3); если же число 0 является корнем характеристического уравнения кратности r, то у_ч.н.=х^кQ_n(x).

II. f(x)=ae^mx (a, m – некоторые числа).

В этом случае у_ч.н.=Ае^mx, если число m не является корнем характеристического уравнения (3) и у_ч.н.=Аx^rе^mx, если число m является корнем характеристического уравнения кратности r.

Здесь А – подлежащий определению коэффициент.

III. f(x)=e^mx P_n(x), где P_n(x) – многочлен степени n.

В этом случае у_ч.н.=е^mxQ_n(x), если число m не является корнем характеристического уравнения и у_ч.н.=х^rе^mxQ_n(x), если число m является корнем характеристического уравнения кратности r. Здесь Q_n(x) – многочлен той же степени n, что и P_n(x).

Например: Q₀(x)=А;

Q₁(x)=Ах+В;

Q₂(x)=Ах²+Вх+С;

Q₃(x)=Ах³+Вх²+Сх+D; и т.д.

Коэффициенты А,В,С,D подлежат определению.

IV. f(x)=e^αx(acosβx+bsinβx). Тогда у_ч.н.=е^αx(Аcosβx+Вsinβx), если число α±βi не является корнем характеристического уравнения и у_ч.н.=хе^αx(Аcosβx+Вsinβ x), если число α±βi является корнем характеристического уравнения.

Здесь А и В - подлежащие определению коэффициенты.

V. Правая часть уравнения (1) функция f(x) есть сумма указанных функций.

Тогда частное решение у_ч.н. этого уравнения есть сумма частных решений уравнений с той же левой частью, что и уравнение (1), а правые части этих уравнений есть каждое слагаемое правой части уравнения (1).

Пример 5. Найти частное решение дифференциального уравнения 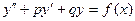, удовлетворяющее начальным условиям у(0)=у₀, у′(0)=у′₀.

а) y″-2y′+10y=6cos2x+4sin2х, y(0)=1,y′(0)=6;

б) y″-9y′8y=3x²+2x+1, y(0)=

Решение: а) Вначале находим общее решение однородного уравнения y″-2y′+10y=0; соответствующего данному неоднородному уравнению. Составим и решим его характеристическое уравнение.

k²-2k+10=0

D=4-4·1·10=-36<0, значит, уравнение имеет два комплексно-сопряженных числа.

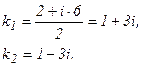
Тогда общее решение соответствующего однородного уравнения будет (согласно п.3).

у_одн=e^x(C₁cos3x+C₂sin3x).

Правая часть данного уравнения f(x)=6cos 2x+4sin2x, где по п. IV α=0, a=6, b=4, β=2 и числа α±βi =±2i не является корнем характеристического уравнения.

Тогда частное решение данного неоднородного уравнения будет функция вида

у_ч.н.=е^0x(Аcos 2x+Вsin2x)= Аcos 2x+Вsin2x.

Найдем производные первого и второго порядка функции у_ч.н.:

y′_ч.н.=-2Asin2x+2Bcos2x,

y″_ч.н=-4Acos2x-4Bsin2x.

Представим у_ч.н, y′_ч.н, y″_ч.н в данное неоднородное уравнение:

-4Acos2x-4Bsin2x-2(_.-2Asin2x+2Bcos2x)+10(Аcos 2x+Вsin2x)= 6cos2x+4sin2x,

(6А-4В)cos 2x+(6B+4A)sin2x=6cos 2x+4sin2x, которое будет тождеством только при равенстве коэффициентов у подобных членов в обеих его частях:

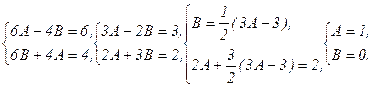
Следовательно, у_ч.н=cos 2x и общее решение данного неоднородного уравнения будет:

у_об.н.=у_одн+у_ч.н.,

у_об.н= e^x(C₁cos3x+C₂sin3x)+ cos 2x

Используя начальные условия, найдем значения произвольных постоянных С₁ и С₂. Подставляя в общее решение заданные значения х =0, у =1 (первое начальное условие), получим 1= e⁰(C₁cos0+C₂sin0)+ cos 0 или 1=С₁+1, С₁=0.

Дифференцируем общее решение:

у′= e^x(C₁cos3x+C₂sin3x)+ e^x(-3C₁sin3x+3C₂ cos3x)-2sin2x или

у′= e^x((C₁+3C₂ )cos3x+(C₂-3C₁)sin3x)-2sin2x

Подставим в результат дифференцирования заданные значения х =0 и у′ =6 (второе начальное условие), получим второе уравнение с неизвестными С₁ и С₂:

6= e⁰((C₁+3C₂ )cos0+(C₂-3C₁)sin0)-2sin2x или С₁+3С₂=6.

Решая полученные уравнения как систему, найдем С₁ =0 и С₂ =2. Подставляя значения С₁ =0, С₂ =2 в общее решение, получим искомое частное решение, удовлетворяющее заданным начальным условиям.

у=2е^хsin3x+cos2x.

б) Составим однородное уравнение, соответствующее данному неоднородному

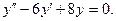
Его характеристическое уравнение k²-6k+8=0 имеет корни k₁=2, k₂=4, поэтому общее решение соответствующего однородного уравнения будет

у_одн=C₁е^2х+С₂е^4х.

Теперь находим частное решение у_ч.н. данного неоднородного уравнения. Для правой части данного уравнения f(x)=3x²+2x+1. Число 0 не является корнем характеристического уравнения, поэтому у_ч.н. есть многочлен той же степени, что и f(x), т.е. многочлен второй степени у_ч.н.=Ах²+Вх+С. Отсюда, дифференцируя, находим у′_ч.н.=2Ах+В, у″_ч.н.=2А и подставляя у_ч.н., у′_ч.н. и у″_ч.н. в данное уравнение, получим равенство

2А-6(2Ах+В)+8(Ах²+Вх+С)=3х²+2х+1,

2А-12Ах+6В+8Ах²+8Вх+8С=3х²+2х+1,

8Ах²+(8В-12А)х+(8С-6В+2А)=3х²+2х+1.

Приравнивая коэффициенты при одинаковых степенях х из обеих его частей, а только при этом условии оно будет тождественным, получим систему:

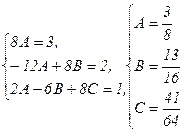
Следовательно, у_ч.н.=С₁е^2х+С₂е^4х+ 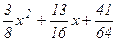или

у_ч.н.=С₁е^2х+С₂е^4х+ 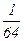(24х²+52х+41).

Используя начальные условия, найдем значения произвольных постоянных С₁ и С₂. Подставляя в общее решение первое начальное условие (х =0, у = ) получим

С₁+С₂+ 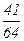= , С₁+С₂=1.

Дифференцируя общее решение

у′=2С₁е^2х+4С₂е^4х+ 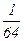(48х+52).

и подставляя в результат второе начальное условие(х =0, у′ = 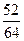) получим второе уравнение с неизвестными С₁ и С₂.

2 С₁+4С₂+ = , 2 С₁+4С₂=0, С₁+2С₂=0.

Решив полученные уравнения как систему, найдем С₁ и С₂:

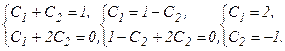
Подставляя значения С₁ =2, С₂ =-1 в общее решение получим искомое частное решение, удовлетворяющее заданным начальным условиям:

у=2е^2х-е^4х+ 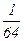(24х²+52х+41).

Линейные однородные системы ДУ с постоянными коэффициентами.

Пусть данная система n- линейных ДУ с n неизвестными функциями, коэффициенты которой постоянные:

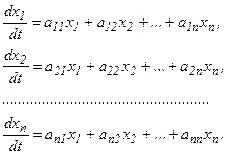
Эту систему можно записать в виде одного матричного уравнения:

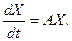
Здесь

Ищем решение системы в виде:

х₁=р₁ е^λt, х₂ = р₂е^λt, …, х_n=p_ne^λt, где λ = const, p_i=const (i = 1, 2, …, n).

Подставив значения х₁, х₂, …, х_n в систему ДУ, получим систему линейных алгебраических уравнений относительно р₁, р₂, …, р_n:

Система должна иметь ненулевое решение, поэтому для определения λ получаем уравнение n -ой степени, которое является характеристическим уравнением системы:

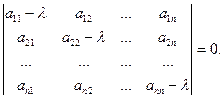
Предположим, что характеристическое уравнение имеет n различных корней λ₁, λ₂, …, λ_n, которые являются характеристическими числами матрицы А.

Каждому характеристическому числу λ_k соответствует свой собственный вектор (р_1k, p_2k, …, p_nk), где k = 1, 2, 3, …, n. Тогда система ДУ имеет n решений.

1-ое решение, соответствующее корню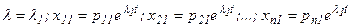

2-ое решение, соответствующее корню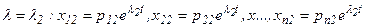

………………………………………………………………………………………………………..

n -ое решение, соответствующее корню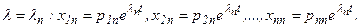

Мы получили фундаментальную систему решений. Общее решение системы таково:

Пример 6. Найти общее решение системы ДУ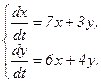

Решение.

Запишем данную систему ДУ в виде матричного уравнения: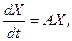

где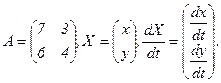

Составим характеристическое уравнение матрицы системы:

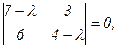или (7 – λ) (4 – λ) - 18 = 0, λ²- 11λ+ 10 = 0.

Корни характеристического уравнения λ₁ = 1, λ₂ = 10 – характеристические числа матрицы.

При λ₁ = 1, уравнение для определения собственного вектора имеет вид 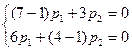и сводится к одному уравнению 2р₁+р₂= 0. последнее определяет вектор с координатами (1; -2).

При λ = 10, получаем уравнение 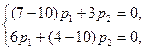или р₁ – р₂= 0. Это уравнение определяет вектор с координатами (1; 1). Получаем фундаментальную систему решения:

для λ = 1: х₁₁ = е^t, х₂₁= -2е^t;

для λ= 10: х₁₂ = е^10t, x₂₂=e^10t.

Общее решение системы имеет вид:

x = C₁x₁₁+C₂x₁₂, x = C₁e^t + C₂e^10t,

y = C₁x₂₁ + C₂x₂₂, y = -2C₁e^t + C₂e^10t.

Кратные, криволинейные и поверхностные интегралы.

Площадь плоской фигуры, ограниченной областью D, находится по формуле:

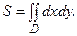
Если область D определена, например, неравенствами а≤x≤b, φ₁(х)≤y≤φ₂(х), то

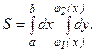
Если область D в полярных координатах определена неравенствами α≤θ≤β, φ(θ)≤ρ≤f(θ), то

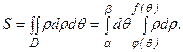
Преобразование прямоугольных координат х, у к полярным координатам ρ, θ, осуществляется по формулам х=ρcosθ, y= ρsinθ, где ρ – полярный радиус – вектор произвольной точки М, θ – полярный угол точки М.

Пример 7. Найти площадь фигуры, ограниченной кривой:

а) (х²+у²)=2а²ху (лемниската)

б) х³+у³=аху (площадь петли).

Решение: а) Полагая х=ρcosθ, y=ρsinθ, преобразуем уравнение кривой к полярным координатам. В результате получим:

(ρ²cos²θ+ ρ²sin²θ)²=2а²ρ²cosθsinθ или ρ²=2а²cosθsinθ=а²sin2θ.

Построим кривую. Разрешив уравнение относительно ρ, находим ρ=±а 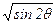. Из того, что в правой части равенства стоит двойной знак «±», а также из того, что ρ(-θ)=±а 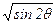, заключаем, что лемниската расположена симметрично относительно начала координат.

Исследуем форму лемнискаты для I четверти, т. е. для случая ρ≥0, 0≤θ≤π∕2. Для этого составим таблицу, учитывая, что ρ=±а :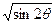

θ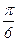
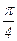
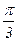
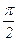
ρ		0,9а	а	0,9а

Построим данную кривую.

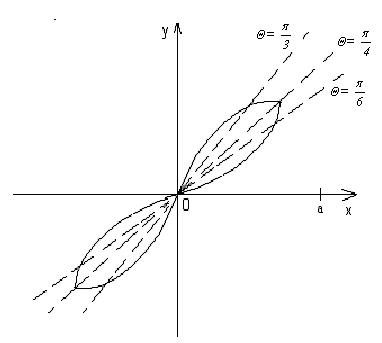
Нетрудно заметить, что θ может измениться только в промежутке от 0 до 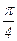, и такому изменению угла θ соответствует четверть искомой площади. Следовательно,

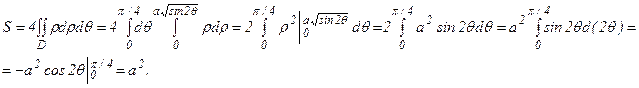
Т.о., площадь искомой фигуры S=a² кв.ед.

б) х³+у³=аху

Преобразуем данное уравнение к полярным координатам

ρ³(sin³θ+cos³θ)=aρsinθcosθ, т.е.

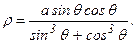
Построим петлю в I четверти, т.е. ρ>0, 0≤θ≤π/2.

Составим таблицу значений.

θ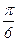
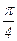
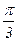
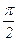
ρ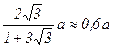

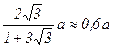
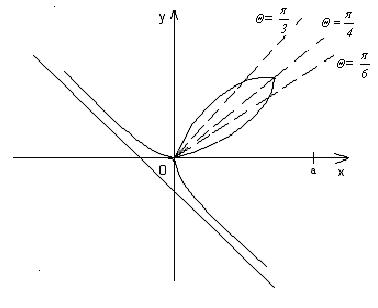
Осью симметрии петли является луч θ= 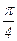, поэтому

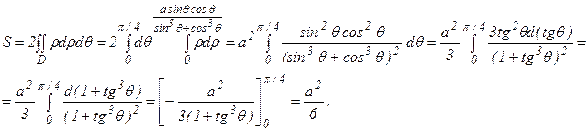
Т.о., площадь петли S= кв.ед.

Date: 2015-04-23; view: 708; Нарушение авторских прав