Уравнение математической физики

Решение уравнения колебания струны методом характеристик (методом Даламбера)

Струной называется тонкая нить, которая может свободно изгибаться. Пусть струна находится под действием сильного начального натяжения Т₀.

Если вывести струну из положения равновесия и подвергнуть действию какой-нибудь силы, то струна начнет колебаться.

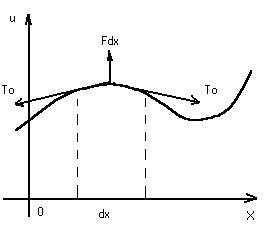
рис. 11

Ограничимся рассмотрением тех колебаний, при которых отклонения точек струны от положения покоя малы, в любой момент времени все точки струны находятся в одной и той же плоскости и каждая точка струны колеблется, оставаясь на одном и том же перпендикуляре к прямой, соответствующем состоянию покоя струны.

Принимая эту прямую за ось Ох, обозначим через и = и(х, t) отклонение точек струны от положения равновесия в момент времени t. При каждом фиксированном значении t график функции и = и(х, t) на плоскости хО и дает форму струны в момент времени t.

Функция и = и(х, t) удовлетворяет дифференцируемому уравнению

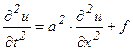(1)

где а²= Т₀ / ς, ƒ= F / ς, ς- масса единицы длины (линейная плотность струны), F – сила, действующая на струну перпендикулярно оси О х и рассчитанная на единицу длины.

Если внешняя сила отсутствует, т.е. f = 0, то получится уравнение свободных колебаний струны.

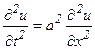(2)

Для полного определения движения струны нужно задать в начальный момент времени t=0 форму и скорость струны, т.е. положение ее точек и их скорость в виде функции абсцисс х этих точек. Пусть

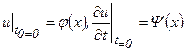(3)

Эти условия (3) называются начальными условиями задачи.

Общее решение дифференциального уравнения (2) свободных колебаний имеет вид:

и = Ф₁ (х – аt) + Ф₂(х + аt)

Подобрав функции Ф₁ и Ф₂ так, чтобы функция и = и (х, t) удовлетворяла приведенным начальным условием, приходим к решению исходного дифференциального уравнения в виде

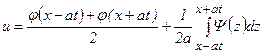(4)

Пример 1. Найти решение и = и (х, t) уравнения 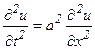методом Даламбера, если в начальный момент времени t= 0 форма струны и скорость точки струны с абсциссой х определяются соответственно функциями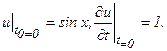

Решение

Здесь φ(х) = sin x, ψ(x) = 1, отсюда по формуле (4) имеем:

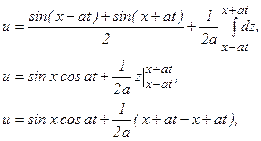
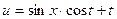- решение уравнения свободных колебаний струны при заданных начальных условиях.

Date: 2015-04-23; view: 631; Нарушение авторских прав