
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Контрольная работа №1
|
|
1 - 10. Даны векторы а (а1; а2; а3), b (b1; b2; b3), с (с1; с2; с3) и d (d1; d2; d3) в некотором базисе. Показать, что векторы а, b, c образуют базис, и найти координаты вектора d в этом базисе.
1. а (1;2;3), b (-1;3;2), с (7;-3;5), d (6;10;17).
2. а (4;7;8), b (9;1;3), с (2;-4;1), d (1;-13;-13).
3. а (8;2;3), b (4;6;10), с (3;-2;1), d (7;4;11).
4. а (10;3;1), b (1;4;2), с (3;9;2), d (19;30;7).
5. а (2;4;1), b (1;3;6), с (5;3;1), d (24;20;6).
6. а (1;7;3), b (3;4;2), с (4;8;5), d (7;32;14).
7. а (1;-2;3), b (4;7;2), с (6;4;2), d (14;18;6).
8. а (1;4;3), b (6;8;5), с (3;1;4), d (21;18;33).
9. а (2;7;3), b (3;1;8), c (2;-7;4), d (16;14;27).
10. а (7;2;1), b (4;3;5), с (3;4;-2), d (2;-5;-13).
11 - 20. Даны координаты вершин пирамиды А1А2А3А4. Найти 1) длину ребра А1А2; 2) угол между ребром А1А2 и А1А4; 3) угол между ребрами А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
11. А1 (4;2;5), А2 (0;7;2), А3 (0;2;7), А4 (1;5;0).
12. А1 (4;4;10), А2 (4;10;2), А3 (2;8;4), А4 (9;6;4).
13. А1 (4;6;5), А2 (6;9;4), А3 (2;10;10), А4 (7;5;9).
14. А1 (3;5;4), А2 (8;7;4), А3 (5;10;4), А4 (4;7;8).
15. А1 (10;6;6), А2 (-2;8;2), А3 (6;8;9), А4 (7;10;3).
16. А1 (1;8;2), А2 (5;2;6), А3 (5;7;4), А4 (4;10;9).
17. А1 (6;6;5), А2 (4;9;5), А3 (4;6;11), А4 (6;9;3).
18. А1 (7;2;2), А2 (5;7;7), А3 (5;3;1), А4 (2;3;7).
19. А1 (8;6;4), А2 (10;5;5), А3 (5;6;8), А4 (8;10;7).
20. А1 (7;7;3), А2 (6;5;8), А3 (3;5;8), А4 (8;4;1).
21. Уравнение одной из сторон квадрата х + 3у – 5 = 0. Составить уравнения трех остальных сторон квадрата, если (-1;0) – точка пересечения его диагоналей.
22. Даны уравнения одной из сторон ромба х - 3у + 10 = 0 и одной из его диагоналей х + 4у – 4 = 0; диагонали ромба пересекаются в точке (0, 1). Найти уравнения остальных сторон ромба.
23. Уравнения двух сторон параллелограмма х + 2у + 2 = 0 и х + у = 0, а уравнение одной из его диагоналей х – 2 = 0. Найти координаты вершин параллелограмма.
24. Даны две вершины А(-3;3) и В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон.
25. Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВСD (AD 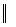 ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
26. Даны уравнения двух сторон треугольника 5х - 4у + 15 = 0 и 4х + у – 9 = 0. Его медианы пересекаются в точке (0;2). Составить уравнение третьей стороны треугольника.
27. Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С.
28. Даны уравнения двух высот треугольника х + у = 4 и у = 2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника.
29. Даны уравнения двух медиан треугольника х - 2у + 1 = 0 и у – 1 = 0 и одна из его вершин (1;3). Составить уравнения его сторон.
30. Две стороны треугольника заданы уравнениями 5х - 2у – 8 = 0 и 3х - 2у – 8 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
31. Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки А(5;0) относятся как 2:1.
32. Составить уравнение линии, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее от прямой х = - 4.
33. Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 5х + 8 = 0 относятся как 5: 4.
34. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
35. Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 2х + 5 = 0 относятся как 4: 5.
36. Составить уравнение линии, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В(26;0).
37. Составить уравнение линии, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у – 4 = 0.
38. Составить уравнение линии, каждая точка которой равноотстоит от оси ординат и от окружности х2 + у2 = 4х.
39. Составить уравнение линии, каждая точка которой равноудалена от точки А(2;6) и о прямой у + 2 = 0.
40. Составить уравнение линии, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.
41 – 50. Линия задана уравнением r = r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой ситеме координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
41. 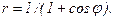
43. 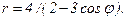
45. 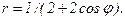
47. 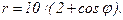
49. 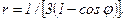
42. 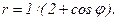
44. 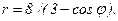
46. 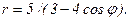
48. 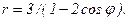
50. 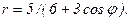
51 - 60. Дана система линейных уравнений:
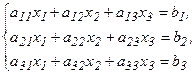
Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
51. 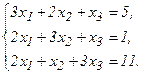 52.
52. 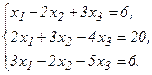
53. 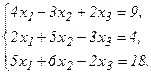 54.
54. 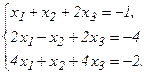
55. 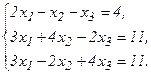 56.
56. 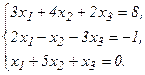
57. 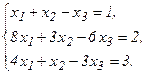 58.
58. 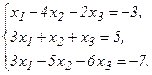
59. 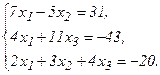 60.
60. 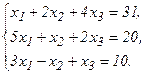
61 - 80. Решить систему трех уравнений с тремя неизвестными при помощи определителей.
61. 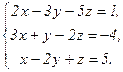 62.
62. 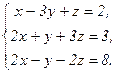
63. 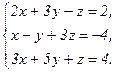 64.
64. 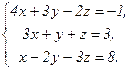
65. 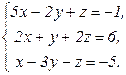 66.
66. 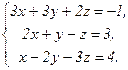
67. 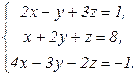 68.
68. 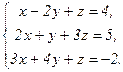
69. 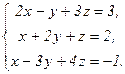 70.
70. 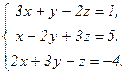
71. 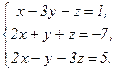 72.
72. 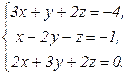
73. 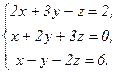 74.
74. 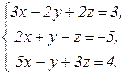
75. 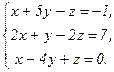 76.
76. 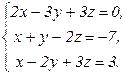
77. 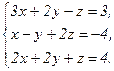 78.
78. 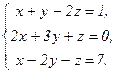
79. 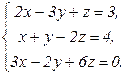 80.
80. 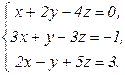
Date: 2015-04-23; view: 1190; Нарушение авторских прав