
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. 1. Определить абсолютные и относительные удлинения стержней и значение силы P = P1, при котором в наиболее напряженном стержне напряжения достигают предела
|
|
1. Определить абсолютные и относительные удлинения стержней и значение силы P = P 1, при котором в наиболее напряженном стержне напряжения достигают предела упругости. Заданная система (рис.20.4, а) один раз статически неопределима. Применяя метод сечений (рис.20.4, б) и составляя уравнения равновесия статики, последовательно можем определить:
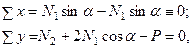
или
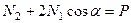 . (20.21)
. (20.21)

Рис. 20.4
Согласно деформированной схеме, изображенной на рис.20.4, а, из геометрических соображений, уравнения для определения относительных деформаций записываются в виде:
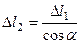 . (20.22)
. (20.22)
С учетом 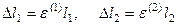 , и принимая во внимание, что на первом этапе нагружения все элементы заданной системы деформируются согласно закону Гука, т.е.
, и принимая во внимание, что на первом этапе нагружения все элементы заданной системы деформируются согласно закону Гука, т.е. 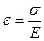 , получим:
, получим:
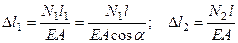 . (20.23)
. (20.23)
С учетом (20.23) из (20.21) и (20.22) можно получить следующую замкнутую систему уравнений относительно усилий N 1 и N 2:
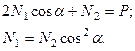
Откуда определяются:
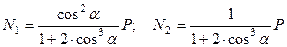 . (20.24)
. (20.24)
Для выражения напряжения в среднем в элементах заданной системы имеем:
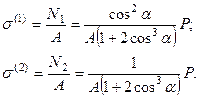 (20.25)
(20.25)
Откуда следует, что 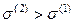 . Следовательно, в процессе нагружения сначала средний стержень переходит в пластическую стадию деформирования, а затем боковые стержни, т.е. при всех нагружения средний стержень, вплоть до стадии разрушения заданной системы, будет наиболее напряженным.
. Следовательно, в процессе нагружения сначала средний стержень переходит в пластическую стадию деформирования, а затем боковые стержни, т.е. при всех нагружения средний стержень, вплоть до стадии разрушения заданной системы, будет наиболее напряженным.
Принимая в (20.25), что 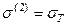 и P = P 1, окончательно получим:
и P = P 1, окончательно получим:
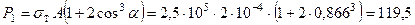 кН.
кН.
Абсолютные удлинения стержней принимают значения:
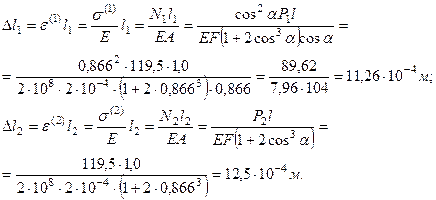
Относительные удлинения стержней принимают значения:
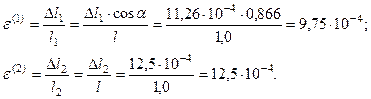
2. Определить абсолютные и относительные удлинения стержней и значение силы P = P 2, при котором все элементы заданной системы переходят в пластическую стадию деформирования. Физические уравнения взамен закона Гука в случае, когда стержни переходят в пластическую стадию деформирования, т.е. при 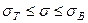 ,
, 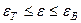 , в данном случае записываются в виде:
, в данном случае записываются в виде:
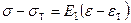 , (20.26)
, (20.26)
которое представляет собой уравнение прямой линии, описывающей диаграмму деформирования в области пластических деформаций (рис.20.4, в).
В начале по очевидным соотношениям определяется значение деформаций 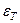 , соответствующее началу пластической стадии деформирования стержней и модуля деформаций в пластической стадии их деформирования:
, соответствующее началу пластической стадии деформирования стержней и модуля деформаций в пластической стадии их деформирования:
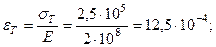
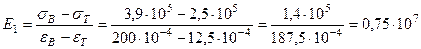 кН/м2.
кН/м2.
Заметим, что на данном этапе нагружения, т.е. когда 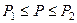 , боковые элементы заданной системы деформируются упруго, а средний элемент - будет находиться в пластическом состоянии.
, боковые элементы заданной системы деформируются упруго, а средний элемент - будет находиться в пластическом состоянии.
Учитывая, что при P = P 2 будем иметь 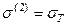 ,
, 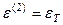 , последовательно определим значения усилий и абсолютное удлинение в боковых стержнях при их переходе в пластическую стадию деформирования:
, последовательно определим значения усилий и абсолютное удлинение в боковых стержнях при их переходе в пластическую стадию деформирования:
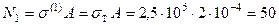 кН;
кН;
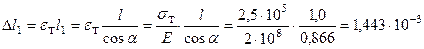 м.
м.
Учитывая выражения (20.22) и (20.26) определяется значение абсолютного и относительного удлинения, а также усилия в среднем стержне, в момент перехода боковых стержней в пластическую стадию их деформирования:
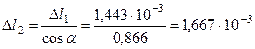 м;
м;
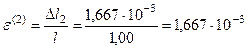 м;
м;
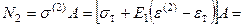
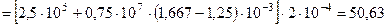 кН.
кН.
Далее из уравнения равновесия (20.21) вычисляется величина внешней силы P = P 2:
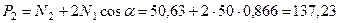 кН.
кН.
3. Определить абсолютные и относительные удлинения стержней и значение силы P = P 3, при котором в наиболее напряженном стержне напряжения достигают значения, равного временному сопротивлению 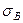 , т.е. при дальнейшем увеличении силы P происходит разрушение заданной системы. Сначала вычисляем значения удлинений в боковых стержнях, при достижении в среднем стержне предельных напряжений и деформаций
, т.е. при дальнейшем увеличении силы P происходит разрушение заданной системы. Сначала вычисляем значения удлинений в боковых стержнях, при достижении в среднем стержне предельных напряжений и деформаций 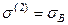 ,
, 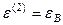 .
.
Учитывая, что 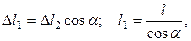 получим:
получим:
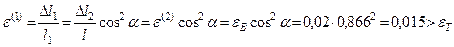 .
.
Таким образом, к моменту разрушения среднего стержня (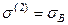 ,
, 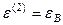 ) боковые стержни также находятся в пластической стадии деформирования. Напряжения в боковых стержнях, в момент разрушения среднего стержня, принимают значения:
) боковые стержни также находятся в пластической стадии деформирования. Напряжения в боковых стержнях, в момент разрушения среднего стержня, принимают значения:
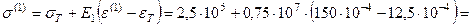
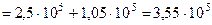 кН/м2.
кН/м2.
Для определения величины внешней силы P = P 3, т.е. значения силы в момент разрушения среднего стержня из уравнения равновесия (20.21) имеем:
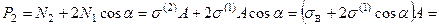
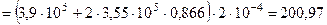 кН.
кН.
Как показывают результаты расчетов, для перехода среднего стержня в пластическую стадию деформирования необходима была внешняя сила P = P 1 = 119,5 кН, а для его разрушения - P = P 3 = 200,97 кН.
На основании полученных результатов можно заметить, что если бы мы ограничивались только учетом упругой стадии работы конструкции, т.е. P £ P 1, то несущая способность заданной системы оценивалась бы как P = P 1 = 119,5 кН.
Как показали расчеты, учет пластической стадии работы позволил выявить дополнительные резервы несущей способности заданной системы, т.к. величина разрушающей силы заданной системы в действительности равна P = P 3 = 200,97 кН.
В заключении определим величины абсолютных удлинений стержней в момент разрушения среднего стержня:
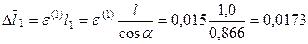 м;
м;
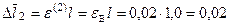 м.
м.
Легко определить во сколько раз абсолютные удлинения стержней возросли за счет возникновения пластических деформаций по отношению к их абсолютным удлинениям в момент перехода среднего стержня от упругой к пластической стадии деформирования:
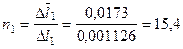 раз;
раз;
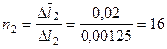 раз.
раз.
4. Рассматривая систему (рис.20.4, а) при отсутствии среднего стержня в процессе ее нагружения, определить абсолютные и относительные удлинения элементов системы, и внешней силы P = P 4, при котором в ее элементах напряжения достигают значения, равного временному сопротивлению 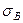 . Исключая средний стержень, система превращается из статически неопределимой в статически определимую. Применяя метод сечений, легко установить, что уравнения равновесия в данном случае принимают следующий вид:
. Исключая средний стержень, система превращается из статически неопределимой в статически определимую. Применяя метод сечений, легко установить, что уравнения равновесия в данном случае принимают следующий вид:
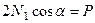 . (20.27)
. (20.27)
В конце упругой стадии работы элементов заданной системы имеем, что 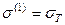 ,
, 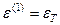 . С учетом данного обстоятельства последовательно определим значение усилия N 1, абсолютное удлинение стержней и величину силы P = P 1, соответствующих концу упругой стадии работы данной системы:
. С учетом данного обстоятельства последовательно определим значение усилия N 1, абсолютное удлинение стержней и величину силы P = P 1, соответствующих концу упругой стадии работы данной системы:
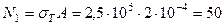 кН;
кН;
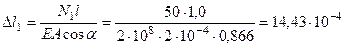 м;
м;
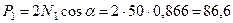 кН.
кН.
При дальнейшем нагружении системы, то есть при P > P 1 = 86,6 кН, элементы данной системы переходят в пластическую стадию деформирования. Последовательно определим значение внутренних усилий, абсолютных удлинений и величину разрушающей силы P = P 2, при достижении напряжений и деформаций предельных значений. Т.е. при 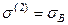 ,
, 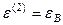 :
:
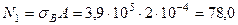 кН;
кН;
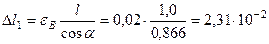 м;
м;
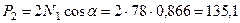 кН.
кН.
Анализируя полученные результаты, можно сделать следующие выводы.
Как и для трехстержневой статически неопределимой системы, так и для двухстержневой статически определимой системы, учет пластических деформаций позволил выявить дополнительные резервы систем по несущей способности. Если бы мы ограничились только упругим расчетом, расчетная несущая способность двухстержневой системы была бы равна P = P 1 = 86,6 кН. А за счет учета упруго-пластической работы элементов системы, как было показано, несущая способность будет исчерпана при P = P 2 = = 135,1 кН, т.е. при нагрузке в 1,56 раза больше, чем при упругом расчете.
Далее заметим, что за счет удаления одного среднего элемента из исходной системы, несущая способность и жесткость системы, соответственно, уменьшилась в 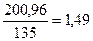 и в
и в 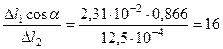 раз.
раз.
Date: 2015-05-22; view: 822; Нарушение авторских прав