Основные положения метода предельного равновесия

Расчет конструкций в упругой постановке задачи, как известно, проводится по методу допускаемых напряжений. Данный подход при расчете статически определимых и статически неопре­делимых систем не позволяет найти их истинный запас прочности, так как исчерпание несущей способности конструкции сопровож­дается появлением в ней пластических деформаций. Для выявления истинного запаса несущей способности конструкции необходимо проводить расчет с учетом упруго-пластических деформаций. Од­нако сложность аппарата теории пластичности не позволяет решать широкий круг очень важных инженерных задач. В этом отношении расчет конструкций по методу предельного равновесия, поз­воляет дополнить существующий пробел по данному вопросу. По­этому, метод расчета конструкций по предельным состояниям, по сравнению с упругим расчетом, является важным этапом для оцен­ки истинных запасов прочности конструкции. При этом следует отметить, что расчет конструкций по методу предельных состояний является приближенным в том контексте, что, в отличии от уп­руго-пластического расчета, не позволяет описать процесс перехода от упругого к предельному состоянию.

Если при проектировании инженерных сооружений необходи­мо знать процесс формирования напряженно-деформированного состояния вплоть до исчерпания несущей способности конструк­ций, метод предельного равновесия неприменим. Однако, в тех случаях, когда необходимо определить только несущую способ­ность конструкции этот метод является очень эффективным и имеет важное практическое значение.

При расчете конструкций по допускаемым напряжениям в упругой постановке задачи, как известно, предельной нагрузкой считается та, при которой наибольшее напряжение 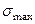, хотя бы в одной точке опасного сечения достигает величины 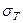. При этом вводится понятие о допускаемом напряжении, определяемом по формуле 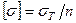, где n - коэффициент запаса.

При расчете конструкций по методу предельного равновесия предполагается двухстадийный характер деформирования материа­ла: в первой стадии материал подчиняется закону Гука, пока на­пряжения не достигнут предела текучести; а затем во второй ста­дии, предполагая, что в нем в определенной стадии нагружения в опасных сечениях беспредельно развиваются пластические дефор­мации при постоянном напряжении. С появлением пластических деформаций нарушается линейная зависимость между напряжениями и деформациями по закону Гука, и все расчетные формулы, вывод которых основан на этой зависимости, становятся неприменимыми. Нарушается прямая пропорциональность между действующими на элемент конструкции нагрузками и возникающими в нем напряжениями и деформациями. Становится неприменимым один из основных принципов сопротивления материалов – принцип независимости действия сил.

Так как зависимость между напряжениями и деформациями становится нелинейной и для каждого материала определяется видом диаграммы растяжения, единых для различных материалов расчетных формул, учитывающих пластические деформации, получить невозможно. При выводе расчетных формул диаграммы растяжения упрощают (схематизируют). Для материалов, имеющих площадку текучести, например для низкоуглеродистых сталей условная диаграмма зависимости на­пряжения от деформации состоит из наклонного и горизонтального участков и носит название диагpам­мы идеально yпpyго-плаcтичеcкого тела, или диагpаммы Пpандтля.

Суть метода состоит в том, что конструкция рассматривается в момент, непосредственно предшествующий ее разрушению, когда еще выполняются условия равновесия для внутренних и внешних сил, достигающих предельных значений. Отсюда и произошло наз­вание метода предельного равновесия.

Реальные конструкции представляют собой в большинстве слу­чаев многократно статически неопределимые системы, материал которых обладает свойством пластичности. Благодаря этому конст­рукции обладают дополнительными резервами несущей способнос­ти. После того, как в наиболее опасных сечениях напряжения до­стигают предела текучести, в отличие от статически определимых систем, статически неопределимые системы могут нести дополни­тельные нагрузки за счет перераспределения внутренних сил.

Для пластичного материала предельным обычно считается, на­пряженное состояние, которое соответствует возникновению замет­ных остаточных деформаций, а для хрупкого - такое, при котором начинается разрушение материала.

Для выполнения расчетов на прочность по методу предельного равновесия вводятся понятия ко­эффициента запаса прочности и эффективное напряже­ние.

Коэффициент запаса при данном напряженном состоянии это число, показывающее во сколько раз следует одновременно увели­чить все компоненты тензора напряжений, чтобы оно стало предельным.

Эквивалентное напряжение 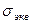- это такое напряжение, кото­рое следует создать в растянутом образце, чтобы его напряженное состояние было равноопасно с заданным.

Для пластичных материалов критерием наступления предельно­го состояния принимается состояние, при котором максимальные касательные напряжения достигают некоторого предельного значе­ния:

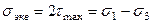. (20.1)

Гипотеза максимальных касательных напряжений, приемлемая для пластичных материалов, обнаруживает заметные погрешности для материалов, имеющих различные механические характеристики при сжатии и растяжении.

В таких случаях применяется энергетическая гипотеза, согласно которой предельное состояние в точке наступает тогда, когда энергия формоизменения

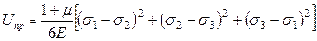(20.2)

принимает некоторое заранее заданное значение. Это предельное значение для 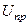определяется следующим образом. Для простого растяжения выражение (20.2) принимает вид:

.

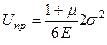В сложном напряженном состоянии 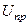принимает значение

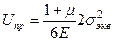. (20.3)

При совместном рассмотрении (20.2) и (20.3) получим:

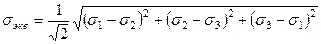или

.

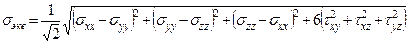Следует помнить, что расчет по методу предельного равновесия можно выполнять только для элементов конструкций, изготовленных из пластичных материалов, допускающих пластические деформации в наиболее напряженных точках без появления в них трещин. Недопустимо появление пластических деформаций в деталях машин, длительно работающих при переменных, циклических напряжениях, так как при этом резко снижается число циклов до разрушения, т.е. долговечность детали.