Вращательные и колебательные уровни молекул

В качестве модели двухатомной молекулы рассмотрим ротатор, т. е. два тела массы т, соединенных невесомым жестким стержнем. Определим, какие вращательные возбуждения (вращательные уровни) допустимы для него квантовой механикой. Выражение для оператора вращательной энергии нетрудно написать, используя известную из механики связь этой энергии с моментом импульса L:

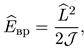(9.1)

где J — момент инерции ротатора. Из формулы (9.1) сразу видно, что энергия вращательного движения квантуется точно так же, как квадрат момента количества движения, т. е. спектр вращательных уровней имеет вид

.

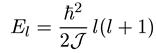(9.2)

Таким образом, вращательный спектр не эквидистантен, как у гармонического осциллятора, а расстояние между вращательными уровнями растет

по мере увеличения квантового числа l:

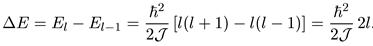
(9.3)

Теперь мы можем качественно описать характерные черты спектра возбуждений молекулы. Энергия стационарного состояния молекулы является суммой трех энергий — электронной (энергии электронов в атомах, образующих молекулу), энергии колебаний атомов друг относительно друга и вращательной энергии молекулы. Найдем относительный масштаб этих возбуждений.

Сначала рассмотрим энергию колебаний атомов в молекуле. На рис. 9.5 качественно показана зависимость потенциальной энергии взаимодействия атомов, образующих молекулу. Штрих-пунктиром изображена параболическая аппроксимация потенциальной ямы (гармоническое приближение).

Появление потенциальной ямы в энергии взаимодействия атомов есть следствие двух факторов:

на малых расстояниях одноименно заряженные ядра атомов отталкиваются, а на больших расстoяниях — притягиваются в результате обменного

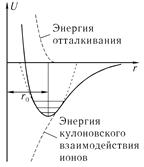
Pis 9.5

взаимодействия и сил статического или динамического диполь-дипольного взаимодействия. Для нас сейчас несущественна природа образования связанного состояния атомов в молекулах, мы можем рассматривать результат образования молекул просто как экспериментальный факт. Из измерений энергии диссоциации молекул следует, что минимум потенциальной энергии U₀= U(r₀) по порядку величины совпадает с энергией ионизации атомов, а размер молекул r₀ по порядку величины равен характерному размеру атомов α₀. В окрестности минимума потенциальная энергия U(r) может быть аппроксимирована параболой вида

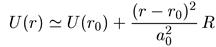, (9.4)

где R — постоянная Ридберга. Эта аппроксимация дает правильный порядок

необходимых нам величин: при смещении атомов на |r — r₀| = а₀ изменение

энергии взаимодействия порядка постоянной Ридберга, т. е. U(r) - U(r₀) = R.

Движение в параболической яме соответствует гармоническим колебаниям, и, чтобы найти энергию колебательного движения, необходимо оценить жесткость нашей системы. Как хорошо известно, энергия колебаний Е = kx²/2, где k— коэффициент жесткости системы, а x — смещение.

Отсюда следует, что в нашем приближении жесткость молекулы равна

k = 2R/a₀² (9.5)

Вспомним соотношение между боровским радиусом и постоянной Ридберга:

а₀ = ћ/(amc), R = α²mс²/2. (9.6)

Здесь α — постоянная тонкой структуры, а m — масса электрона. Подставляя эти выражения в (9.5), получаем

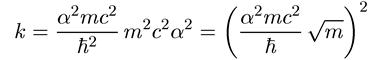
(9.7)

Теперь мы можем найти выражение для частоты колебаний атомов массы М

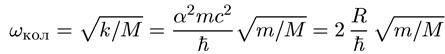. (9.8)

Характерная энергия возбуждений атомных электронов

ћω_e ~ R. (9.9)

Это означает, что энергия колебательного движения примерно в √(М/m) раз меньше. Так как масса атома по порядку величины в 103 раз больше массы электрона, а частота переходов лежит в видимой части спектра, то частоты колебательных возбуждений лежат в инфракрасной области (длины волн соответствующего излучения примерно в 30 раз больше длин волн видимого света).

Обратимся теперь к вращательной энергии. Согласно формуле (9.2) масштаб энергии вращательных уровней можно оценить из соотношения

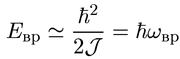
(9.10)

Поскольку J ~ Mα₀, то

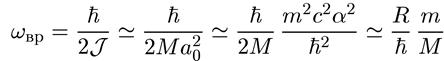
(9.11)

Таким образом, характерная частота вращательного движения еще в √(М/m) раз меньше, что соответствует далекой инфракрасой области спектра.

Теперь мы знаем соотношение между характерными частотами (энергиями) всех трех типов возбуждения:

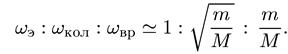
(9.12)

Рис. 9.6 уровни энергий молекулы

Схематически выглядят так, как это показано на рис. 9.6. На каждом электронном состоянии имеется эквидистантная полоса колебательных возбуждений, и, кроме того, на каждом колебательном уровне имеется еще вращательная полоса.

При возбуждении молекулы возникают целые серии переходов, образующих колебательно-вращательную полосу.

Теперь на квантовом языке очень легко объяснить комбинационное рассеяние света, которое часто называют рaмановским рассеянием по имени индийского физика Ч. Рамана, открывшего его одновременно с Л.И. Мандельштамом и Г.С. Ландсбергом. Комбинационное рассеяние представляет собой неупругое рассеяние фотонов, при котором фотон либо отдает молекуле часть своей энергии (стоксовая линия, частота рассеянного света равна

(ω₀-Δω), либо отбирает энергию у молекулы ((ω₀-Δω), антистоксовая линия).

Мы упомянули здесь комбинационное рассеяние, покольку оно является одним из основных экспериментальных методов исследования молекулярных спектров: спектры комбинационного рассеяния несут в себе информацию о колебательно-вращательных полосах молекул.

ГЛАВА 10

Date: 2015-05-19; view: 769; Нарушение авторских прав