Естественная и искусственная радиоактивность

Явление радиоактивности состоит в самопроизвольном распаде ядер с испусканием одной или нескольких частиц. Ядра, подверженные такому распаду, называются радиоактивными. Очевидно, что необходимым, но не всегда достаточным условием радиоактивного распада является его энергетическая выгодность — масса радиоактивного ядра должна превышать сумму масс ядра-осколка и частиц, вылетающих при распаде (совершенно очевидно, что аналогичное неравенство должно выполняться, если в нем

массы ядер заменить на массы соответствующих атомов, именно такие неравенства обычно и используют при рассмотрении радиоактивных распадов).

В природе существует большое число естественно-радиоактивных ядер, т. е. ядер, не успевших распасться с момента их образования до настоящего времени или непрерывно образующихся под действием космических лучей. В то же время радиоактивные ядра могут быть получены искусственным путем — бомбардировкой стабильных ядер частицами. Никакой физической границы между естественной и искусственной радиоактивностью нет.

Впервые радиоактивность была обнаружена А. Беккерелем в 1896 г. Незадолго до этого были открыты рентгеновские лучи, и Беккерель изучал связь флюоресценции с рентгеновским излучением. Способные флюоресцировать соли урана помещались на фотопластинку, завернутую в черную бумагу, и ставились на солнечный свет. Считалось, что под действием солнечных лучей уран флюоресцирует, и, если в состав спектра флюоресценции входят рентгеновские лучи, то, проходя через черную бумагу, они будут вызывать почернение пластинки. Несколько дней не было солнца, и подготовленные

пластинки с ураном пролежали в черном ящике. Тем не менее после проявления было обнаружено сильное почернение пластинок. Таким образом выяснилось, что соли урана сами испускают какие-то лучи.

Очень скоро к исследованию этого явления подключились другие ученые. 1898 г. П. Кюри совместно с М. Склодовской-Кюри открыли новые радиоактивные элементы — полоний и радий. Используя разработанный ими метод обогащения, они смогли в 1902 г. путем кропотливой работы по переработке больших количеств урановой смолки получить несколько дециграммов чистой соли радия. В 1903 г. за исследования явления радиоактив-

ности супруги Кюри совместно с А. Беккерелем были удостоены Нобелевской премии по физике. Сам термин «радиоактивность» был введен в науку. Склодовской-Кюри.

Законы радиоактивного распада. Радиоактивный распад характеризуется временем протекания, сортом испускаемых частиц, их энергией, а ри вылете нескольких частиц — угловой корреляцией, т. е. относительным углом между направлениями их вылета. Исходное радиоактивное ядро называется материнским, продукт его распада — дочерним.

Поскольку процесс распада происходит самопроизвольно (спонтанно), то изменение dN числа ядер N из-за распада за произвольный промежуток времени dt определяется только количеством радиоактивных ядер в момент t и пропорционально промежутку времени dt:

-dN = λNdt, (10.34)

где λ — постоянная, характеризующая скорость распада. Интегрируя (10.34)

и считая, что при t = 0 количество ядер равно исходному N = N₀, получаем

N = N₀е^-λt (10.35)

т. е. число ядер убывает по экспоненциальному закону.

Величина А, определяющая в (10.35) скорость убывания количества радиоактивных ядер, называется постоянной распада. Она имеет размерность [с^-1] и, как будет показано чуть дальше, характеризует вероятность распада одного атома в одну секунду. Для характеристики радиоактивных элементов вводится также понятие периода полураспада Т_1/2. Под ним понимается время, в течение которого распадается половина наличного числа атомов.

Впервые закон радиоактивного распада (10.35) был установлен в 1903 г. П. Кюри. Он же ввел понятие периода полураспада и показал его независимость от внешних условий. Исходя из этого, П. Кюри предложил использовать период полураспада как эталон времени для определения абсолютного возраста земных пород.

Рассчитаем теперь среднее время жизни радиоактивного ядра. Подставляя

условие N(T_1/2) = N₀/2 в уравнение (10.35), получим

N₀/2 = N₀e^-λTl/2, (10.36)

откуда, логарифмируя, найдем, что

λТ_1/2 = 1n2 = 0,693,

а период полураспада

Т_1/2 = 0,693/λ. (10.37)

При экспоненциальном законе радиоактивного распада в любой момент времени t имеется отличная от нуля вероятность найти еще нераспавшиеся ядра. Время жизни таких ядер превышает t. Вместе с тем, другие, распавшиеся к этому времени ядра, прожили разное время, меньшее t. Среднее время жизни для данного радиоактивного изотопа определяется обычно следующим образом:

(10.38)

Следовательно, среднее время жизни г радиоактивного ядра равно обратной величине от постоянной распада А. За время т первоначальное число ядер уменьшается в е раз.

Величина

А = - dN/dt = λN

называется активностью данного препарата,

она определяет число распадов в секунду. Активность является характеристикой определенного количества распадающегося вещества, а не отдельного ядра. Единицей активности является беккерелъ: 1 беккерель (Бк) равен 1 распаду в секунду. Часто на практике используют и внесистемную, ранее применявшуюся, единицу активности — кюри: 1 кюри (Ки) равно числу распадов ядер, содержащихся в 1 г радия за 1 с 3,7 • 10¹⁰ распадов в секунду).

Виды радиоактивных распадов. К числу радиоактивных процессов относятся α- и β-распады (в том числе и захват электрона с атомной оболочки), γ-излучение, деление ядер, а также испускание запаздывающих нейтронов и протонов. Два последних процесса относятся к каскадному двухступенчатому типу, так как испускание запаздывающих нейтронов (протонов) происходит после предварительного испускания ядром электрона (позитрона). Поэтому испускание запаздывает на время, характеризующее предшествующий β-распад. Рассмотрим перечисленные нами процессы.

Альфа-распад. Спонтанному α-распаду подвержены только тяжелые ядра с Z > 83 и небольшая группа редкоземельных ядер в области А = 140-160. При α-распаде исходное материнское ядро испускает ядро гелия (α-частицу) и превращается в дочернее ядро, числа протонов и нейтронов у которого уменьшаются на две единицы каждое. Период полураспада α-активных ядер изменяется в чрезвычайно широких пределах. Так, например, для изотопа полония ²¹⁴ ₈₄Pо он равен 3 • 10^~7 с, а для изотопа свинца ²⁰⁴₈₂Pb — 1,4 * 10¹⁷ лет. Диапазон изменения энергии вылетающих α-частиц значительно меньше — от 4 до 9 МэВ, причем чем меньше их энергия, тем больше период полураспада. Функциональная связь между энергией α-частицы Е и периодом полураспада радиоактивного ядра T_1/2 хорошо

описывается формулой

lgT_1/2 = а/√Ё + b, (10.39)

полученной на основе экспериментальных данных Г. Гейгером и Дж. Нэттолом в 1911 г. Теоретическое обоснование закон Гейгера-Нэттола получил лишь после создания квантовой механики в 1928 г. в работах Г. Гамова и, независимо, Р. Герни и Э. Кондона, которые показали, что вероятность вылета α-частицы из ядра определяется вероятностью ее проникновения через кулоновский барьер. Экспоненциальный характер этого процесса возникает вследствие экспоненциального затухания волновой функции в области под

барьером, где потенциальная энергия больше энергии частицы.

Четыре элементарные частицы, из которых состоит α-частица (два протона и два нейтрона), участвуют в сложном движении нуклонов в ядре, и нет никакого способа отличить их от других частиц этого ядра. Вместе с тем существует заметная (~ 10^~6) вероятность образования а-частицы в ядре на какое-то короткое время в результате случайного сближения четырех нуклонов. Однако лишь только когда а-частица покинет ядро и окажется достаточно далеко от него, можно рассматривать ее и ядро как две отдельные частицы.

Энергетически α-распад возможен, если энергия связи исходного материнского ядра Е_{А, z} меньше суммы энергий связи дочернего ядра Е_{А-4, z-2} и α-частицы Е_α, т. е. должно выполняться соотношение

ΔE = Е_{А-4, z-2} + E_α - Е_{А, z} > 0. (10.40)

Энергия связи α-частицы равна 28 МэВ, что составляет 7 МэВ/нуклон.

Поэтому невозможен α-распад средних ядер, у которых энергия связи на

нуклон ~ 8 МэВ.

Рассмотрим вид потенциальной энергии а-частицы в ядре и его окрестности (рис. 10.9). Вне ядра короткодействующие ядерные силы быстро обращаются в нуль, и на а-частицу действует только электростатическое кулоновское отталкивание, потенциал которого U_кул равен

U_кул = 2(Z-2)e²/r (10.41)

На границе ядра вступает в игру сильное притяжение, обусловленное ядерными силами, и потенциальная кривая резко уходит вниз. Внутри ядра потенциал можно считать примерно постоянным.

Даже если полная энергия а-частицы в ядре больше нуля, как это показано на рис. 10.9, и тем самым энергетически а-распад разрешен, по представлениям классической физики этот процесс не может происходить без сообщения ей дополнительной энергии, поскольку частица находится в потенциальной яме. Однако квантовая механика разрешает прохождение или, точнее, просачивание частицы через потенциальный барьер. Говорят, что может происходить туннелирование α-частицы сквозь барьер. Дело в том, что

свойства квантовой частицы описываются с помощью волновой функции ψ, квадрат модуля которой |ψ(r)|² пропорционален вероятности обнаружить частицу в точке r. В

случае конечного потенциала (потенциала со стенками конечной высоты) ψ-функция

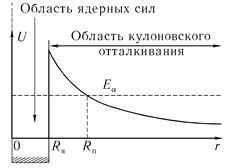
Рис. 10.9

всюду отлична от нуля. Поэтому существует, хотя и малая, вероятность обнаружить частицу вне ядра, а это и означает возможность α-распада.

Покажем качественно, откуда следуют указанные выше закономерности α-распада. Проницаемость D барьера для α-частицы с энергией Е определяется следующим выражением:

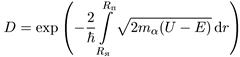(10.42)

где интегрирование производится в пределах от радиуса ядра R_я до точки поворота R_n, определяемой из условия

2(Z–2)e²/R_n = Е

(мы учли, что на α-частицу вне ядра действует кулоновский потенциал ядра-остатка с зарядом Z-2). Будем считать, что туннелирование происходит глубоко под барьером, т. е.

U >> Е.

В силу малости постоянной Планка, стоящей в выражении для проницаемости барьера в экспоненте, фактически вклад области, где U ~ Е, мал, и накладываемое нами условие физически оправдано. При этих предположениях формула (10.42) принимает вид

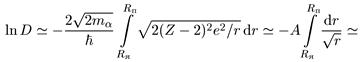
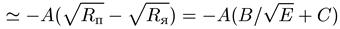
(10.43)

где А, В, С — константы. Поскольку период полураспада Т_1/2 обратно пропорционален проницаемости барьера, из выражения (10.43) следует экспериментально наблюдаемый закон Гейгера-Нэттола

lgT_1/2 = а/√Е + b, (10.44)

связывающий период полураспада с энергией вылетающей α-частицы. Реально коэффициенты а и b — не константы, однако они очень слабо зависят от атомного номера материнского ядра Z:

а ~ 1,6 Z; b ~ -1,6 Z^2/3 - 21,4 (10.45)

(если Т_1/2 выражается в секундах, Е — в мегаэлектронвольтах, a Z — заряд дочернего ядра). Как видно, Т_1/2 не зависит от атомного веса А, слабо зависит от Z и в сильной степени — от энергии вылетающих α-частиц.

До сих пор мы говорили только о проницаемости потенциального барьера.

Чтобы найти константу распада λ надо умножить проницаемость барьера на число попыток α-частицы ν в единицу времени преодолеть этот барьер, т. е.

λ= 0,693/T_1/2 = νD. (10.46)

Грубая оценка предэкспоненциального множителя в (10.46) может быть сделана, если под v понимать частоту ударов а-частицы о поверхность ядра, определяемой формулой

ν = v/(2R_n), (10.47)

где v — скорость а-частицы внутри ядра. Разумеется, предэкспоненциальный множитель также зависит от энергии (согласно нашей грубой оценке он пропорционален √Е), но, по сравнению с экспоненциальной зависимостью, это — медленно меняющаяся функция энергии, так что именно проницаемостью барьера определяются

все основные закономерности α-распада.

Энергетический спектр а-частиц многих α-активных ядер состоит из нескольких линий, одна из которых является преобладающей. В качестве примера на рис. 10.10 показан α-спектр ThC(²¹²₈₃Bi).

Рис. 10.10 α-спектр ThC(²¹²₈₃Bi).

Дискретность линии и их относительная интенсивность легко объяснимы. Дело в том, что α-частицы могут либо испускаться ядром, находящимся в возбужденном состоянии (так называемые длиннопробежные α-частицы), либо может происходить α-распад из сновного состояния материнского ядра в возбужденные состояния дочернего ядра (короткопробежные α-частицы). На рис. 10.11 приведены два примера таких переходов — распад ²³⁸Рu и ²¹²Ро.

В первом случае(²³⁸Рu) α-частицы максимальной энергии соответствуют переходам из основного в основное состояние. Кроме того, α-распад может идти в возбужденные состояния дочернего ядра ²³⁴U с последующими γ~переходами в основное состояние. Распад ²¹²Ро — пример испускания α-частиц из возбужденного состояния. Такая ситуация возникает от того, что ²¹²Ро образуется в результате β-распада ²¹²Bi. Находясь в возбужденном состоянии, ядро ²¹²Ро может либо испустить α-частицу, либо путем γ-излучения перейти в основное состояние.

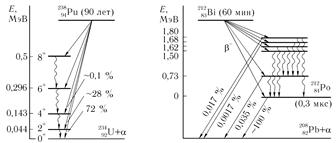
Рис. 10.11

Бета-распад. Бета-распад — процесс самопроизвольного превращения нестабильного ядра в ядро-изобару (ядро с тем же атомным номером) с зарядом, отличным от исходного на ΔZ = ±1, за счет испускания электрона (позитрона) или захвата электрона с атомной оболочки. Главной особенностью β-распада является то, что он обусловлен не ядерными и не электромагнитными силами, а слабым взаимодействием (см. гл. 12), вероятность

которого примерно в 10¹⁴ раз меньше ядерного. Поэтому периоды полураспадов

β-активных ядер в среднем довольно велики — порядка нескольких минут и даже часов. В общем случае при прочих равных условиях при β-распаде соблюдается та же тенденция, что и при α-распаде: чем больше энергия Q, выделяющаяся при распаде, тем меньше период полураспада.

Периоды полураспада меньше 10^~2 с не встречаются, так как при них значения Q получились бы больше 10 МэВ, т. е. больше средней энергии связи нуклонов в ядре; при таком избытке энергии ядро оказывается нестабильным по отношению к вылету нуклона, а этот процесс (когда он возможен) происходит гораздо быстрее β-распада, за время порядка 10~20 с. Процессы β-распада идут всегда, когда они энергетически возможны. Кулоновский барьер для β-распада несущественен в силу очень малой массы электрона.

Характерной особенностью β -распада является энергетический спектр вылетающих частиц (рис. 10.12). В отличие от а-частиц, в данном случае мы имеем непрерывный энергетический спектр электронов β-распада. Наблюдающаяся непрерывность является следствием участия в процессе распада еще одной частицы — нейтрино, обладающей нулевой энергией покоя (согласно последним данным верхний предел энергии покоя нейтрино составляет 3 эВ). Поэтому при одиночном акте распада соотношение энергий электрона и нейтрино может быть любым, т. е. энергия электрона может принимать любые значения от нуля до максимальной возможной энергии (полной выделяющейся энергии).

Остановимся более подробно на энергетических процессах при β-распаде.

Рассмотрим атом с зарядом Z+1 и полной энергией E_z+1. Пусть его нулевая энергия соответствует системе «однократно ионизованный атом плюс покоящийся свободный электрон». Последнее означает, что энергия нейтрального атома с зарядом Z + 1 слегка отрицательна и имеет порядок энергии

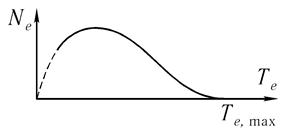
Рис. 10.12

ионизационного потенциала атома (рис. 10.13). При этом возможны следующие случаи.

А. Энергия E_z атома с зарядом Z выше, чем E_z+1. Энергетически возможным является β-распад, т. е. распад с вылетом электрона, и атом Z переходит в ионизованный атом Z + 1. Процесс E_z+1 -> E_z запрещен.

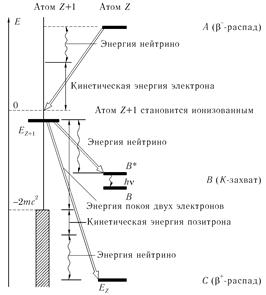
Рис. 10.13

B. Переход E_z+1 —> E_z возможен только в том случае, если ядро Z + 1 поглощает электрон из атомных К-, L-, М-оболочек. Обычно ядром захватывается К-электрон, и поэтому процесс часто называют К-захватом. Новый атом Z образуется в возбужденном состоянии B* соответственно с вакансией (дыркой) в К- или L-оболочке. Затем роисходит переход в основное состояние, сопровождающийся испусканием характеристического излучения:

B* -> В + hv. (10.48)

C. Энергия атома Z такова, что E_z + 2m² <= E_z+1. Также возможен процесс К-захвата, но, кроме того, ядро может претерпевать β⁺-распад (позитронный распад). Приведенное энергетическое соотношение легко получить.

Если m— масса электрона (позитрона), M_z — масса конечного ядра, а

M_z+1 — масса исходного ядра, то должно выполняться неравенство

M_z+1 c² >= M_zc² + mс². (10.49)

Но массы атомов (^AM_Z и ^AM_z+1) Z и Z+1 с учетом массы электронов равны

^AM_Z =M_Z+ Zm, ^AM_Z+1 = M_z+1 + (Z + l)m. (10.50)

Подставив эти соотношения в условие A0.49), получим

^AM_Z+1 >=^AM_z+2m (10.51)

или

E_z+1 >= E_z +2mc². (10.52)

Важно подчеркнуть, что β-распад — процесс не внутриядерный, а внутринуклонный. В ядре распадается одиночный нуклон — нейтрон либо протон.

Электронный распад связан с распадом нейтрона

n° -> p⁺ + e^- + ν^>. (10.53)

При позитронном распаде в ядре распадается одиночный протон

р⁺ -> n° + е⁺ + ν. (10.54)

В формуле (10.53) знак «тильда» над нейтрино означает, что при распаде нейтрона образуется антинейтрино. Почему так происходит, будет подробно рассматриваться дальше в гл. 12. Заметим, что в свободном состоянии нейтрон нестабилен, его период полураспада равен 10,5 мин. Свободный же протон не распадается, т. к. его масса меньше массы нейтрона, но для связанного в ядре протона подобное превращение возможно, недостающая энергия восполняется ядром.

С β-распадом связано одно из удивительных открытий XX в. — открытие несохранения четности. Кажется совершенно очевидным, что выбор системы координат, в которой математически записываются физические уравнения и происходит, соответственно, эволюция системы во времени, является вполне произвольным. Следовательно, не может быть разницы между описаниями одного и того же процесса в левой и правой системах координат. Математически это означает, что все уравнения должны быть симметричны относительно операции пространственной инверсии, т. е. замены r на -r. Изменение

знаков координат какой-либо точки соответствует положению точки, полученной в результате ее зеркального отражения в трех координатных плоскостях, и поэтому такое изменение системы координат можно трактовать как переход к совокупности событий, являющихся зеркальным изображением данной совокупности событий. Преобразование

пространственной инверсии обладает физическим смыслом вследствие того, что, как показывает опыт, процессы природы в основном симметричны относительно

такого преобразования. Это означает, что для всякого процесса в природе осуществляется и протекает с той же вероятностью «зеркально симметричный» процесс.

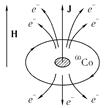
рис 10.14

Симметрия относительно преобразования пространственной инверсии приводит при квантовомеханическом описании к существованию у системы определенной пространственной четности. Иными словами, волновая функция системы либо четна, либо нечетна при этом преобразовании. Пространственная четность сохраняется в процессах сильного и электромагнитного взаимодействий. Что же касается слабых взаимодействий,

ответственных за β-распад, то здесь ситуация иная. Гипотеза несохранения четности в слабых взаимодействиях была выдвинута Т.Д. Ли(р.1926) и Ч.Н. Янгом(р.1922), которые предложили соответствующий эксперимент, поставленный Ч.С. By(р.1913).

Принципиальная схема опыта крайне проста. Бета-активный изотоп ⁶⁰Со помещался в магнитное поле Н соленоида, которое поляризовало ядра кобальта, т. е. ориентировало их магнитные моменты вдоль поля (рис. 10.14).

Вся система зеркально симметрична относительно плоскости токового витка, поэтому, казалось бы, и интенсивность излучения β-электронов должна быть одинаковой по обе стороны от плоскости симметрии. На самом деле в эксперименте наблюдалась резкая асимметрия (примерно на 40 %), т. е. асимметрия слабых взаимодействий относительно левого и правого.

Гамма-излучение. В том случае, когда распад ядра с вылетом нуклона энергетически невозможен, происходит снятие возбуждения за счет испускания γ-квантов — высокоэнергетичных фотонов. Испускание ядром γ- квантов с энергией, превышающей энергию связи нуклона, имеет место только в случае запрета по четности и моменту количества движения для вылета нуклонов (или других частиц), который делает процесс испускания γ-квантов относительно более вероятным. Если же подобного рода запрета не существует, то испускание таких «ядерных» частиц, как нейтроны, протоны,

а-частицы, значительно более вероятно, чем γ-uзлучение. Последнее связано с тем, что γ~излучение обусловлено электромагнитным взаимодействием, тогда как вылет нуклонов или а-частиц просходит благодаря более сильному ядерному взаимодействию (этот тип фудаментального взаимодействия обычно называют сильным взаимодействием — см. гл. 12).

В отличие от β-распада, γ~излучение — явление не внутринуклонное, а внутриядерное. Изолированный свободный нуклон не может испустить (или поглотить) γ- квант из-за совместного действия законов сохранения энергии и импульса. Последнее полностью аналогично тому, что фотоэффект на свободных электронах невозможен. В то же время внутри ядра нуклон может испустить квант, передав при этом часть импульса другим нуклонам.

В гл. 8 мы показали, что поскольку фотон — безмассовая частица, для него не существует системы координат, в которой он покоится. Кроме того, для фотона бессмысленно делить его полный момент импульса на спиновый и орбитальный. Полный же момент может иметь в принципе любое целое (в единицах К) значение, начиная с единицы. Именно поэтому часто говорят, что спин фотона равен 1, хотя более правильным является утверждение «минимальное значение момента импульса фотона равно 1».

Как упоминалось в § 8.1, состояние фотона, испущенного какой-либо системой, характеризуют мулътиполъностъю, т. е. определенными полным моментом импульса и четностью.

Фотон мультипольности 2^L обладает угловым моментом L, абсолютное значение которого, согласно квантовой механике, равно √(L(L + 1)), т. е. точно такое же, как и в случае частицы конечной массы. В соответствии с законом сохранения момента импульса должно выполняться следующее соотношение между моментами I_н и I_К начального и конечного ядра и моментом L, уносимым γ-квантом:

|I_н-I_к|<=L<=I_H + I_K. (10.55)

Оно является правилом отбора по моменту количества движения. Согласно (10.55) дипольные γ-кванты (L = 1) могут быть испущены при переходах между состояниями с

ΔI = 0, ±1, кроме (0-0)-переходов; квадрупольные γ-кванты (L = 2) — при переходах между состояниями с ΔI = ± 2, ±1, 0, кроме (0-0)-, (0-1)- и (1-0)-переходов и т. д.

Еще одно правило отбора связано с выполнением закона сохранения четности волновой функции. Четность, как мы уже говорили ранее, определяется по влиянию на знак волновой функции системы отражения всех трех осей относительно начала координат.

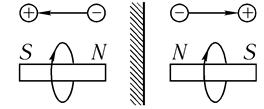
рис 10.15

Такое отражение в случае статического диполя приводит к взаимной перестановке положения каждого заряда (рис. 10.15). Следовательно, если смотреть из исходной системы координат, то происходит очевидное изменение знаков всех зарядов. Однако такое же отражение в случае магнитного диполя (кругового тока) не изменяет направления (знака) тока в магнитном диполе (см. также рис. 8.1).

Поэтому разрешенное изменение четности ядра, испускающего электрическое γ-излучение мультипольности L, описывается формулой

Р_и/Р_к = (-1)^L, (10.56)

а для ядра, испускающего магнитное L-мультипольное излучение, формулой

Р_н/Р_к = (-1)^L+1, (10.57)

где Р_н иР_к — соответственно четности начального и конечного состояний ядра.

Часто снятие возбуждения в ядре происходит не путем непосредственного перехода в основное состояние, а путем испускания каскада γ-квантов, обладающих меньшей мультипольностью. При этом оказывается, что существует угловая корреляция последовательно испускаемых γ-квантов, т. е. наблюдается преимущественное направление испускания второго кванта.

Появление корреляционной зависимости обусловлено тем, что проекция т полного момента γ-кванта на его импульс может принимать только значения m = ±1 (единицей измерения является постоянная Планка ћ).

Значение m = 0 исключено условием поперечности электромагнитных волн.

Поэтому, если, например, ядро на уровне с моментом нуль испустило γ-квант, вылетевший в определенном направлении, т. е. зарегистрированный в этом направлении детектором, то проекция спина ядра в новом, более низком энергетическом состоянии на данное направление может быть только ±1, но не нуль. Таким образом, оказывается, что ядро ориентировано в пространстве уже не совсем хаотически. Поэтому и каскадные γ-кванты вылетают из него в разных направлениях с разной вероятностью. Угловая

корреляция существенно зависит от моментов последовательно распадающихся состояний.

Времена жизни γ-активных ядер в среднем невелики и обычно имеют порядок 10^~7-10^~11 с. В редких случаях, при сочетании высокой степени запрета с малой энергией перехода, могут наблюдаться γ-активные ядра с временами жизни макроскопического порядка — до нескольких часов, а иногда даже лет. Такие возбужденные долгоживущие состояния ядер называются изомерами. Данное явление было открыто в 1935 г. И.В. Курчатовым с сотрудниками. Изомерный уровень должен иметь спин, сильно отличающийся от спинов уровней, лежащих ниже, и низкую энергию возбуждения. Как правило, изомерное состояние относится к первому возбужденному уровню ядра. Так, например, в ядре ¹¹⁵₄₉In, основное состояние имеет характеристику 9/2⁺, а первый возбужденный уровень с нергией 335 кэВ — характеристику 1/2^~. Переход этот настолько сильно запрещен, что время жизни возбужденного уровня оказывается равным 14,4 часа.

Следует обратить внимание на то, что все лабораторные источники γ-квантов являются фактически долгоживущими β-активными ядрами, а γ-излучение возникает из-за

β-распада материнского ядра на возбужденные уровни дочернего ядра. Так, например, в широко распространенном источнике γ-излучения ⁶⁰Со (Т_1/2 = 5,3 г) происходят вылет электронов с энергией 0,3 МэВ и последующие γ-переходы в ядре ⁶⁰Ni с энергиями 1,17 и 1,33 МэВ.

Кроме γ-излучения, существует еще один механизм потери энергии возбужденным ядром — испускание электронов внутренней конверсии. В этом процессе энергия возбуждения ядра передается непосредственно одному из орбитальных электронов, который получает всю энергию кванта. С наибольшей вероятностью процесс внутренней конверсии идет на К-электронах, волновая функция которых больше всего перекрывается с ядром. Однако

если энергия, освобождаемая при ядерном переходе, меньше энергии связи Х-электрона, то наблюдается конверсия на L-электронах и т. д. Помимо конверсионных электронов, при внутренней конверсии можно наблюдать еще и рентгеновские кванты, возникающие при переходе одного из наружных электронов на уровень К- или L-оболочки, освобожденной вылетевшим электроном. Моноэнергетичность вылетающих при внутренней конверсии электронов позволяет отличать их от β-распадных электронов, спектр которых непрерывен.

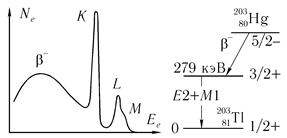
рис. 10.16

В качестве иллюстрации этого процесса на рис. 10.16 приведен спектр электронов, вылетающих из β-активного ядра ртути ²⁰³Hg.

Процесс внутренней конверсии в некотором смысле аналогичен колебаниям в связанной системе с двумя степенями свободы. Простейшим примером такой системы могут служить два маятника, связанные пружиной: колебания одного из маятников благодаря пружине возбуждают колебания другого. В случае внутренней конверсии роль «пружины» играет электрическое поле. Таким образом, внутренняя конверсия представляет собой первичный, а не вторичный процесс взаимодействия электромагнитного излучения с орбитальными электронами: энергия возбуждения ядра передается орбитальным электронам, как говорят, виртуальными, а не реальными квантами.

Деление ядер. Деление атомных ядер — это процесс, характерный только для самых тяжелых ядер, начиная от тория и далее в сторону больших Z.

Сейчас трудно себе представить, с каким недоумением и недоверием физики встретили в 1938 г. сообщение О. Хана и Ф. Штрассмана о делении атомного ядра медленными нейтронами, поскольку было хорошо известно, что для вырывания из ядра одного нуклона требуется энергия в миллионы электроновольт. По образному выражению Р. Личмена, это равносильно тому, что твердый камень раскалывается от легкого постукивания карандаша. Первое объяснение наблюдаемого процесса было выдвинуто Н. Бором и Дж. Уилером и независимо, Я.И. Френкелем уже через несколько месяцев на основе

аналогии деления ядра с делением заряженной капли жидкости при деформации.

При попадании нейтрона ядро-капля начинает колебаться и в какой-то момент времени принимает вытянутую форму. Действующие между нуклонами ядерные силы, подобно силам сцепления молекул в жидкости, приводят к появлению поверхностного натяжения. Они стремятся вернуть ядру первоначальную почти сферическую форму (тяжелые ядра в основном состоянии слегка деформированы и имеют форму вытянутого эллипсоида).

Однако, если вытянутость ядра в какой-то момент времени оказывается достаточно большой, электростатические силы отталкивания одноименных зарядов могут превзойти силы поверхностного натяжения.

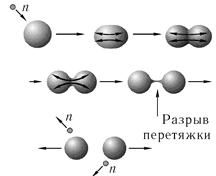
Тогда ядро начнет еще больше растягиваться, пока не разорвется на два осколка. В качестве «мелких брызг» в момент деления вылетают два-три нейтрона, α-частицы и даже легкие ядра, правда, с очень малой вероятностью. Последовательные стадии процесса

деления атомного ядра представлены на рис. 10.17.

Pис.10.17

В 1940 г. Г.Н. Флеров и К.А. Петржак обнаружили, что ядра урана могут делиться и самопроизвольно (спонтанно). Период полураспада спонтанного деления ²³⁸U

равен 8 • 10¹⁵ лет. Как оказалось в дальнейшем, все ядра тяжелее тория испытывают спонтанное деление, причем чем тяжелее ядро, и чем больше его заряд, тем в среднем больше вероятность этого процесса, т. е. тем меньше период его спонтанного деления. Период спонтанного деления очень быстро уменьшается по мере перехода к более тяжелым ядрам. Так, у изотопа плутония ²⁴²Рu он равен 6,8*10¹⁰ лет, у калифорния ²⁵²Cf уже 85 лет, а у фермия ²⁵⁶Fm – 2.7 часа.

Спонтанное деление ядер представляет собой чисто квантовомеханический эффект. Как указывалось выше, оно является результатом конкуренции двух процессов — поверхностного натяжения, стремящегося вернуть ядро в исходное состояние, и кулоновского отталкивания заряженных осколков. Таким образом у ядра появляется потенциальный барьер, препятствующий его делению.

На рис. 10.18 показана потенциальная энергия ядра как функция отклонения ΔR поверхности ядра от сферической формы. Основное состояние ядра является слегка

деформированным.

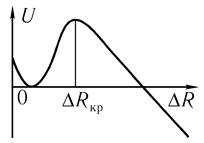
pис. 10.18

Следовательно, спонтанное деление ядер является туннельным процессом, точно так же, как это происходит при туннелировании α-частиц. Отсюда и появляется столь сильная зависимость периода спонтанного деления от заряда ядра: по мере увеличения заряда ядра уменьшается величина барьера и резко увеличивается вероятность деления. У изотопа ²³⁵U барьер деления равен примерно 6 МэВ, как раз той энергии, какую вносит медленный нейтрон в ядро, и поэтому ²³⁵U столь легко делится при поглощении нейтрона.

Появление и влияние кулоновского барьера легко объясняется с помощью полуэмпирической формулы Вайцзеккера для энергии связи ядер. Пусть ядро изменяет свою форму, например, из сферического становится эллипсоидальным. Объем ядра не изменяется (ядерная материя практически несжимаема), но поверхность увеличивается, а кулоновская энергия уменьшается (увеличивается среднее расстояние между протонами). Способность ядра к делению естественно характеризовать отношением кулоновской энергии к поверхностной, т. е.

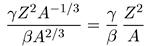(10.58)

Так как коэффициенты γ и βпостоянны для всех ядер, то вероятность деления определяется величиной Z²/А, которая по предложению Бора и Уиллера выбрана в качестве параметра делимости ядра. Расчеты показывают, что для ядер с Z² /А >= 49 деление происходит практически мгновенно, за время порядка 10^~23 с.

Это означает, что спонтанное деление определяет предел существования стабильных ядер, т. е. у ядер с Z >= 120 отсутствует энергетический барьер, препятствующий спонтанному делению. Характер изменения барьера деления E_f и энергии Q_f, выделяющейся при делении ядра, по мере деформации ядра ε. При разных значениях параметра делимости показан на рис. 10.19, а на рис. 10.20 приведены времена жизни для спонтанного деления четно-четных ядер. Ядра с нечетными N или Z имеют на несколько порядков больший период полураспада для спонтанного деления, чем соседние четно-четные ядра.

На основе приведенных выше рассуждений легко предсказать следующие основные свойства процесса деления.

1. При делении тяжелого ядра должна освобождаться большая энергия Q, поскольку энергия связи, приходящаяся на один нуклон в тяжелых ядрах ε_тяж примерно на 0,8 МэВ меньше сответствующей энергии ε_ср для средних ядер; так, например, для ядра ²³⁸U

Q_f ~ А(ε_тяж - ε_ср) ~ 238 • 0,8 ~ 200 МэВ. (10.59)

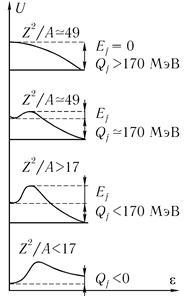
Рис. 10.19

2. Подавляющая часть энергии деления освобождается в форме кинетической энергии осколков деления Ек, так как ядра-осколки неизбежно должны разлетаться под действием кулоновского отталкивания. Кулоновская энергия двух осколков с зарядами Z₁и Z₂, находящихся на расстоянии δ, равна

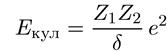. (10.60)

Если считать, что

δ= R₁+R₂,

где R₁, R₂ — радиусы ядер осколков, которые

могут быть вычислены по формуле

R = 1,23 • 10^~13А^1/3 см,

a Z₁ = Z₂ = Z₀/2 ~ 46

(считая, что ядро урана делится пополам), то получим

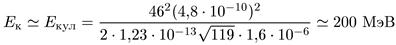
т. е. значение такого же порядка, что и Q_f

3. Образующиеся при делении осколки должны быть β-радиоактивными и могут испускать нейтроны. Причина заключается в том, что, по мере увеличения заряда ядра, отношение числа нейтронов в ядре к числу протонов растет из-за увеличения кулоновской энергии протонов. Поэтому ядра-осколки будут иметь при делении такое же отношение N/Z, как, скажем, у урана, т. е. будут перегружены нейтронами, а подобные ядра испытывают β-распад (ввиду большой перегрузки нейтронами продукты этого распада также β-активны, так что осколки деления дают начало достаточно длинным цепочкам из радиоактивных ядер). Кроме того, часть энергии может уноситься путем непосредственного испускания нейтронов деления или вторичных, т. е. испускаемых из осколков деления, нейтронов. Средняя энергия нейтронов деления составляет около 2 МэВ.

Среднее число нейтронов ν, испускаемых за один акт деления, зависит от массового числа делящегося ядра и растет с ростом Z. Если для ядра ²⁴⁰Рu ν ~ 2,2, то уже для ²⁵²Cf ν ~ 3,8. Так как ²⁵²Cf к тому же достаточно быстро распадается (по отношению к спонтанному делению Т_1/2 = 85 лет; реально его время жизни определяется α-распадом и составляет 2,64 г.), то он является интенсивным источником нейтронов.

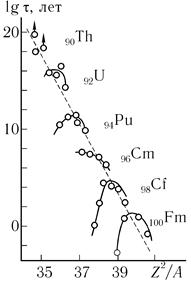
Рис. 10.20

В настоящее время его рассматривают как один самых перспективных радиоактивных источников нейтронов.

Большое энерговыделение и испускание вторичных нейтронов в процессе деления ядер имеют огромное практическое значение. На этом процессе основана работа ядерных реакторов, которые будут рассматриваться в следующей главе.

ГЛАВА 11

Date: 2015-05-19; view: 1065; Нарушение авторских прав