Модели ядра

Атомное ядро представляет собой квантовую систему, состоящую из хотя и большого, но ограниченного числа частиц. Подобная ситуация полностью отлична от той, с которой мы встречались раньше, рассматривая состояния электронов в атомах. В атомах электроны движутся в заданном кулоновском потенциале, в ядре нуклоны движутся в потенциале, который сами же и создают. Фактически здесь мы имеем дело с квантовой задачей многих тел, которая не решена даже для случая трех тел. Поэтому в теории ядра широко

развит модельный подход.

Ядерные модели должны прежде всего описывать свойства основных состояний и спектр возбуждений, являющиеся важнейшей характеристикой любого квантового объекта. Другими словами, ядерные модели должны дать объяснение стабильности ядерного вещества, с помощью нескольких параметров дать возможность вычислить энергию связи как устойчивых, так и неустойчивых (самопроизвольно распадающихся) ядер. Кроме того, они должны правильно описывать типы возбуждений, возможных в ядре.

Рассмотрим подробно капельную модель ядра, которая позволяет правильно вычислить энергии связи ядер (т. е. найти их основное состояние), а также коллективные движения нуклонов, что особенно важно при описании процесса деления атомных ядер. Кроме того, мы качественно обсудим оболочечную модель ядра и причину появления магических чисел нуклонов.

Модель эюидкои капли, формула Ваицзеккера. Результаты измерения радиусов ядер показали, что плотность массы в них приближенно постоянна для различных ядер, т. е. объем ядра V пропорционален числу нуклонов А в нем. Как уже подчеркивалось раньше, этим ядро очень напоминает обычную жидкость, откуда и произошло название модели эюидкой капли, предложенной в 30-х годах независимо К. Вайцзеккером(р.1912г) и Н. Бором. В этой модели ядра рассматриваются как практически несжимаемые заряженные

капли ядерного вещества.

Рассмотрим, каким образом с помощью капельной модели может быть получена формула, выражающая энергию связи (и тем самым массу) ядра через его массовое число А (полное число нуклонов) и заряд Z (число протонов). Число нейтронов N в ядре при этом равно

А - Z. Прежде всего в такую формулу следует включить члены с объемной Е_v, поверхностной E_s и кулоновской Е_к энергиями:

E_v = αA, (10.14)

E_s = -βA^2/3 (10.15)

Е_к = -γZ²/A^1/3 (10.16)

Здесь α, β и γ — некоторые константы, значения которых подбираются так, чтобы модель наилучшим образом описывала экспериментальные данные. Соотношение (10.14) отражает постоянство Е_св/А, следующее соотношение (10.15) — уменьшение энергии связи у поверхностных нуклонов (напомним, что в силу постоянства ядерной плотности объем ядра пропорционален числу нуклонов А, поверхность ос А^2/3, а радиус ос А^1/3), а член (10.16) учитывает кулоновское отталкивание протонов, пропорциональное величине Z² /А^1/3. Указанную зависимость легко понять, если вспомнить, что, например, потенциальная энергия равномерно заряженного шара радиуса R равна (3/5)Z²/R.

Если ограничиться только перечисленными слагаемыми, то окажется, что чем больше нейтронов в ядре, т. е. чем больше величина А при постоянном Z, тем больше Е_св = E_v + E_s + Е_к, и тем стабильнее ядро. Однако действительность оказывается иной: стабильными (устойчивыми) являются далеко не все возможные комбинации из протонов и нейтронов. На координатной плоскости ZN стабильным ядрам соответствует лишь узкая полоска с вполне определенными соотношениями между Z и N (см. рис. 10.3).

Теперь представим себе, что над плоскостью ZN по оси, перпендикулярной ей, отложены величины, обратно пропорциональные временам жизни ядер, т. е. величины, определяющие стабильность этих ядер. Получившуюся поверхность называют долиной стабильности. В самом низу, на ее дне, окажутся стабильные ядра, а вокруг них резко поднимутся горы нестабильных. Чем короче время жизни ядра, тем выше его «гора», с которой он «скатывается» в долину стабильности. В легких ядрах, лежащих на дне долины, число протонов примерно равно числу нейтронов, и этот факт необходимо отразить введением так называемого члена с симметрийной энергией

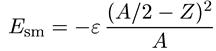
(10.17)

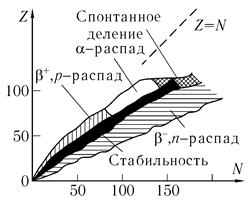
Рис. 10.3

В тяжелых ядрах равновесие N ~ Z нарушается в пользу нейтронов в силу упомянутого

выше свойства суммы Е_v + E_s + Е_к.

Симметрийная энергия возникает вследствие квантовых свойств ядерной материи, а именно, в силу того, что и протоны и нейтроны являются фермионами, т. е. для них справедлив принцип Паули. Это означает, что нуклоны последовательно заполняют дискретные энергетические уровни, образующиеся в потенциальной яме ядра совершенно аналогично тому, как происходит заполнение электронных уровней в атоме. Так как электрический заряд разных нуклонов различен, протоны и нейтроны независимо последовательно заполняют свои энергетические уровни. На рис. 10.4 схематически изображены протонный и нейтронный потенциалы. Из-за наличия у протонов кулоновского взаимодействия глубина потенциальной ямы для них несколько меньше, чем для нейтронов (эта разница обозначена на рисунке как Е_с). Полная энергия ядра минимальна, когда наивысший протонный и нейтронный уровни находятся на одной высоте, примерно на В = 8 МэВ ниже нулевого уровня (эта величина и есть энергия связи нуклонов).

Рис. 10.4 протонный и нейтронный потенциалы

Если, скажем, нейтронов в ядре больше и их наивысший занятый уровень по энергии расположен выше последнего занятого протонного уровня, то ядро оказывается нестабильным и путем β-распада внутриядерного нейтрона n —>> р+е^- + ν* переходит в состояние с меньшей энергией. Аналогично при избытке протонов ядро нестабильно по отношению к позитронному распаду.

Из приведенных аргументов сразу следует вывод: если величины нейтронного и протонного потенциалов одинаковы, как это практически имеет место в легких ядрах, то числа протонов и нейтронов в ядре должны быть одинаковы, что и наблюдается экспериментально. По мере увеличения Z, в силу роста кулоновского отталкивания протонов, глубина их потенциальной ямы уменьшается, а значит, в ядре будет больше нейтронов.

Это свойство ядерной материи наглядно описывается следующей аналогией. Представим, что нейтроны и протоны подобно обычным жидкостям заполняют два сосуда, соединенные между собой снизу трубкой. Жидкости в сосудах всегда находятся на одном уровне. Как только один из сосудов поднимается, что соответствует изменению глубины потенциальной ямы, так жидкость из него сразу же переливается в другой, обеспечивая минимум энергии.

И, наконец, в энергии ядра следует учесть так называемый эффект спаривания. Эксперименты свидетельствуют о наличии дополнительного взаимодействия притяжения, заставляющего два одинаковых нуклона спариваться между собой, образуя состояния с нулевым моментом количества движения. С подобной спиновой зависимостью потенциала взаимодействия мы уже встречались при обсуждении молекулы водорода. Указанное обстоятельство приводит к тому, что наиболее устойчивы четно-четные ядра (ядра с четным числом протонов и четным числом нейтронов), затем идут четно-нечетные

и, наконец, нечетно-нечетные. Причем масса ядер при последовательном изменении заряда Z на единицу меняется не плавно, а скачкообразно. Любой непарный нуклон всегда имеет меньшую энергию связи. Данный экспериментальный факт учитывается слагаемым Еси, таким, что

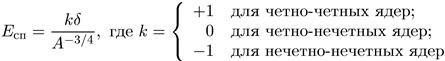
(10.18)

В результате аппроксимирующая функция для энергии связи имеет вид

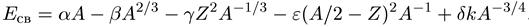. (10.19)

Значения констант, входящих в формулу (10.19), можно найти, подгоняя ее

под экспериментальные данные. Были получены следующие значения коэффициентов (в МэВ):

α = 14,03, β= 13,03, γ = 0,5835, ε= 77,25, S = 34,57. (10.20)

Полуэмпирическая формула (10.19) называется формулой Вайцзеккера.

Ее можно использовать для исследования свойств стабильности неизвестных

искусственных элементов и выяснения характера их распадов.

Следует отметить, что значения констант (10.20) увязаны между собой

процедурой нахождения оптимального описания экспериментальных данных и зависят от этой процедуры. Поэтому в литературе можно встретить значения, немного отличающиеся от приведенных здесь. К тому же некоторые авторы используют иные зависимости последнего члена в (10.19) от А, например, А^~1/3.

Оболочечная модель ядра. Капельная модель не может объяснить особую устойчивость ядер, имеющих некоторые определенные числа нейтронов и протонов. Например, обнаружилось, что такие элементы, как цирконий (50 нейтронов), олово (50 протонов), барий (82 нейтрона), свинец (82 протона и 126 нейтронов) встречаются на Земле чаще, чем соседние с ними элементы периодической системы. Четыре известных радиоактивных семейства заканчиваются стабильными изотопами, содержащими либо 82 протона, либо 126 нейтронов, либо 82 протона и 126 нейтронов. О высокой стабильности ядер ⁴Не (два протона и два нейтрона) и ¹⁶О (восемь протонов и восемь нейтронов) можно судить по их энергии связи, большей, чем соответствующие энергии соседних изотопов (см. рис. 10.1). Кроме приведенных существуют и другие факты, указывающие на то, что ядра, у которых количество нейтронов или протонов совпадает с числами 2, 8, 20, 28, 82, 126, обладают

особыми свойствами. Эти числа, как уже говорилось, назвали магическими, поскольку было неясно, что они отражают.

Тот факт, что в рамках капельной модели невозможно объяснить особые свойства ядер, содержащих магические числа нуклонов, вполне понятен.

В самом деле, если ядро можно рассматривать как жидкую каплю, то его свойства не должны существенно изменяться при добавлении нескольких нуклонов.

Повышенная стабильность ядер с магическими числами нуклонов очень похожа на свойства электронной системы в атомах. Однако задача о структуре энергетических уровней ядра отличается от аналогичной задачи о сложном атоме прежде всего тем, что в атоме имеется центральное тело — ядро, и достаточно хорошим приближением является задача о движении электрона в заданном потенциале. Для ядра сведение задачи многих тел к одночастичной представляется на первый взгляд безнадежным делом, поскольку взаимодействие между нуклонами весьма велико, и отсутствие центрального тела не позволяет решать ее по аналогии с атомом.

Однако квантовые свойства нуклонов накладывают свои особенности на их движение. Впервые на это указали М. Гепперт-Майер(1906-1972) и И. Енсен в 1949 г.

В основном состоянии ядра нейтроны и протоны по одному заполняют самые нижние энергетические состояния. Если внести в систему добавочный нуклон, то он может занять только вышележащий незанятый уровень. Двигаясь в поле ядра, добавочный нуклон, конечно, будет сталкиваться с остальными нуклонами ядра. Однако в большинстве своем такие столкновения не могут привести к изменению состояния ядра, т. е. к передаче импульса, поскольку изменить состояние нуклона можно, только сообщив ему энергию,

достаточную для перехода вверх на одно из незанятых состояний. Поэтому в процессе движения в ядре нуклон практически не меняет своей энергии.

Таким образом, движение каждого нуклона в ядре можно рассматривать как движение в усредненном поле, образованном другими нуклонами, а это означает, что задача о спектре

состояний нуклонов в ядре может быть сведена к одночастичной задаче.

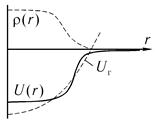
Pis. 10.5 peaлистичный потенциал, воспроизводящий распределение плотности нуклонов в ядре, и его аппроксимация; для сравнения приведено распределение плотности числа нуклонов ρ(r).

Естественно предположить, что усредненное нуклонное поле является центральным, а вследствие короткодействующего характера ядерных сил, форма этого потенциала должна быть похожа на форму распределения плотности нуклонов в ядре. Хорошим приближени-

ем реалистичного ядерного потенциала является потенциал гармонического

осциллятора вида

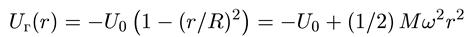. (10.21)

На рис. 10.5 показаны реалистичный потенциал, воспроизводящий распределение плотности нуклонов в ядре, и его аппроксимация; для сравнения приведено распределение плотности числа нуклонов ρ(r).

Энергия трехмерного гармонического осциллятора равна

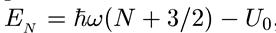, (10.22)

где N = n₁ + n₂ + n_з (n₁, n₂, n_з — целые числа), а U₀ — глубина потенциала. Совокупность близлежащих уровней можно рассматривать как нуклонные «оболочки». В случае трехмерного осциллятора группы уровней с разными N как раз и соответствуют разным оболочкам. Такие уровни сильно вырождены, поскольку одно и то же значение энергии (соответствующее одному и тому же значению N) можно получить, беря различные комбинации чисел их, n₂, n_з. Кратность вырождения N-го уровня S равна числу способов, которыми N может быть представлено в виде суммы трех целых (включая значение 0) положительных чисел. Другими словами, это — число способов, которыми N одинаковых шаров могут быть разложены по трем ящикам, и оно равно

S = (N + l)(N + 2)/2. (10.23)

Отсюда сразу следует, что магическими должны быть числа 2, 8, 20, 40, 70 и т. д. Но, кроме первых трех, в экспериментальных результатах они не встречаются. Правильное «магическое» заполнение оболочек получается, если допустить, что в ядрах существует достаточно сильное спин-орбитальное взаимодействие, сосредоточенное в основном вблизи поверхности ядра, поэтому оно более существенно именно для тяжелых ядер, для которых и получается неверная последовательность магических чисел в простой модели

трехмерного осциллятора.

Возбуэюденные состояния ядер. В результате различных ядерных реакций и ядерных превращений нуклоны могут занимать и энергетически более высоко расположенные состояния. Совокупность уровней возбуждения образует спектр возбуждений атомного ядра. Уровни возбуждения бывают одночастичными (они хорошо описываются оболочечной моделью ядра), двух-, трехчастичными (и т. д.) и коллективными — вращательными, соответствующими вращению ядра как целого (это возможно, конечно, только у несферических ядер), или колебательными, соответствующими колебаниям ядерной плотности или поверхности ядра. Значительное число уровней имеет сложную смешанную природу. Наиболее полное теоретическое описание свойств ядер получается в обобщенной модели ядра, развитой О. Бором(р.1922) и Б. Моттельсоном(р.1926), в которой учитывается влияние коллективного движения нуклонов на параметры одночастичного потенциала.

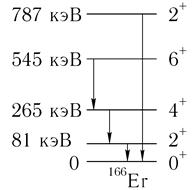
рис. 10.6. спектр низколежащих уровней четно-четного ядра эрбия-166 Ег, у которого вблизи основного состояния наблюдается вращательная полоса положительной четности 2⁺, 4⁺, 6⁺

В качестве примера вращательных состояний на рис. 10.6 приведен спектр низколежащих уровней четно-четного ядра эрбия-166 Ег, у которого вблизи основного состояния наблюдается вращательная полоса положительной четности 2⁺, 4⁺, 6⁺. Отметим, что энергия вращательных уровней (по крайней мере, самых первых) на порядок меньше энергии возбуждения одночастичных, масштаб которой порядка МэВ.

У ядра есть еще одна своеобразная коллективная степень свободы, а именно, колебания всей массы нейтронов относительно всех протонов (дипольные колебания ядра). Поскольку в процессе таких колебаний происходит частичное разделение всех протонов по отношению к нейтронам, они появляются при намного большей энергии, чем колебания поверхности ядра, которые затрагивают лишь несколько поверхностных нуклонов. Характерная энергия таких колебаний, названных гигантским резонансом, лежит в диапазоне 15-20 МэВ. Зависимость частоты гигантского резонанса от А легко оценить. Для любого осциллятора резонансная частота ω₀ определяется жесткостью k и колеблющейся массой m (ω₀= √(k/m). В рассматриваемом нами механизме дипольных

колебаний роль упругой возвращающей силы играет взаимодействие «сдвинутых» нуклонов с ядром. На рис. 10.7 дано схематическое изображение дипольных колебаний ядра, соответствующих гигантскому резонансу.

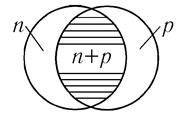
Рис 10.7. схематическое изображение дипольных колебаний ядра, соответствующих гигантскому резонансу

Число «сдвинутых» нуклонов пропорционально поверхности ядра, т. е. R².

Масса колеблющихся нуклонов ~ R³. Тем самым для энергии гигантского

резонанса (частоты) имеем:

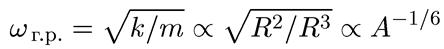(10.24)

Эта зависимость неплохо согласуется с экспериментальными данными.

При энергии возбуждения ~ 5-6 МэВ число уровней в ядрах (особенно в средних и тяжелых) очень велико, а следовательно, мало расстояние между ними. Установить в таких условиях характеристики каждого отдельного уровня и практически невозможно, и не нужно. Целесообразно ввести понятие плотности уровней с данными квантовыми характеристиками, т. е. число уровней, приходящееся на единичный интервал энергии. Именно эта величина обычно входит в формулы, описыващие различные ядерные процессы при сравнительно больших энергиях возбуждения.

Зависимость плотности уровней от энергии описывается с помощью статистической модели ядра, которая рассматривает возбуждение как нагрев нуклонного газа, связывая энергию возбуждения с температурой нагрева ядра. Эта модель основана на применении термодинамических понятий и закономерностей, которые подробно рассматриваются в следующей части.

Температуру ядра можно определить из средней энергии его возбуждения

точно так же, как это делается в термодинамике:

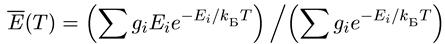, (10.25)

где суммирование производится по всем уровням с энергией E_i с учетом их вырождения (g_i — статистический вес i-го уровня). Функция Е(Т) — зависимость энергии ядра от температуры — при Т = 0 должна иметь, согласно третьему началу термодинамики, нулевую производную (теплоемкость):

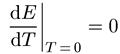. (10.26)

Поэтому разложение Е(Т) в ряд при малых Т должно начинаться с квадратичного члена. Следовательно, при малых температурах можно пренебречь членами более высокого порядка и считать, что

Е = аТ². (10.27)

Энтропия системы S в термодинамике вводится через соотношение

dE = TdS (10.28)

откуда

(10.29)

В то же время по статистическому смыслу энтропия связана с плотностью

состояний системы:

S = lnW(E), (10.30)

т. е. в нашем случае плотность уровней

ρ(Е) = Ce^2√aE. (10.31)

Константы а (параметр плотности уровней) и С можно вычислить из модельных представлений или найти на основе экспериментальных данных. Для нас существенно то, что плотность уровней растет с энергией экспоненциально.

В отличие от основного состояния, возбужденные состояния атомных ядер имеют

конечное время жизни т и в результате переходят в основное (или ниже расположенное) состояние нуклонной системы путем испускания каких-либо частиц. Согласно соотношению неопределенностей это приводит к существованию конечной ширины

уровня Г, такой, что

Гτ ~ ћ. (10.32)

Чем выше энергия возбуждения ядра, тем больше возможностей появляется для снятия этого возбуждения, а, значит, тем меньше т и больше Г. При высоких энергиях возбуждения уровни сближаются настолько, что начинают перекрываться, т. е.

расстояние между уровнями D ~ Г, и спектр становится непрерывным. На основании формулы (10.31) легко получить соотношение между плотностями уровней

при разных энергиях:

(10.33)

Рис. 10.8 спектр возбужденных состояний ядра и то, как он отражается в сечениях ядерных реакций

Параметр плотности уровней а для средних ядер приблизительно равен 10. Поэтому, например, если при нулевой температуре (невозбужденное ядро) расстояние между уровнями D составляет 100 кэВ, то при энергии 8 МэВ, в соответствие с формулой (10.33),

оно падает примерно в 108 раз, т. е. до значения порядка 10~3 эВ.

Схематически спектр возбужденных состояний ядра и то, как он отражается в сечениях ядерных реакций, показаны на рис. 10.8. Как следует из экспериментов, дискретный характер спектра уровней существует и при энергии ядра, превышающей энергию присоединения нуклона (энергию связи).

Это является на первый взгляд странным результатом, поскольку в атомной физике аналогичной области возбуждений (выше энергии ионизации) соответствует непрерывный энергетический спектр. Все дело в том, что, в силу короткодействия ядерных сил, ядерный потенциал скорее похож на прямоугольную яму, и поэтому при приближении энергии к нулю ядерным силам соответствует конечное число связанных уровней (напомним, что в

прямоугольной яме энергия уровня Е_n ос n², тогда как в кулоновском поле она пропорциональна 1/n²).

Date: 2015-05-19; view: 869; Нарушение авторских прав