Энергия двухатомной молекулы

Рассмотрим движения, которые могут происходить внутри молекулы АВ, состоящей из двух атомов Aw. В. Во-первых, внутри молекулы име­ются электроны, которые находятся в непрерывном движении. Кроме этого, атомы А и В могут колебаться относительно центра масс молеку­лы, а также молекула может вращаться вокруг оси, проходящей через центр масс. Каждому из этих видов движения соответствует определен­ное значение энергии. Таким образом, выражение для энергии молекулы Е можно записать так:

E_e + E_v + E_r (22.23)

где Е_е - энергия электронов; E_v - колебательная, или вибрационная энергия молекулы; Е_Т - вращательная, или ротационная энергия.

Представим себе двухатомную молекулу в виде двух частиц, соеди­ненных пружинкой (рис. 22.7). E =

Пусть массы атомов равны m ₁ и m ₂, a жесткость пружинки - с. Разумеется, никаких пружинок в молекуле нет, а есть реальные силы притяжения и отталкивания, действующие между атомами. Взаимодействие атомов характеризуется зависимостью потен­циальной энергии от расстояния между ними. Эту зависимость мож­но описать приближенной формулой (22.1), положив в ней f = 0. Это означает, что молекулу в первом приближении можно рассматривать как гармонический осциллятор.

x ₁ x ₂

Рис. 22.7. Модель двухатомной молекулы

Стационарное движение двух частиц вдоль проходящей через них оси х согласно представлениям квантовой механики будем описывать посред­ством функции

ψ = ψ (x ₁, x ₂),

где x ₁и x ₂ ~ координаты частиц. Эта функция является решением урав­нения Шредингера

в котором оператор Гамильтона 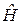Н равен сумме операторов кинетических

энергий частиц

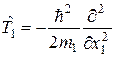
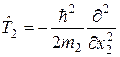
и оператора потенциальной энергии их взаимодействия

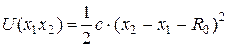
Подробнее уравнение Шредингера для двух частиц можно записать так:

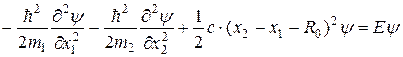
Волновая функция, описывающая движение частиц относительно их центра масс, должна зависеть только от разности координат:

ψ = ψ (ξ) (22.24)

■ где

ξ = x ₂ – x ₁ – R ₀

Подстановка функции ψ = ψ (ξ) в уравнение Шредингера преобразует его к виду

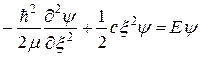(22.25)

- приведенная масса молекулы. Функция (22.24), Являющаяся решени­ем уравнения (22.25), описывает стационарное состояние гармонического осциллятора, частота колебаний которого

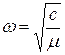
Энергия такого осциллятора принимает значения

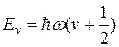, (22.26)

где колебательное квантовое число

v = 0, 1, 2,…

Энергия вращающегося тела зависит от его угловой скорости Ω соглас­но известной формуле

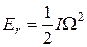, (22.27)

где I - момент инерции тела. Нетрудно доказать, что момент инерции системы двух материальных точек относительно оси, проходящей через центр масс системы, равен

I = μ ,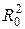

где μ - приведенная масса, R_o~ расстояние между частицами.

Момент импульса тела прямо пропорционален его угловой скорости:

L = IΩ

При помощи этой формулы выражению (22.27) для энергии вращения можно придать вид

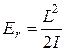. (22.28)

Значения, которые может принимать момент импульса молекулы,

можно найти по формуле

,

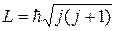где вращательное квантовое число

j = 0, 1, 2,...

Подстановка выражения (22.29) в формулу (22.28) дает

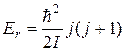
Таким образом, с учетом формул (22.26) и (22.30) для колебательной и вращательной энергий молекулы можно утверждать, что ее энергия (22.23) зависит от квантовых чисел v и j = 0,1,2,3,...

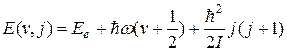(22.31)

Эта формула определяет спектр энергий молекулы и расположение энер­гетических уровней. Причем в силу неравенства

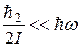
'расстояния" между вращательными уровнями, для которых число v = const, а число j принимает различные значения, меньше "расстояний" между колебательными уровнями, для которых j = 0, а число v и зме­няется. В свою очередь "расстояния" между колебательными уровнями меньше "расстояний" между уровнями энергий электронов. Схема рас­положения уровней энергии молекулы показана на рис. 22.8.

j = 0, 1,2,3,...

j = 0, 1,2,3,...

v = const = 0 j = 0, 1, 2, 3, … v = 2 v = 1 v = 0 E E_e

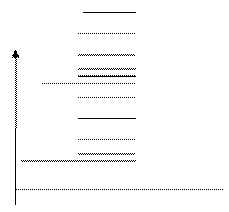
Рис. 22.8. Энергетический спектр молекулы

При переходе молекулы из одного состояния в другое она испуска­ет или поглощает фотон. Спектр частот и электромагнитного излуче­ния молекулы определяется формулой ħω = E ₂ – E ₁, где Е₁ и Е₂ -какие-либо два значения энергии молекулы из ее энергетического спек­тра (22.31).

Date: 2015-05-19; view: 1127; Нарушение авторских прав