
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Химическая связь
|
|
Связь атомов в молекулах называется химической связью. Она почти полностью обусловлена силами электростатического взаимодействия между электронами и ядрами атомов. Однако объяснить это явление можно только при помощи законов квантовой механики. Различают ковалентную и ионную связи атомов в молекулах. Различия между этими типами связи определяются различными пространственными распределениями валентных электронов в молекулах. Химическая связь двух атомов называется ковалентной, если волновая функция, описывающая движение внешнего электрона, такова, что он с равной вероятностью может находиться около любого из этих атомов. В таком случае говорят, что электрон принадлежит сразу двум атомам. Ковалентная связь характерна для молекул, состоящих из одинаковых атомов. Типичный пример ионной связи - связь атомов натрия Na и хлора С1 в молекуле NaCl. В этой молекуле единственный внешний электрон атома натрия переходит к атому хлора. В результате образуются ионы Na+ и С1-, между которыми действуют силы кулоновского притяжения.
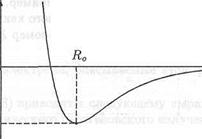
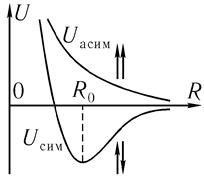
Независимо от того, какой характер имеет связь атомов в молекуле, при больших расстояниях (R > Ro) атомы притягиваются друг к другу, а при малых (R < Ro) они отталкиваются. При этом потенциальная энергия U взаимодействия атомов зависит от расстояния R между ними. Примерный график этой зависимости показан на рис 7.1.
 U
U
| R |
U 0
Рис. 22.1. Зависимость потенциальной энергии U взаимодействия двух атомов от расстояния R между ними
Запишем несколько первых членов разложения функции U = U(R) в ряд Тейлора по степеням R— Ro:
:.
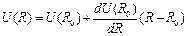 +
+
+ 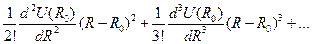
Так как

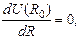
в окрестности точки Ro зависимость U = U(R) потенциальной энергии двух атомов от расстояния между ними можно описать приближенной формулой
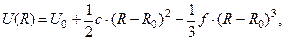 (22.1)
(22.1)
где
U0 = U(R0), c = 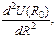 f = -
f = - 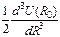
При f = 0 формула (22.1) описывает потенциальную энергию гармонического осциллятора. Система, потенциальная энергия которой зависит от расстояния R согласно формуле (22.1), где f ≠ 0, называется ангармоническим осциллятором.
22.2. Ион молекулы водорода *
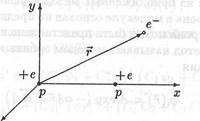
Молекула водорода Н2 состоит из двух атомов водорода. Ион молекулы водорода H2+ образуется при удалении из молекулы водорода одного электрона, т.е. ион Н2+ состоит из трех частиц: двух протонов и одного электрона (рис. 22.2).
|
Рис.22.2.Ион молекулы водорода
Уравнение Шредингера для системы, в которой содержится больше двух частиц, нельзя решить аналитически. При отыскании приближенного решения учитывают тот факт, что массы протона и ядер атомов значительно превышают массу электрона. Поэтому электроны движутся в атомах быстрее ядер. Предполагают что, ядра движутся так медленно, что при любом их расположении система электронов находится в стационарном состоянии.
Стационарное состояние электрона, движущегося в электрическом поле двух протонов, описывается волновой функцией
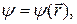
которая является решением уравнения Шредингера
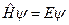 ,
,
где оператор полной энергии электрона
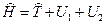 , (22.4)
, (22.4)
где оператор его кинетической энергии
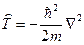
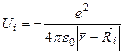
- потенциальная энергия взаимодействия электрона с i -м протоном,
i = 1, 2; 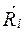 - радиус-вектор этого протона.
- радиус-вектор этого протона.
Волновая функция (22.2) должна удовлетворять условию нормировки
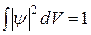 (22.5)
(22.5)
В химии волновые функции электронов в атомах принято называть орбиталями. Один из приближенных методов решения уравнения Шредингера для электрона в молекуле основан на предположении, что волновая функция электрона может быть представлена в виде суммы атомных орбиталей. Этот метод называют методом орбиталей.
Волновая функция
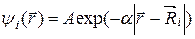
есть волновая функция, описывающая основное состояние электрона, который движется около i -го протона (i = 1, 2) при условии, что другой
протон находится достаточно далеко и не влияет на это движение. Другими словами, функция (22.6) есть орбиталь электрона в атоме водорода. Таким образом, функции ψ 1 и ψ 2 являются решениями уравнений
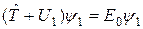
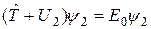 (22.7)
(22.7)
где E 0 = - Rħ - энергия основного состояния электрона в атоме водорода.
Орбитали ψ 1 и ψ 2 - нормированные функции:
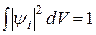
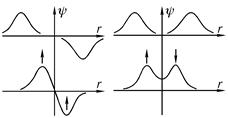
Построим прямоугольную декартову систему координат так, чтобы ось х проходила через протоны, и один из них находился в начале отсчета (рис. 22.2). На рис. 22.3 показаны графики зависимостей от координаты х потенциальных энергий U1 и U2 электрона и его волновых функций (22.6).
■
| - ■::. |
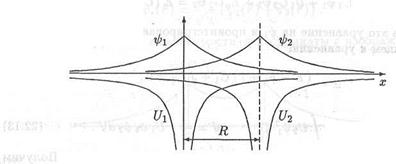
Рис. 22.3. Потенциальные энергии взаимодействия электрона с протонами и его орбитали ψ 1 и ψ 2
Следуя методу орбиталей, представим волновую функцию электрона в ионе молекулы водорода в виде суммы
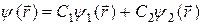 (22.9)
(22.9)
где С1 и С2 - коэффициенты, которые нужно найти. Квадрат модуля функции (22.9)
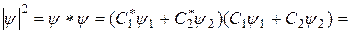
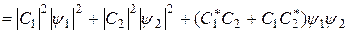
Подставим это выражение в условие нормировки (22.5). Как видно из рис. 22.3, в тех точках пространства, где одна из функций ψ 1 или ψ 2 принимает наибольшие значения, другая функция почти равна нулю. Поэтому так называемый интеграл перекрытия
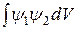
существенно меньше единицы и его можно положить равным нулю. С учетом условий (22.8) придем к равенству
| С 1 |2 + | С 2 |2 = 1
Подставим теперь сумму орбиталей (22.9) в уравнение (22.3). Получим

При помощи равенств (22.7) этому уравнению можно придать вид
E 0 C 1 ψ 1 + U 2 C 1 ψ 1 + U 1 C 2 ψ 2 + E 0 C 2 ψ 2 = E (C 1 ψ 1 +C 2 ψ 2). (22.11)
Умножив это уравнение на ψ 1 и проинтегрировав полученное равенство по 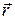 , придем к уравнению
, придем к уравнению
(E – E 0 + I) C 1 + J C 2 = 0 (22.12)
где
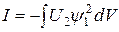
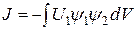 (22.13)
(22.13)
Умножим равенство (22.11) на ψ2 и вновь проинтегрируем по 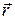 . Получим уравнение
. Получим уравнение
J C 1 + (E – E 0 + I) C 2 = 0
Уравнения (22.12) и (22.14) образуют систему с двумя неизвестными С1 и С2. Эта система имеет нетривиальное решение при условии, что определитель

 E – E 0 + I J
E – E 0 + I J
= 0
J E – E 0 + I
Из этого уравнения найдем возможные значения энергии электрона в ионе молекулы водорода:
E 1, 2 = E 0 – I ± J (22.15)
Как видно из этой формулы, вместо одного значения энергии Ео электрона в атоме водорода, энергия электрона в ионе молекулы водорода может принимать два близких значения E 1 и Е2. Такое явление называется расщеплением энергетического уровня.
Интегралы (22.13) есть положительные монотонно убывающие функции расстояния R между протонами. Они характеризуют влияние, которое оказывает второй протон на движение электрона. Когда расстояние R до этого протона стремится к бесконечности, интегралы (22.13) обращаются в ноль. Из сказанного следует, что значения (22.15) энергии электрона зависят от расстояния R:
E 1 (R) = E 0 – I (R) – J (R) (22.16)
E 2 (R) = E 0 – I (R) + J (R) (22.17)
Пусть энергия электрона в ионе молекулы водорода принимает значение (22.16). Подставив это значение в уравнение (22.12), придем к равенству C 1 = C 2 . Из уравнения (22.10) найдем, что
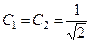 .
.
При этом функция (22.9) примет вид
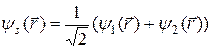 (22.18)
(22.18)
График этой функции в зависимости от координаты а; изображен на рис.22.4.
Ф

 0 R *
0 R *
Рис. 22.4 "Симметричная" волновая функция ψs электрона в ионе молекулы водорода
R

Рис. 22.5. "Антисимметричная" волновая функция ψa электрона в ионе молекулы водорода 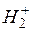
Нетрудно показать, что энергия электрона принимает значение (22.17), когда его состояние описывается " антисимметричной" волновой функцией.
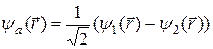
График этой функции в зависимости от координаты х изображен на рис. 22.5.
Полная энергия иона молекулы водорода равна сумме энергии электрона и кулоновской энергии отталкивания протонов:
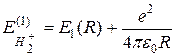 (22.20)
(22.20)
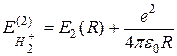 (22.21)
(22.21)
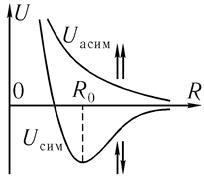
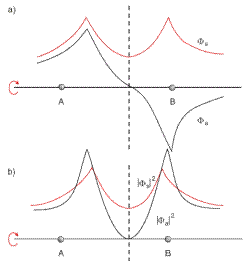
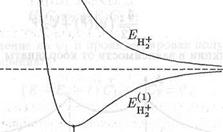
Графики этих функций показаны на рис. 22.6. Как видно из этого рисунка, зависимость (22.20) энергии иона Н2+ от расстояния R между протонами при R > R 0 есть возрастающая функция, т.е. при таких расстояниях протоны притягиваются друг к другу. Это можно объяснить следующим образом.
Соответствующая энергии (22.20) волновая функция (22.18) в пространстве между протонами не равна нулю, т.е. не равна нулю вероятность нахождения электрона в этой области пространства. Электрон при своем движении очень часто оказывается между протонами. При этом силы притяжения протонов к электрону больше сил их отталкивания. Напротив, функция (22.19), соответствующая энергии (22.21), в пространстве между протонами принимает не очень большие значения и даже равна нулю в средней точке (рис. 22.5). Поэтому при таком характере движения электрона силы кулоновского отталкивания протонов больше сил их притяжения к электрону в тех редких случаях, когда он оказывается между ними.
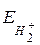

 R
R
■
Рис. 22 6 Энергия иона молекулы водорода H2+
как функция расстояния R между протонами
Молекула водорода находится в состоянии с наименьшей энергией при условии, что движение обоих ее электронов описывается "симметричной" волновой функцией (22.18). При этом спины электронов в силу принципа Паули должны быть направлены в противоположные стороны. В таком случае оба электрона осуществляют ковалентную связь атомов водорода в молекуле Н2, а ее энергия равна сумме энергий электронов и энергии взаимодействия протонов:
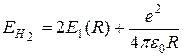 (22.22)
(22.22)
Date: 2015-05-19; view: 736; Нарушение авторских прав