Вероятность. Представим себе физическую систему, возможные состояния которой образуют счетное множество, т.е

Представим себе физическую систему, возможные состояния которой образуют счетное множество, т.е. каждому состоянию можно приписать некоторый номер n = 1, 2, 3,... В физике такие системы называют "кван­товыми". Под влиянием каких-либо внешних воздействий или самопроизвольно (спонтанно) квантовая система может за очень короткое время перейти из одного состояния в другое. Такой "скачок" называют кванто­вым переходом. Будем наблюдать за этой системой в течение достаточно длительного времени τ. За это время система, совершит много переходов из одного состояния в другое и в каждом состоянии она побывает не­сколько раз. Пусть t_n - суммарное время, в течение которого система находилась в n-ом состоянии. Очевидно, что

∑_n t_n= τ

Предел отношения времени t_n пребывания системы в n-ом состоянии ко времени наблюдения τ

W_n = lim _{τ ->∞}(t_n/ τ)

называется вероятностью того, что в некоторый произвольный момент времени система будет находиться в n-ом состоянии. Вычислим сумму

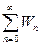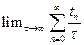= = = 1.

Таким образом, придем к равенству

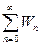=1 (16.32)

которое называется условием нормировки вероятности.

Пусть ε_п - энергия системы в состоянии под номером п. Энергия си­стемы ε(t) в произвольный момент времени t принимает одно из возмож­ных значений ε₀, ε₁ ε₂, Среднее значение энергии системы за время от некоторого t₀ до t_o + τ по определению можно вычислить посредством формулы

= =

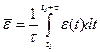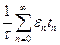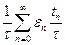
Для достаточно больших промежутков времени τ будем иметь

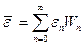(16.33)

Вывод формулы Планка

Теперь найдем спектральную плотность энергии равновесного тепло­вого излучения и освещенность на основе гипотезы Планка о том, что электромагнитное излучение есть совокупность фотонов. Энергия ε од­ного фотона и частота ω излучения связаны формулой

ε = 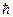ω. (16.34)

Рассмотрим некоторую квантовую физическую систему, находящуюся в состоянии термодинамического равновесия при температуре Т. Аме­риканский физик-теоретик Дж. Гиббс (1839 - 1903) предложил закон, согласно которому вероятность W_n того, что равновесная система в про­извольный момент времени окажется в микросостоянии под номером n, определяется формулой

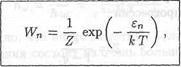
где ε_п ~ энергия системы в состоянии под номером n; k - постоянная Больцмана; Z - величина, не зависящая от номера n состояния. По закону Гиббса чем больше энергия ε_п системы в n-ом состоянии, тем меньше вероятность того, что система в произвольный момент времени окажется именно в этом состоянии.

Подстановка выражения (16.35) в условие нормировки (16.32) приво­дит к формуле

Z=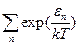

Это выражение называется статистической суммой.

Применим распределение Гиббса для описания состояния равновесно­го электромагнитного излучения в полости, температура стенок которой поддерживается постоянной. При этом будем рассматривать электромаг­нитное излучение как совокупность фотонов. Если одна стоячая волна частоты ω состоит из п фотонов, то ее энергия будет

ε_n =n ε = n 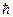ω. (16.37)

В этом случае статистическая сумма (16.36) принимает

Z=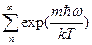

Эту сумму более подробно можно записать как

Z= 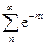=1+e^-x + e^-2x + …

где

x =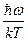

Нетрудно видеть, что эта сумма есть сумма бесконечного числа членов убывающей геометрической прогрессии, знаменатель которой

q=e^-x

Используя известную формулу для суммы членов бесконечной убываю­щей геометрической прогрессии

Z=1/(1-q)

найдем статистическую сумму

Z = 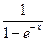(16.39)

Теперь найдем среднюю энергию ε одной стоячей волны. Подстановка выражений (16.35) и (16.37) в формулу (16.33) дает

=

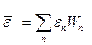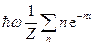
При помощи равенства (16.38) нетрудно убедиться в справедливости тождества

= =

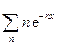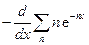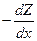
С учетом этого тождества можно записать следующее выражение:

=

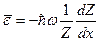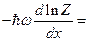
Продифференцируем по х функцию Z = Z(x), определяемую формулой (16.39). После несложных преобразований придем к формуле

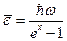(16.40)

Заметим, что для низких частот величина x =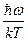

может быть суще­ственно меньше единицы: x << 1. При этом будет справедливо равенство

e^x ≈1+x

используя которое нетрудно доказать, что

ε≈kТ при 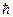ω <<kТ.

Таким образом, полученная на основе квантовых представлений форму­ла остаточно низка.

Среднее число фотонов в волдля средней энергии волны переходит в классическую формулу, если частота волны дне с частотой ω можно найти, разделив энергию волны на энергию одного фотона:

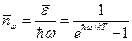(16.41)

Из этой формулы видно, что низкочастотные волны равновесного элек­тромагнитного излучения состоят из очень большого числа фотонов. С увеличением частоты ω среднее число фотонов в волне стремится к ну­лю.

Умножив среднюю энергию ε одной волны на число dN_ω волн в объеме V с частотами в интервале (ω, ω + dω), найдем энергию этих волн (16.29):

w(ω,T)Vdω = εdN_ω.

Подставив в это равенство выражения (16.28) и (16.40), найдем, что

w(ω,T) = 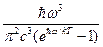(16.42)

Из соотношения (16.26) найдем, что спектральная освещенность Е(ω,Т) определяется формулой (16.43)

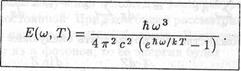
Date: 2015-05-19; view: 558; Нарушение авторских прав