Освещенность поверхности изотропным излучением

Найдем зависимость между плотностью энергии w изотропного излу­чения и освещенностью Е какой-либо поверхности таким излучением.

Рассмотрим сначала плоскую электромагнитную волну, плотность энергии которой равна w, а интенсивность - I. Построим воображае­мый прямой цилиндр, образующая которого совпадает с направлением распространения волны (рис. 16.2). Пусть S - площадь основания этого цилиндра, а его длина равна cdt, т.е. расстоянию, которое преодолева­ет электромагнитная волна за время dt. По определению интенсивность равна среднему по времени значению энергии, которую переносит вол­на за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. В соответствии с этим определе­нием, энергия излучения, выходящего из цилиндра за время dt, равна

W=IS dt.

С другой стороны, эта энергия принадлежит излучению, которое заполняло объем цилиндра, и, переместившись на расстояние с dt, вышло из него в течение времени dt. Энергия излучения, заполняющего некоторую

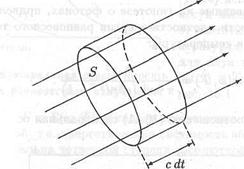
Рис. 16.2. К выводу формулы I = cw

область пространства, равна произведению плотности энергии w на объем этой области. В рассматриваемом случае энергия излучения внутри цилиндра будет

W = wScdt.

Приравняем эти два выражения для энергии. Получим формулу

I = cw, (16.20)

связывающую плотность энергии и интенсивность плоской электромаг­нитной волны.

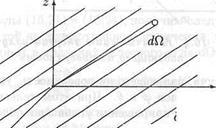
Рассмотрим теперь изотропное электромагнитное излучение, заполня­ющее небольшой объем пространства V. Это излучение можно рассма­тривать как совокупность плоских электромагнитных волн, распростра­няющихся во всевозможных направлениях. Выделим при помощи "уз­кого" конуса часть волн, направления распространения которых лежат внутри этого конуса (рис. 16.3). Если телесный угол dΩ конуса достаточ­но мал, то выделенные волны образуют почти плоскую волну, интенсив­ность dI которой согласно формуле (16.20) пропорциональна плотности энергии dw:

dI = cdw.

х c y

Рис. 16.3. Волны изотропного излучения, которые распространяются вдоль лучей, лежащих внутри "узкого" конуса, образуют почти плос­кую волну

Плотность энергии w изотропного излучения в рассматриваемом объ­еме принадлежит волнам всех направлений, т.е. соответствует полному телесному углу 4π. Для изотропного излучения его энергия распределена равномерно по всем направлениям. Поэтому

dw= 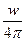dΩ

.

При этом интенсивность излучения, направления распространения кото­рого лежат внутри конуса с телесным углом dΩ, будет

dI= 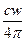dΩ, (16.21)

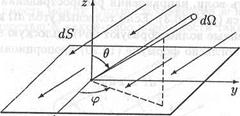
Пусть на плоскую поверхность площадью dS падает изотропное излу­чение. Достаточно "узкий" конус выделяет в этом излучении часть волн, направления распространения которых почти совпадают (рис. 16.4). Эти волны образуют почти плоскую волну. Вследствие этого, энергия, кото­рую они сообщают поверхности за время dt, будет равна произведению их интенсивности dI на площадь dS cos θ поперечного сечения пучка рас­сматриваемых лучей и на время dt:

dW'_nad = dI dS cos θ dt,

где θ - угол падения волн на поверхность, т.е. угол между направлением распространения волн и нормалью к поверхности.

Рис. 16.4. К вычислению энергии излучения, падающего на поверхность

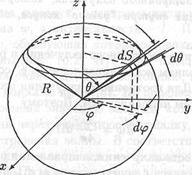
Направление луча, падающего на поверхность, удобно задать при по­мощи сферических уголов φ и θ. При этом телесный угол dΩ можно выразить через угол θ и приращения углов dφ и dθ. Для этого построим сферу произвольного радиуса R (рис. 16.5).

Рис. 16.5. К вычислению телесного угла dΩ,

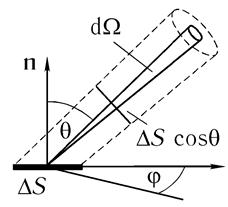
"Вырежем" из поверхности сферы небольшую часть площадью dS_cf. Телесный угол dΩ, под которым видна эта часть поверхности сферы из ее центра, по определению равен отношению ее площади к квадрату ра­диуса сферы:

dΩ = dS_cf/R² (16.23)

Два конуса с углами раствора θ и θ+dθ вырезают из сферы часть, называ­емую шаровым поясом. Площадь пояса равна произведению его ширины R dθ на длину 2π R sin θ:

dS _{шар.пояс} = 2π Rsinθdθ.

Две плоскости, проходящие через ось z и образующие с осью z углы φ и φ + dφ, вырезают из шарового пояса небольшую часть, площадь которой

dS_cf = dS_tuap.noяc /2π = R² sin θdθdφ.

Таким образом, формула (16.23) приводит к выражению

dΩ = sin θdθdφ. (16.24)

Используя формулы (16.21) и (16.24), получим следующее выражение для энергии (16.22) той части изотропного излучения, которая падает на площадь dS за время dt в пределах телесного угла dΩ:

dW'_nad = (cw/4π)

Так как для падающих на поверхность dS лучей угол θ изменяется в пределах от 0 до π/2, а угол φ - от 0 до 2π, энергия излучения, упавшего на эту поверхность из полупространства (т.е. из телесного угла 2π) за время dt, будет

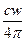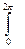dW'_nad = dI= dS dt dφ 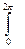cos θ sin θdθ

Из этого равенства с учетом определения освещенности

dW_nad = Е dS dt

следует, что освещенность поверхности изотропным излучением связана с плотностью энергии этого излучения соотношением

E=(1/4)cw

Аналогичное соотношение справедливо для спектральных величин

(16.26)

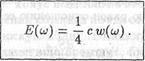
Date: 2015-05-19; view: 751; Нарушение авторских прав