Электромагнитное излучение в полости твердого тела

Рассмотрим электромагнитное излучение, заключенное в полости вну­три некоторого тела. Если температура тела, поддерживается постоян­ной, то со временем установится тепловое равновесие между излучением и стенками полости. В силу закона Кирхгофа свойства и характери­стики равновесного теплового излучения не зависят от формы и хими­ческого состава тел, с которыми оно взаимодействует. Поэтому будем для простоты считать, что стенки полости имеют форму прямоугольно­го параллелепипеда и полностью отражают падающее на них излучение. Направим координатные оси вдоль ребер параллелепипеда, длины кото­рых обозначим а, b, с (рис. 16.6).

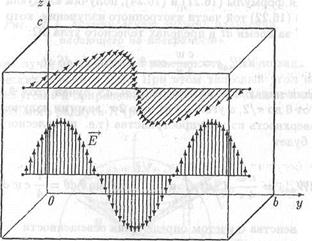
Рис. 16.6. Стоячие электромагнитные волны внутри прямоугольной полости с идеально отражающими стенками

При наложении электромагнитных волн, бегущих навстречу друг дру­гу, образуются стоячие волны. Так как по предположению стенки полости полностью отражают падающее на них излучение, напряженность электрического поля на поверхности полости будет равна нулю. В таком случае функции, описывающие стоячие волны внутри параллелепипеда будут иметь наиболее простой вид. Так, например, волны, распростра­няющиеся вдоль оси у, образуют стоячие волны

E_x(t, у) =А ₁ sin(k_y у) cos(w t + a₁),

Е_у=0

E_z(t, у) = А₂ sin(k_y у) cos(w t + a₂)

где Е_х, Е_у и Е_z - проекции на оси координат вектора Е напряженности электрического поля; А₁ и А₂ ~ амплитуды волн; к_у - волновое число;

а₁ и а₂ - начальные фазы. Вектор Е, определяемый этими формулами, обращается в ноль при у = 0, т.е. на одной из сторон параллелепипеда. Он должен быть равен нулю также и на противоположной его стороне при

у = b:

E (t, b)=0.

Это условие выполняется, если волновое число

k_y = (π/b)п_у

где п_у - целое число. В силу произвольности начальных фаз a₁ и а₂ равные по величине и противоположные по знаку волновые числа к_у характеризуют одну и ту же стоячую волну. Поэтому удобно положить

п_у = 1,2,3,...

Для волн, бегущих вдоль координатных осей х и z, волновые числа при­нимают значения

k_x = (π/b)п_x, k_z = (π/b)п_z

п_x = 1,2,3,..., п_z = 1,2,3,...

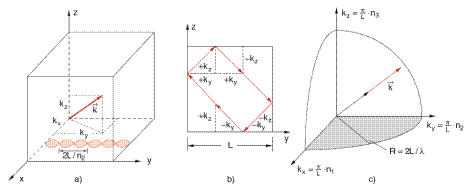
Из полученных формул следует, что стоячие волны, возникающие вну­три параллелепипеда с идеально отражающими стенками, характеризу­ются волновыми векторами

k{ π п_x /b, π п_y /b, π п_z /b}

При этом одному вектору k соответствуют две стоячие волны с различ­ными взаимно перпендикулярными направлениями векторов Е.

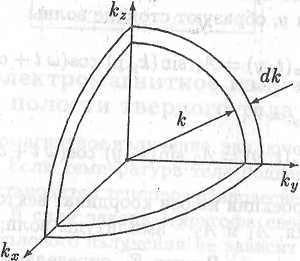
Рис. 16.7. К вычислению числа dN_k волн в прямоугольной полости

Найдем число dN_k стоячих волн, для которых волновые числа (т.е. модули волновых векторов к) лежат в интервале (к, к + dk). Для это­го построим прямоугольную систему координат, на осях которой будем откладывать значения проекций к_х, к_у, к_z волнового вектора к. Каждой стоячей волне будет соответствовать в этом пространстве точка с коор­динатами

(π п_x /a, π п_y /b, π п_z /c)

Все эти точки располагаются в первом октанте пространства и образу­ют прямоугольную "кристаллическую решетку". Объем элементарной ячейки этой решетки равен π³/аbс. Следовательно, концентрация то­чек, являющихся узлами решетки, будет равна abc/π³. Волнам, для которых волновые числа лежат в интервале (к, к + dk), соответствуют точки, лежащие внутри сферического слоя радиуса к и толщины dk (рис. 16.7). Число этих точек равно произведению их концентрации на объем 1/8 части слоя. Так как каждому волновому вектору к соответствуют две стоячие волны с различными поляризациями (направлениями колебаний) вектора Е, то число волн будет вдвое больше числа точек:

dN_k = 2 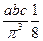4πk²dk = 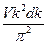, (16.27)

где V — abc - объем параллелепипеда.

Волновое число связано с частотой волны соотношением

k=ω/c

где с - скорость света. При помощи этого соотношения найдем число dN_ω волн в объеме V с частотами в интервале (ω, ω + dω):

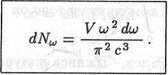
dN_ω = 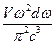(16.28)

16.6. Формула Рэлея – Джинса

Равновесное тепловое излучение является изотропным. Поэтому спра­ведливо соотношение (16.26). Спектральную плотность энергии w = w(ω, T) можно найти следующим образом. Пусть известна средняя энергия ε одной стоячей электромагнитной волны в объеме V, частота которой равна ω. При этом энергия (16.8) волн, частоты которых лежат в интервале (ω, ω+dω), будет равна произведению средней энергии одной волны на число волн:

w(ω, T)Vdω = εdN_ω. (16.29)

Будем рассматривать стоячую электромагнитную волну как некото­рый абстрактный гармонический осциллятор, средняя энергия которого, как известно, равна

ε=kT (16.30)

где к - постоянная Больцмана, Т - абсолютная температура. Подставим это выражение и выражение (16.28) в равенство (16.29). Получим следу­ющую зависимость плотности энергии равновесного теплового излучения от частоты и температуры:

w(ω, T) = кТω²/(π²c)

По формуле (16.26) найдем, что зависимость спектральной освещенности от частоты и температуры описывается формулой

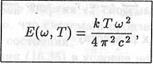
(16.31)

которая называется формулой Рэлея - Джинса. Эта формула не согла­суется с результатами экспериментов и приводит к абсурдному выводу, что энергия равновесного теплового излучения всех частот, падающего за единицу времени на единицу площади какой-либо поверхности беско­нечно велика:

∫₀^∞ Е(ω, Т) dw = оо.

Это следствие формулы Рэлея - Джинса получило название "ультрафи­олетовая катастрофа".

Date: 2015-05-19; view: 1037; Нарушение авторских прав