Визначення взаємозв’язку між ціною і попитом

Для оцінки взаємозв’язку між ціною і попитом на свій новий товар (рівнем його збуту) фірма протягом декількох місяців проводила пробний маркетинг цього товару при різних значеннях ціни.

Результати дослідження ринку, переведені на обсяг річного збуту товару, видаються студентам для подальшого проведення на їх основі статистичного аналізу. Якщо зобразити кожну пару спостережень у системі координат, де величина попиту відкладається на осі у, а ціна - на осі х, то отримаємо кореляційне поле точок.

Рис. 1. Кореляційне поле точок

Завданням студентів є складання рівняння регресії, що встановлює взаємозв’язок між досліджуваними параметрами: ціною та обсягом попиту, що у даному випадку дорівнює рівню фактичного збуту. Оскільки зв’язок між ними близький до лінійного, то рівняння регресії буде мати вигляд:

,

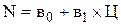де N – теоретичне значення обсягу збуту при відповідній ціні.

На підставі гіпотези про лінійність зв’язку через кореляційне поле точок необхідно провести пряму таким чином, щоб сума квадратів відхилень теоретичних значень від фактичних була мінімальна. В цьому полягає суть методу найменших квадратів. Це означає, що розрахункові значення максимально наближені до фактичних, що є гарантією достовірності моделі.

Використовуючи метод найменших квадратів для обчислення в₀ та в₁ слід розв’язати систему нормальних рівнянь:

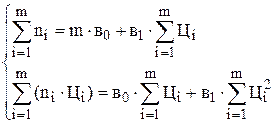
де m – кількість замірів у проведеному дослідженні.

Щоб розв’язати цю систему, треба помножити перше рівняння на:

,

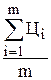та відняти друге рівняння від першого або використати інші методи розв’язування систем рівнянь.

Проміжні дані для розрахунку доцільно показати у вигляді таблиці 1.

Таблиця 1

Проміжні розрахунки

Заміри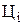
…
…
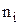
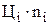
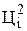
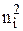
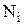
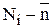
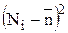
m
Сума	å	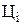å	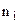å	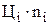å	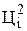å	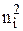å	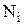–	å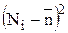

Після розв’язання системи рівнянь, визначення коефіцієнтів в₀ та в₁ та складання рівняння регресії будують графік залежності N від Ц. Приклад графіку функції N=f(Ц) наведений на рис. 2.

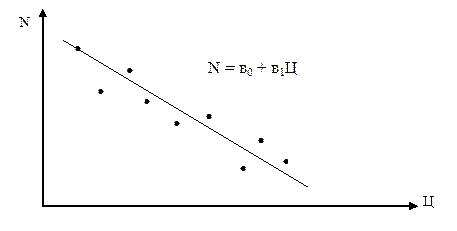
Рис. 2. Залежність попиту від ціни

Студентам слід будувати такий графік у обраному масштабі.

Далі визначають щільність зв’язку між цими величинами, для чого обчислюють коефіцієнт детермінації.

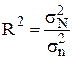
де 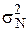– факторна дисперсія, ;

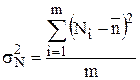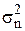– загальна дисперсія,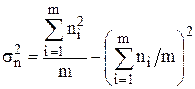

Коефіцієнт детермінації характеризує тісноту зв’язку між даними величинами. Він має додатне значення і знаходиться в межах [0;1]. Залежно від значень роблять наступні висновки:

- якщо , то зв’язок між ціною і попитом слабкий;

- якщо 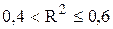, то зв’язок між ціною і попитом відчутний;

- якщо 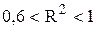, то зв’язок між ціною і попитом щільний.

Використовувати рівняння регресії для подальших досліджень можна при умові щільного зв’язку.

Date: 2015-04-23; view: 679; Нарушение авторских прав