Спин-орбитальное взаимодействие

Электрическое поле не действует на спиновый магнитный момент неподвижного заряда. При движении частицы в электрическом поле появляется магнитное поле в ее собственной системе отсчета за счет преобразования Лоренца. Это поле взаимодействует со спиновым магнитным моментом. Уровень энергии электрона расщепляется, возникают состояния со спином, направленным по- и против магнитного поля. Эффект называется спин-орбитальным взаимодействием (СОВ). Степень расщепления уровня линейно зависит от электрического поля и импульса частицы. СОВ позволяет изменять и контролировать спиновое состояние электрическим полем, которое можно изменять гораздо быстрее магнитного поля потому, что для электрического поля отсутствует явление электромагнитной индукции.

Собственное электрическое поле существует в узкозонном полупроводнике из-за несимметричного распределения зарядов в потенциальной яме, или благодаря примесям и дефектам. СОВ в гетероструктуре 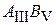с двухмерным газом носителей тока исследовал Эммануил Иосифович Рашба в 1960 г. Большие по сравнению с металлом времена и длины фазовой когерентности и спиновой релаксации в полупроводниках, достигающих ~1 нс и ~100 мкм, малый размер устройств наноэлектроники, баллистическое движение зарядов приводят к интерференции спиновых токов. При низкой концентрации можно пренебречь взаимным влиянием зарядов и использовать одноэлектронное приближение. Гамильтониан заряда записывается в приближении эффективной массы. Получаемые результаты применяются в спинтронике, использующей для преобразования и контроля информации не только заряд, но и спин электрона. На основе СОВ созданы источники спин-поляризованного тока из немагнитных полупроводников.

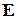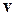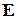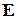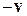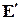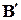Гамильтониан спин-орбитального взаимодействия. В лабораторной системе отсчета имеется однородное электрическое поле . Электрон со скоростью движется перпендикулярно , как показано на рис. a. В собственной системе отсчета электрона источники поля , показанные на рис. а, двигаются со скоростью и создают электрическое и магнитное поля и , показанные на рис. б. Для полей используем преобразование Лоренца

, , , ,

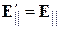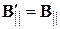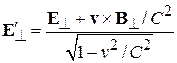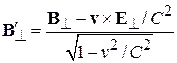где знаки и 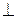обозначают продольные и поперечные к 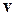составляющие полей.

а б

Электрон в лабораторной (а) и

в собственной (б) системах отсчета

При 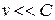в рассматриваемом случае 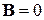, 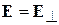получаем

,

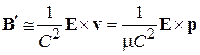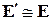, (8.38)

где μ – эффективная масса. Возникающее магнитное поле направлено перпендикулярно электрическому полю и скорости заряда, и удовлетворяет правилу правой руки.

Поле 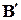действует на спиновый магнитный момент электрона

,

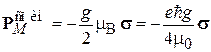где 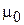– масса покоя электрона. Энергия взаимодействия (8.2)

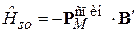
уменьшается в два раза из-за прецессии спина, в результате гамильтониан СОВ электрона

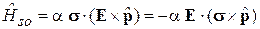, (8.39)

где

.

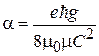Строгий вывод (8.39) основан на разложении квантового релятивистского уравнения Дирака для электрона по степеням 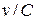до второго порядка.

Для гетероструктур 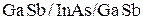, , 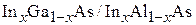Bi на Ag(111) получено

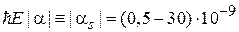эВ·см.

Гамильтониан электрона с зарядом 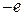, спиновым магнитным моментом 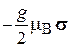в электрическом поле 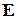, в магнитном поле 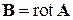, в потенциальной яме с энергией V с учетом (8.39) и 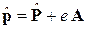получает вид

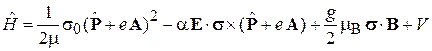, (8.40)

где

.

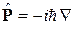При движении в плоскости 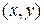в поле 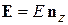из (8.40) находим

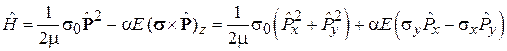. (8.41)

Полевой спиновый транзистор на основе гетероструктуры 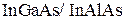показан на рис. а. В 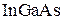около границы с 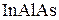в плоскости 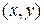существует потенциальная яма 2, показанная серым цветом на рис. а, с двухмерным электронным газом. Из-за несимметричности гетероструктуры по оси z создается электрическое поле со средним значением 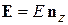. Около слоя 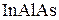расположен затвор 3, его потенциалом можно регулировать конфигурацию ямы, концентрацию электронов и величину электрического поля. Контакты 1 и 4 создают разность потенциалов, слабо тянущую электроны. Электрон в яме с импульсом 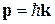и волновым числом 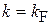движется в плоскости 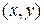, как показано на рис. б. Магнитное поле 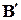расположено в плоскости 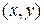. Получим состояния электрона с учетом СОВ путем решения стационарного уравнения Шредингера.

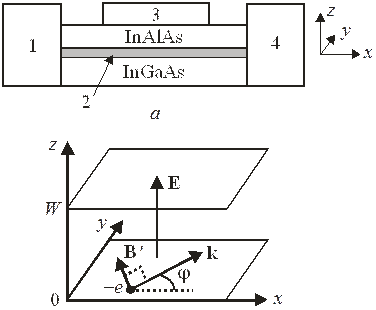
б

Используем (8.41)

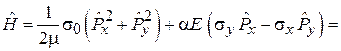
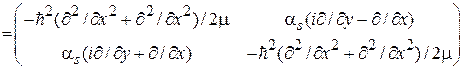, (8.44)

где

.

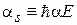Импульс 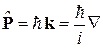коммутирует с гамильтонианом , поэтому решение уравнения Шредингера

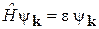
ищем в виде плоской волны с волновым вектором k, направленным под углом φ к оси x:

,

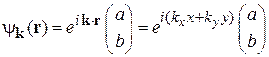где

; ;

; ;

;

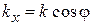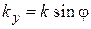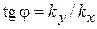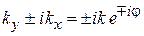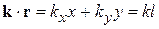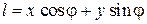– проекция вектора 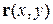на направление k. Подстановка 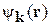в уравнение дает

.

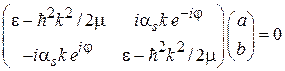Определитель матрицы приравниваем нулю и получаем два решения для зависимости энергии электрона от волнового числа – закон дисперсии

,

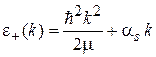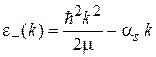. (8.45)

Функции показаны на рисунке, где

; ,

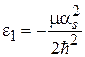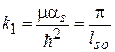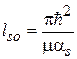– длина спиновой прецессии. Сплошной линией показаны участки с положительной групповой скоростью

.

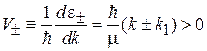Пунктирная линия соответствует участкам с отрицательной скоростью.

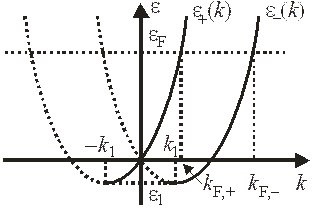
В обозначении энергии состояний знак 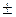показывает знак проекции спина на направление поля 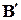при 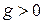. Спиновое расщепление

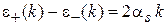
линейно по импульсу и электрическому полю. Из уравнения находим 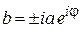, тогда

,

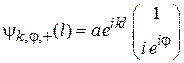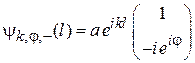. (8.46)

Состояния взаимно ортогональны

.

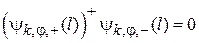Поле 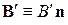направлено под углом 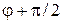к оси x. Оператор проекции спина на направление поля n получаем заменой , 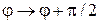в (П.11.6)

.

Выполняется

,

.

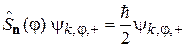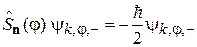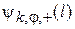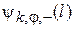Следовательно, состояния и являются собственными функциями оператора проекции спина на направление 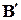с проекциям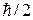и и 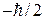. СОВ снимает вырождение энергии по проекциям спина. Если 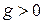, то в основном состоянии с энергией 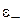спин направлен против поля 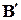, магнитный момент – по полю. В неосновном состоянии с энергией 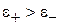указанные направления обратные. Каждому направлению импульса частицы 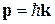соответствует свое направление поля 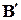и спина в основном состоянии. При обращении движения электрона направление его спина меняется на противоположное. Электроны со спинов вверх движутся в одну сторону, а со спином вниз – в другую сторону.

При низкой температуре энергия электрона равна энергии Ферми при любом направлении спина. Из (8.45) получаем уравнение для верхних границ подзон с противоположными проекциями спина

,

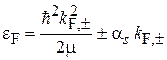откуда

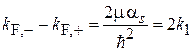. (8.48)

Согласно (8.47) и (8.48) плотность тока спина 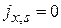, поскольку различие скоростей с разными проекциями спина компенсируется влиянием СОВ.

Пройдя путь l, состояния с противоположными проекциями спина набирают разность фаз

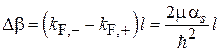, (8.49)

не зависящую от энергии Ферми. Возникает суперпозиция состояний (8.46)

.

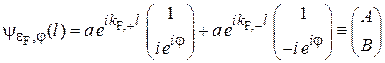Вероятности обнаружить спин вдоль или против оси z равны

,

.

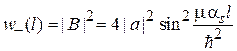Вариация напряжения на затворе гетероструктуры изменяет 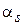и вероятность обнаружения выходящего электрона с определенной проекцией спина. Полевой спиновый транзистор, работающий на этом принципе и использующий на входе и на выходе гетероструктуры магнитные контакты, выполняющие роль поляризатора и анализатора, предложили S. Datta и B. Das в 1990 г.

Топологические изоляторы. В поверхностном слое диэлектрика существует множество поверхностных состояний в запрещенной зоне – уровни Тамма. При достаточной плотности таких состояний валентная зона смыкается с зоной проводимости и образуется поверхностное металлическое состояние. Носителями тока являются валентные электроны, перескакивающие от одного атома к соседнему атому. Однако возбужденный внешним электрическим полем поверхностный ток быстро затухает из-за рассеяния на дефектах и неровностях кристалла, на тепловых флуктуациях. В результате диэлектрик не проводит ток и является изолятором.

При большом заряде ядра валентные электроны атома, образующие поверхностный ток, двигаются в сильном электрическом поле, перпендикулярном поверхности диэлектрика, и подвергаются спин-орбитальному взаимодействию. В собственной системе отсчета электрона магнитное поле параллельно поверхности диэлектрика. Поверхностный ток получает определенное направление спина, параллельное поверхности диэлектрика. У тока противоположного направления спин ориентирован в обратную сторону. При рассеянии изменяется направление движения заряда, что требует поворота спина. Однако передача момента импульса отсутствует, и поэтому рассеяния не происходит. Диэлектрики с такими свойствами – (Hg,Cd)Te, BiSb и ряд других были обнаружены в 2008 г. Они являются изоляторами в своем объеме и очень хорошими проводниками в поверхностном слое толщиной ~ 6,3 нм, и называются топологическими изоляторами. Их двухмерный ток не рассеивается на неоднородностях кристалла, тепловых флуктуациях, электромагнитном шуме, т. е. является сверхпроводящим током. Поэтому другое название таких материалов – топологические сверхпроводники. Потенциалом наружного затвора можно изменять концентрацию носителей тока и тип проводимости от электронной до дырочной.

Если в топологическом изоляторе течет ток одного направления, то все спины и их магнитные моменты выстроены параллельно, и возникает сильная намагниченность. Другой замечательной особенностью топологического изолятора является обращение в нуль эффективной массы электрона проводимости. В результате уменьшается внешнее поле, необходимое для управления электронным устройством, и сокращается время срабатывания устройства. Топологические изоляторы являются новыми перспективными материалами в спинтронике и в устройствах квантовой информатики.

Date: 2015-05-19; view: 932; Нарушение авторских прав