Зависящее от времени возмущение

Зависящее от времени возмущение 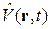, действующее при 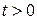, в первом порядке не изменяет уровней стационарной невырожденной системы, но вызывает переходы системы между уровнями. Получим вероятности переходов.

Невозмущенные состояния cтационарной системы с дискретным спектром

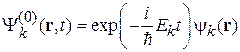
удовлетворяют уравнениям

, ,

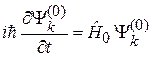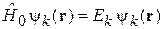ортонормированны

,

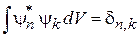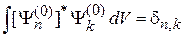
и образуют полный базис 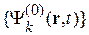. Стационарное состояние с неопределенной энергией разлагается по этому базису

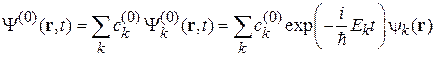(6.30)

и удовлетворяет уравнению Шредингера

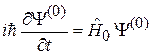. (6.31)

Вероятность обнаружения системы на уровне 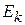равна

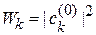. (6.32)

Возмущенное состояние 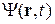удовлетворяет уравнению

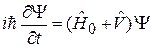(6.33)

и разлагается по базису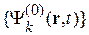

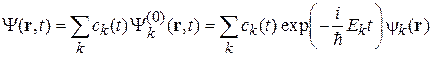(6.34)

с зависящими от времени коэффициентами. Для их нахождения подставляем (6.34) в (6.33) и учитываем (6.31)

.

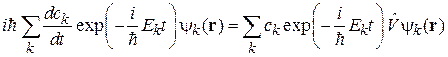Проектируем уравнение на 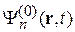, умножая его слева на 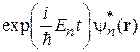и интегрируя по объему. С учетом 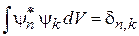получаем уравнение для коэффициентов

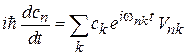, (6.35)

где 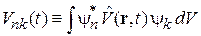– матричный элемент возмущения;

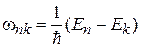(6.36)

– боровская частота перехода между уровнями k и n.

Первый порядок теории возмущений. Коэффициенты ищем в виде

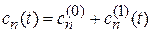, (6.37)

где 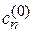– коэффициенты невозмущенного разложения (6.30); 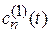– поправка, вызванная возмущением. Подставляем (6.37) в (6.35) и ограничиваемся первым порядком возмущения

.

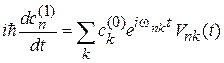Интегрирование по t дает

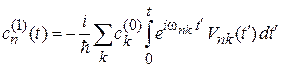. (6.38)

Учтено, что возмущение начинает действовать при 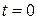и .

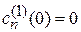Коэффициент перехода между состояниями. Пусть при 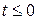система находилась в состоянии m, тогда 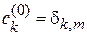и (6.37) дает

,

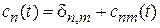где 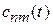– коэффициент перехода 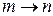в момент t. Из (6.38) получаем

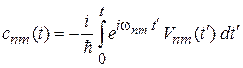. (6.39)

Правый индекс m соответствует начальному состоянию, левый – конечному.

Вероятность перехода 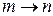, т. е. вероятность обнаружения системы в состоянии n, если при 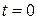было состояние 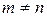, находим из (6.39)

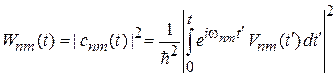. (6.40)

Состояние при 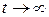. По истечении большого промежутка времени интегрирование в (6.39) можно провести в бесконечных пределах

– коэффициент перехода 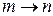при 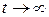пропорционален Фурье-образу возмущения 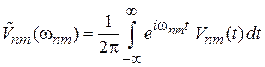на частоте перехода.

Частные случаи:

а) Постоянное возмущение 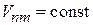дает

.

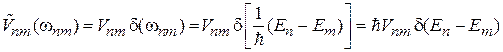Выполняется закон сохранения энергии, переходы происходят между вырожденными состояниями.

б) Адиабатическое возмущение соответствует матричному элементу 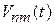, слабо изменяющемуся за время 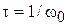, тогда по теореме о частотной полосе 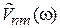– мало при 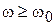и существенны переходы с низкими частотами .

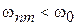Периодическое возмущение с частотой w, действующее при :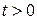

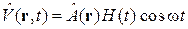
дает коэффициент перехода (6.39)

,

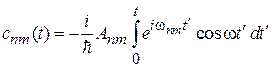где 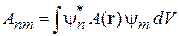. По формуле Эйлера получаем

.

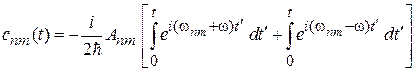Для частоты возмущения w, близкой к частоте перехода 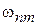, второй интеграл, равный 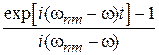, гораздо больше первого, тогда

.

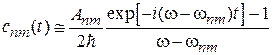Используя

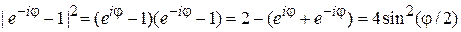
и вводя частоту отстройки 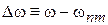, находим вероятность перехода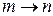

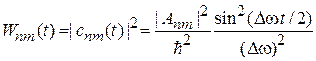. (6.41)

Вероятность перехода за единицу времени

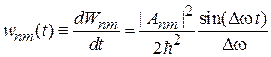. (6.42)

При 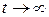с учетом 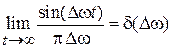, из (6.42) находим

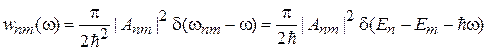. (6.43)

Дельта-функция обеспечивает выполнение закона сохранения энергии 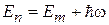. Переход 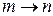совершается, если частота возмущения w равна частоте перехода 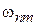и система получает энергию квантом 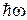, как показано на рис. 1.

Для переходов в квазинепрерывном спектре из состояния m в интервал состояний 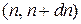, из (6.43) получаем

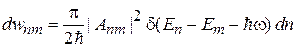. (6.44)

Date: 2015-05-19; view: 524; Нарушение авторских прав