ПРИМЕРЫ. 11.3. Получить оператор проекции спина на направление, заданное векторомn

11.3. Получить оператор проекции спина 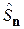на направление, заданное вектором n. Найти собственные функции и собственные значения оператора в сферической системе координат.

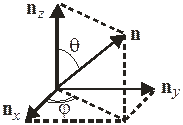
Декартовы компоненты единичного вектора n, заданного углами 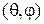сферической системы координат:

, , .

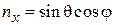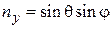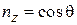Используя

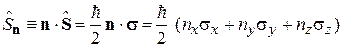
и (7.10), находим оператор проекции спина на направление, заданное углами θ и φ:

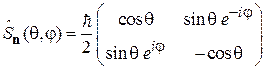. (П.11.6)

Собственная функция 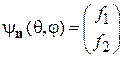удовлетворяет 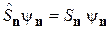. Подставляя функцию и (П.11.6), получаем систему уравнений

.

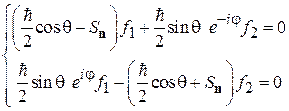Условие совместности

дает собственные значения 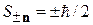, совпадающие с (7.4). Проекция спина на любое направление одинакова и равна .

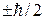Функция 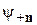с собственным значением 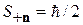удовлетворяет уравнению 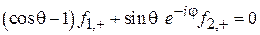, или

.

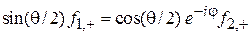Находим решение

, , .

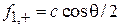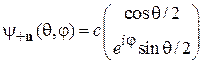Нормировка (7.13) дает 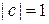, тогда с точностью до постоянного фазового множителя

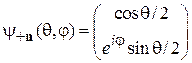. (П.11.7)

Для собственного значения 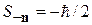в (П.11.7) заменяем 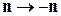, , 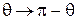, 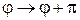и получаем

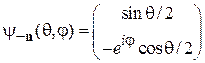. (П.11.8)

Выполняются условия нормировки (7.13) и ортогональности (7.14)

, .

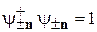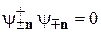При 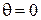, 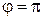вектор n направлен по оси z и для оператора 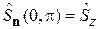из (П.11.7) и (П.11.8) получаем собственные функци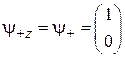и и 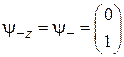, совпадающие с (7.16).

При 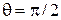, 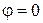вектор n направлен по оси x. Из (П.11.7) и (П.11.8) находим для оператора 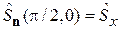собственные функции

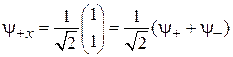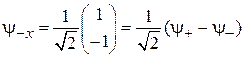, . (П.11.9)

При 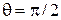, 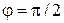вектор n направлен по оси y. Из (П.11.7) и (П.11.8) для оператора получаем

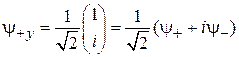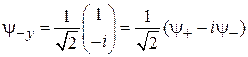, . (П.11.10)

11.5. Найти спиновые функции двухэлектронных состояний 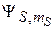с определенными значениями полного спина S и проекции .

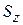Если спины электронов направлены вдоль оси z, то 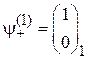, , 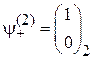двухчастичное состояние имеет спиновые числа 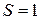, 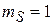и описывается функцией

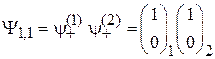. (П.11.14)

Для состояния 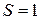, 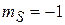получаем

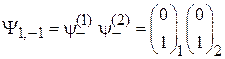. (П.11.15)

Состояние 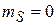возникает, если проекции спина частиц имеют противоположные знаки:

.

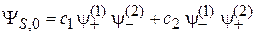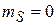Для состояния и находим коэффициенты с ₁ и с ₂ из уравнения (7.8) в виде

,

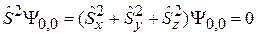тогда

, , .

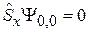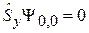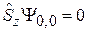Учитывая 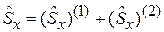, получаем:

.

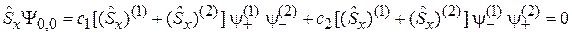Операторы с индексом действуют на функции с тем же индексом. Используя результат задачи 4.23 в виде

,

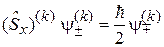находим

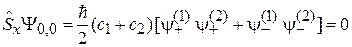
и получаем 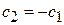. Уравнения 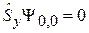и 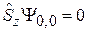дают тот же результат. Из условия нормировки (7.13) 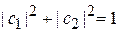находим 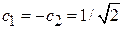и получаем

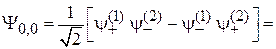
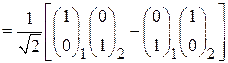. (П.11.16)

Следовательно, спиновая функция двухчастичного состояния антисимметрична при перестановке частиц.

Для состояния

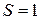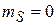с и находим коэффициенты из условия ортогональности 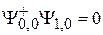состоянию (П.11.16). Учитывая (7.16) 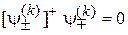, , 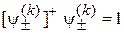получаем 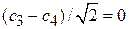, тогда ,

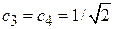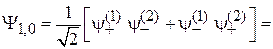
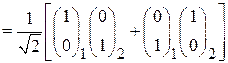. (П.11.17)

Из (П.11.14), (П.11.15) и (П.11.17) следует, что спиновые функции двухчастичных состояний 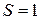симметричны при перестановке частиц.

Состояние

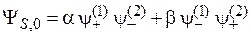(П.11.18)

называется перепутанным по спинам двух частиц. Функция (П.11.18) не представима в виде произведения функций одночастичных состояний. Термин «перепутанное состояние» ввел Э. Шредингер в 1935 г. В состоянии (П.11.18) частицы 1 и 2 находятся в разных местах, имеют неопределенные проекции спина, при этом проекция полного спина равна нулю. Частицы взаимно коррелированны, – если у частицы 1 измерить проекцию спина на произвольное направление, то, как следует из примера 11.3, возможные результаты 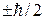. Тогда у частицы 2 состояние изменяется – проекция на то же направление становится определенной – 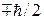. Частицы могут находиться на произвольно большом расстоянии друг от друга и такое преобразование состояния частицы 2 без прямого воздействия на нее означает нелокальность перепутанного состояния. Этот результат получили Альберт Эйнштейн, Борис Подольский и Натан Розен в 1935 г. и рассматривали его как парадокс, опровергающий квантовую механику. Однако, нелокальность перепутанного состояния подтверждена многочисленными экспериментами, при этом передача информации со сверхсветовой скоростью невозможна. Получают перепутанное по координате, импульсу или спину состояние двух частиц путем распада частицы или системы, находящейся в определенном по этим параметрам состоянии.

Функция (П.11.18) с условием нормировки 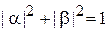образует суперпозицию 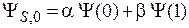экспериментально различимых состояний

,

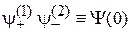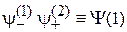
и является квантовой единицей информации – кубитом (qubit от англ. quantum bit – «квантовый бит»). Термин ввел в 1995 г. Бен Шумахер. В отличие от бита, принимающего значения 0 или 1, кубит 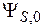несет значение 0 с вероятностью 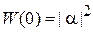и значение 1 с вероятностью 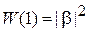. Поэтому кубит содержит информацию в несопоставимо большем объеме, чем бит. Кубиты используются в квантовом компьютере для хранения и преобразования информации.

Date: 2015-05-19; view: 2031; Нарушение авторских прав