
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ошибка! Ошибка связи
|
|
Анализатор Штерна–Герлаха
Противоречие с теорией устранили в 1925 г. Дж. Уленбек и С. Гаудсмит, введя спин электрона и связанный с ним магнитный момент. По углу θ были вычислены проекции магнитного момента электрона
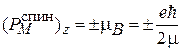 . (7.3)
. (7.3)
Опыт Штерна–Герлаха дает два спиновых состояния электрона. Исходя из аналогии спина s с орбитальным моментом l, получаем 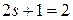 , тогда спиновые квантовые числа s и
, тогда спиновые квантовые числа s и 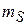 , спиновый момент
, спиновый момент 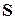 и его проекция
и его проекция 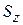 равны
равны
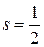 ,
, 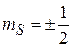 ,
, 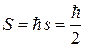 ,
, 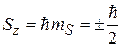 . (7.4)
. (7.4)
Спиновый магнитный момент электрона (7.3) выражается через спин
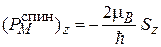 ,
, 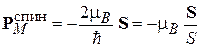 . (7.5)
. (7.5)
Знак «–» связан с отрицательным зарядом электрона. Полный магнитный момент электрона складывается из орбитального (7.1) и спинового (7.5) моментов
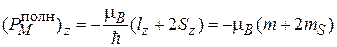 . (7.6)
. (7.6)
Операторы спина вводятся по аналогии с операторами момента импульса
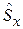 ,
, 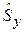 ,
, 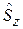 ,
, 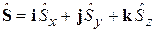 ,
, 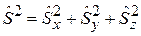 ,
,
и удовлетворяют соотношениям, аналогичным (4.5):
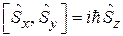 ,
, 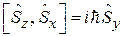 ,
,
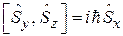 ,
, 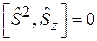 . (7.7)
. (7.7)
Поскольку спин не выражается через координату и импульс, то 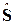 коммутирует с
коммутирует с 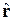 и
и 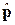 . Уравнения для собственных функций операторов спина аналогичны (4.14)–(4.15)
. Уравнения для собственных функций операторов спина аналогичны (4.14)–(4.15)
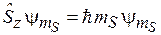 ,
,
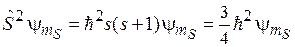 . (7.8)
. (7.8)
Матрицы Паули. В набор квантовых чисел электрона в атоме кроме n, l, m входит спиновое число 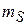 , тогда функция состояния
, тогда функция состояния
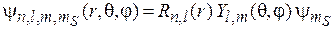 .
.
Поскольку 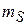 двузначная величина, то считаем
двузначная величина, то считаем 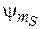 двухэлементной матрицей
двухэлементной матрицей 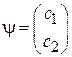 – спинором, тогда операторы спина получают матричную форму
– спинором, тогда операторы спина получают матричную форму
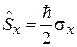 ,
, 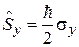 ,
, 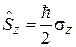 ,
, 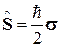 . (7.9)
. (7.9)
Матрицы Паули
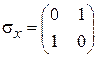 ,
, 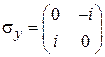 ,
, 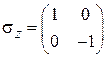 ,
, 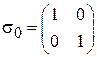 (7.10)
(7.10)
удовлетворяют соотношениям
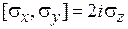 ,
, 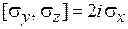 ,
, 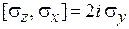 ,
,
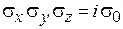 ,
, 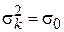 ,
, 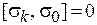 ,
,
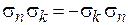 ,
, 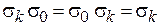 ,
, 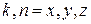 ;
; 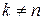 ,
,
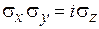 ,
, 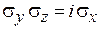 ,
, 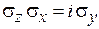 , (7.11)
, (7.11)
что обеспечивает выполнение (7.7). Из (7.9) – (7.11) получаем
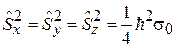 ,
, 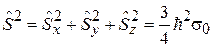 ,
,
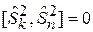 ,
, 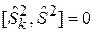 .
.
Эрмитово сопряжение матрицы включает комплексное сопряжение * и транспонирование T ее элементов
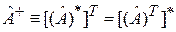 . (7.12)
. (7.12)
Используя (7.9) и (7.10) получаем, что операторы спина и матрицы Паули эрмитовые, например
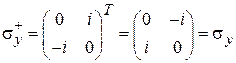 .
.
Нормировка и ортогональность спиноров 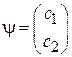 и
и 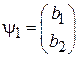 имеют вид
имеют вид
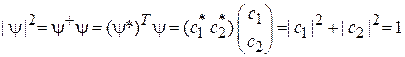 , (7.13)
, (7.13)
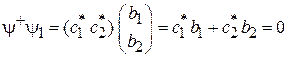 . (7.14)
. (7.14)
Среднее значение проекции k спина по нормированному состоянию y определяется в виде
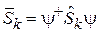 . (7.15)
. (7.15)
Собственные функции оператора 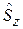 удовлетворяют уравнению
удовлетворяют уравнению
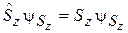 .
.
Решение ищем в виде 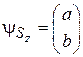 . Подстановка в уравнение дает
. Подстановка в уравнение дает
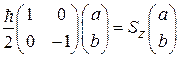 ,
, 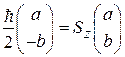 .
.
Сравнивая элементы матриц, получаем систему алгебраических уравнений
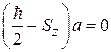 ,
, 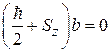 .
.
Если 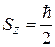 , то
, то 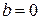 и
и 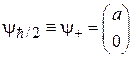 ; если
; если 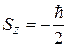 , то
, то 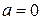 и
и 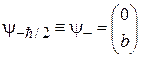 . Из условия нормировки (7.13) с точностью до фазового множителя получаем для оператора
. Из условия нормировки (7.13) с точностью до фазового множителя получаем для оператора 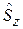 собственные функции
собственные функции
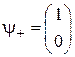 ,
, 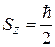 ;
; 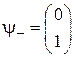 ,
, 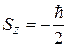 ;
;
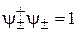 ,
, 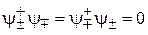 , (7.16)
, (7.16)
взаимно ортогональные и образующие полный ортонормированный базис. Произвольное спиновое состояние разлагается по базису
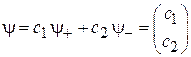 ,
, 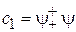 ,
, 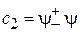 . (7.17)
. (7.17)
Вероятности обнаружения проекций спина 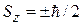 равны
равны
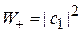 ,
, 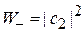 . (7.18)
. (7.18)
Свободный электрон со спином, направленным по оси z, с энергией Е и импульсом р описывается спинором
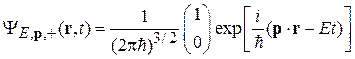 . (7.19)
. (7.19)
Date: 2015-05-19; view: 697; Нарушение авторских прав