ПРИМЕРЫ. 9.3.На одномерную двухуровневую стационарную систему действует возмущение, зависящее от времени

9.3. На одномерную двухуровневую стационарную систему действует возмущение, зависящее от времени. Описать состояние системы, не используя приближенных методов.

Невозмущенные состояния 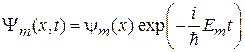, где 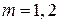, удовлетворяют

, .

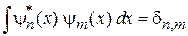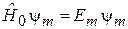Решение уравнения с возмущением

ищем в виде суперпозиции невозмущенных состояний

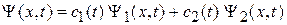. (П.9.2)

Подстановка (П.9.2) в уравнение дает

.

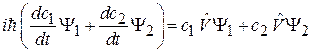Умножая равенство на y₁, или на y₂, интегрируя по пространству и учитывая условие ортонормированности, получаем уравнения для коэффициентов

,

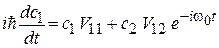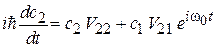, (П.9.3)

где 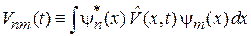, – частота перехода.

9.4. На двухуровневую систему в состоянии 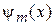, где 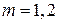; 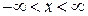, действует периодическое возмущение 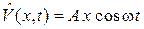с частотой w, близкой к частоте перехода . Таким возмущением является гармоническая электромагнитная волна, действующая на систему с дипольным моментом ex. Найти возмущенное состояние системы.

Матричные элементы возмущения

, ,

, , .

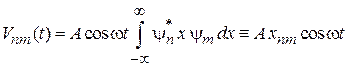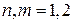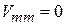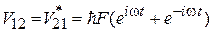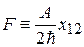Из (П.9.3) получаем

,

.

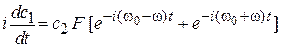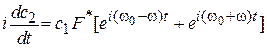Вблизи резонанса 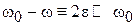, где e – частота отстройки, для атомных переходов выполняется 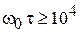, где t – характерное время жизни состояния. Тогда 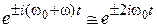осциллирует с высокой частотой около нуля и этим вкладом можно пренебречь. Уравнения получают вид

, .

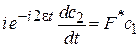Замена 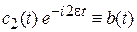с учетом преобразует уравнения к виду

, .

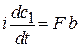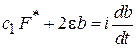Дифференцируя последнее равенство и исключая с ₁, получаем

.

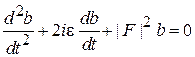Решение ищем в виде

.

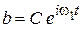Это дает уравнение

,

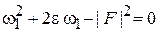откуда находим

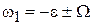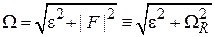, , (П.9.4)

где 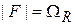– частота Раби. В результате

, ,

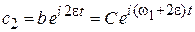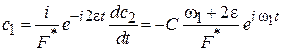тогда

, .

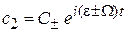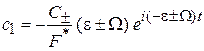Из (П.9.2) получаем общее решение

+ .

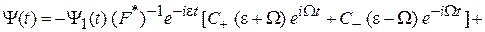
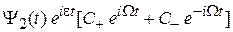Если при 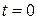система находилась на уровне 1, тогда

,

.

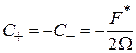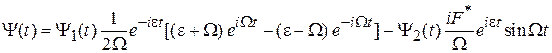Квадрат модуля коэффициента при Y₂ дает вероятность нахождения частицы на уровне 2

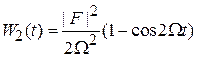. (П.9.5)

С учетом (П.9.4) находим

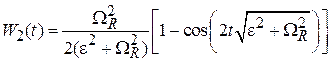. (П.9.6)

При точном резонансе 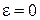получаем

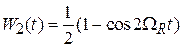. (П.9.7)

При совпадении частоты возмущения w с частотой перехода w₀ система периодически переходит между уровнями с частотой Раби

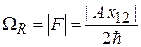. (П.9.8)

Время перехода между уровнями 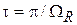уменьшается с увеличением энергии возмущения, что согласуется с соотношением неопределенностей время-энергия. При большой частоте отстройки 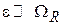вероятность нахождения частицы на уровне 2

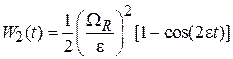(П.9.9)

– мала и осциллирует с частотой отстройки. Исидор Айзек Раби (1898–1988) разработал в 1937 г. метод магнитного резонанса для измерения магнитного момента у частиц в молекулярном пучке.

Date: 2015-05-19; view: 369; Нарушение авторских прав