Уравнение Паули

Спиновый магнитный момент электрона

,

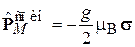где 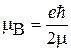– магнетон Бора; g – множитель Ланде, взаимодействует с магнитным полем В и создает дополнительный вклад в гамильтониан

.

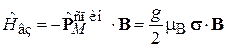В результате уравнение Шредингера переходит в уравнение, полученное Вольфгангом Паули в 1927 г.

Гамильтониан электрона без учета спина в поле с векторным потенциалом А имеет вид

.

С учетом спина получаем гамильтониан в матричной форме

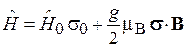, (7.20)

где

,

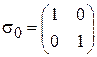. (7.21)

Подставляем (7.20) в уравнение Шредингера

,

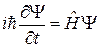и получаем уравнение Паули

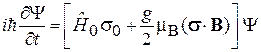, (7.22)

где 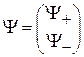; 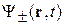– состояния с проекциями спина 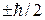на ось z.

Однородное поле В. Слагаемое 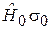в (7.22) не зависит от спина, а 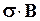не зависит от координат, поэтому спиновые и координатные переменные разделяются

,

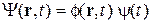где 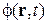– координатная функция,

– спиновая функция;

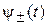– состояния с проекциями спина 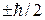на ось z. Делим (7.22) слева на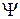

,

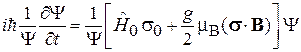подставляем 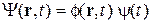, и получаем

.

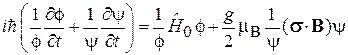Координатная и спиновая функции разделяются, получаем независимые уравнения

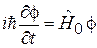, (7.23)

. (7.24)

Взаимодействие спина с однородным магнитным полем не влияет на координатную часть волновой функции .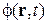

При 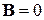спиновая функция не зависит от времени.

При 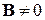используем (7.21)

, .

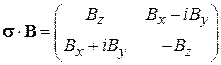Для спиновых функций 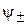с противоположными проекциями спина на ось z из (7.24) получаем

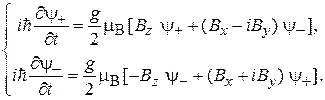(7.25)

Направляем ось z вдоль поля, тогда 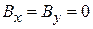, 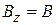и уравнения разделяются

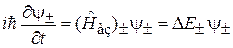, (7.26)

где

;

.

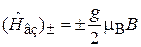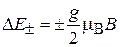Стационарное состояние. Если магнитное поле В и потенциальная энергия U не зависят от времени, тогда из (7.23) и (7.26) следует, что состояния

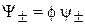
удовлетворяют стационарному уравнению Шредингера

.

Учитывая

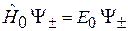
и (7.26), получаем

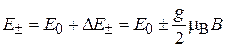. (7.27)

Если спин электрона направлен по полю, то его спиновый магнитный момент – против поля и энергия состояния увеличивается на .Если спин направлен против поля, то магнитный момент – по полю и энергия состояния понижается на . Магнитное поле расщепляет уровень энергии, снимая вырождение по спиновому числу 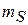. Расщепление в магнитном поле уровней атома с разными значениями магнитного квантового числа и нулевым спином исследовал П. Зееман в 1896 г. Спиновое расщепление

называется аномальным эффектом Зеемана. Его описал А. Ланде в 1922 г.

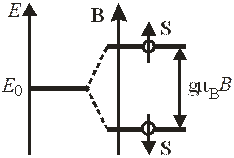
Спиновое расщепление уровня

Питер Зееман Альфред Ланде

(1865–1943) (1888–1976)

Решения уравнения (7.26) для спиновых функций

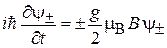
имеют вид

,

,

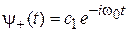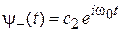где

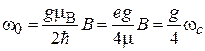; (7.28)

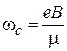– циклотронная частота. Получаем спиновую функцию

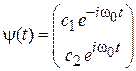(7.29)

с условием нормировки

.

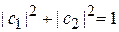Находим средние проекции спина (7.15)

,

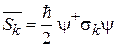где

, , .

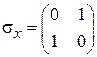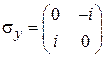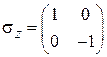Получаем

,

,

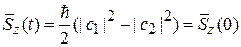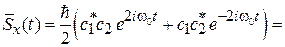
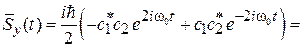
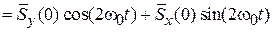, (7.30)

где

, .

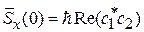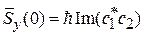В постоянном магнитном поле сохраняется средняя проекция спина электрона на направление поля, вектор спина вращается вокруг направления поля с частотой .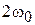

При 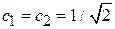вектор спина находится в плоскости (x, y), в начальный момент направлен вдоль оси x, с течение времени вращается вокруг оси z по часовой стрелки, если смотреть вдоль вектора магнитного поля, частота прецессии при равна циклотронной частоте. Вектор спина дырки, имеющей положительный заряд, вращается в противоположную сторону. При 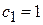, 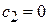спин направлен вдоль магнитного поля, вращение отсутствует.

Спиновые магнитные переходы. Взаимодействие спинового магнитного момента электрона с магнитным полем расщепляет уровень энергии на два подуровня. Ранее было показано, что периодическое возмущение двухуровневой системы вызывает переходы между уровнями с частотой Раби.

Рассмотрим действие на электрон полупроводника двух однородных магнитных полей. Постоянное поле В, направленное по оси z:

,

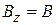расщепляет уровень энергии. Поле 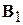, вращающееся в плоскости (x,y) с частотой w:

, ,

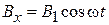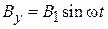позволяют управлять спиновым состоянием, т. е. получать желаемую проекцию спина на ось z, измерять магнитный момент и эффективную массу частицы.

Компоненты спиновой функции электрона

удовлетворяют системе уравнений (7.25)

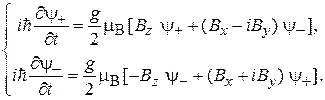
Для рассматриваемой системы

,

,

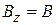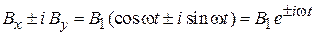получаем

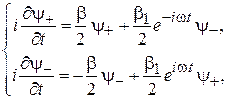(7.31)

где

;

.

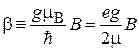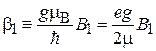Заменяем

,

,

.

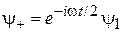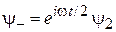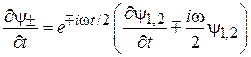Уравнения (7.31) получают вид

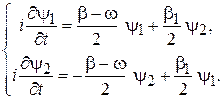(7.32)

Общие решения ищем в виде

,

.

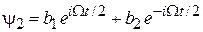Подставляем решения в (7.32). Второе уравнение выполняется при любом t, если

,

.

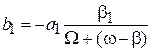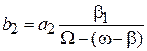Первое уравнение удовлетворяется при любом t для частоты Раби

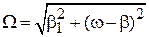. (7.33)

В результате

,

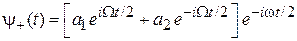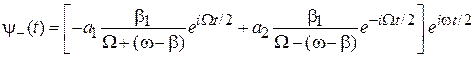. (7.34)

Пусть при 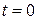спин направлен против оси z, тогда

,

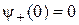и из (7.34) находим

.

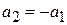Условие нормировки

дает

,

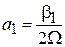тогда

. (7.35)

Вероятность перевернутого спина равна

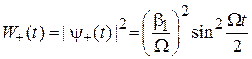. (7.36)

Через время

спин переворачивается. Проекция спина на направление постоянного магнитного поля периодически изменяется с частотой Раби. Измерив период осцилляций 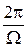, находим частоту Раби (7.33)

,

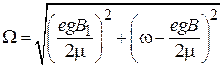и вычисляем . Выключая в определенный момент времени, получаем желаемую проекцию спина на ось z.

Циклотронный резонанс. Пусть при 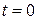спин электрона направлен в противоположную сторону по отношению к полю В и электрон находится в основном состоянии. Поле В ₁ слабое

, ,

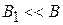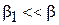и осциллирует с высокой частотой

.

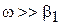С учетом

,

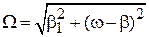вероятность переворота спина (7.36)

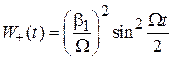
мала для всех частот ω за исключением резонансной частоты

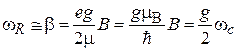. (8.37)

При этом частота Раби

,

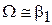и вероятность переворота спина

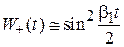
достигает единицы. На перевороты спина тратится энергия переменного магнитного поля. Измерив частоту поля 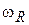, при которой происходит наибольшее поглощение энергии, по формуле (8.37) находим эффективную массу, деленную на фактор Ланде. Длина электромагнитной волны, вызывающей резонанс системы с , в поле , находится в СВЧ диапазоне

.

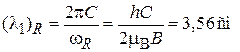При резонансная частота (8.37) совпадает с циклотронной частотой 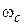, поэтому такое явление называется циклотронный резонанс. Выбирая направление вращения поля 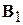можно избирательно воздействовать на электроны, или на дырки полупроводника. Метод циклотронного резонанса широко используется для изучения зонной структуры полупроводников и процессов рассеяния носителей тока.

Использование атома со спином вместо электрона позволяет применить рассмотренный метод для исследования парамагнетиков. Впервые это сделал Евгений Константинович Завойский в 1944 г. Метод называется электронный парамагнитный резонанс.

Date: 2015-05-19; view: 778; Нарушение авторских прав