Волновые свойства света

Свет – электромагнитная волна.

Магнитная составляющая не влияет на заряды, движущиеся со скоростями, гораздо меньшими скорости света. Волну характеризуем электрической составляющей A (x,t). Если поляризация несущественна, то плоская гармоническая волна вдоль оси x

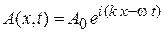, (1.1)

где А ₀ – амплитуда; 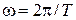– круговая частота, Т – период колебаний; 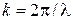– волновое число, λ – длина волны.

Плотность энергии – усредненная по времени энергия единицы объема

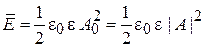. (1.2)

Интерференция – перераспределение энергии при наложении когерентных волн. Пусть гармоническая волна разделяется на две волны, которые проходят пути x ₁ и x ₂ до области наложения волн. Амплитуда суммарного колебания зависит от разности хода .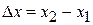

Максимум интерференции

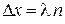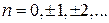, (1.3)

– смещения в складывающихся волнах происходят в фазе, результирующая амплитуда удваивается, плотность энергии (1.2) учетверяется.

Минимум интерференции

,

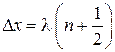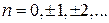
– приходящие волны колеблются в противофазе, результирующая амплитуда и плотность энергии равны нулю.

Дифракция – отклонение волны от прямолинейного распространения, вызванное ограничением волновой поверхности.

На экран со щелью шириной 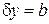падает плоская волна. До экрана проекции волнового вектора и неопределенности положения и волнового вектора по оси y равны

, , , .

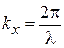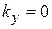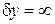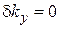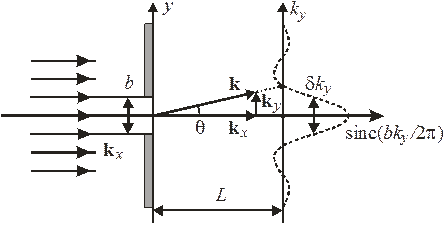
Рис. 1.1. Дифракция на щели

После щели амплитуда волны относительно оси y описывается прямоугольной функцией 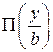. Ее спектр, т. е. Фурье-образ:

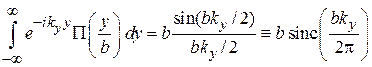
содержит существенный вклад волнового вектора в интервале

.

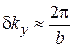Следовательно, волна дифрагирует в пределах угла

.

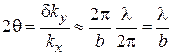Чем уже щель, тем сильнее дифракция. При малой длине волны 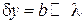получаем 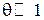– дифракция несущественна и свет проявляет корпускулярные свойства.

Соотношения неопределенностей. После экрана

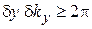. (1.4)

Используя 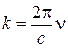, где ν – частота волны; c – скорость света, находим 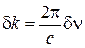, 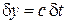и из (1.4) получаем

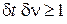(1.5)

– теорема Фурье о частотной полосе.

Date: 2015-05-19; view: 356; Нарушение авторских прав